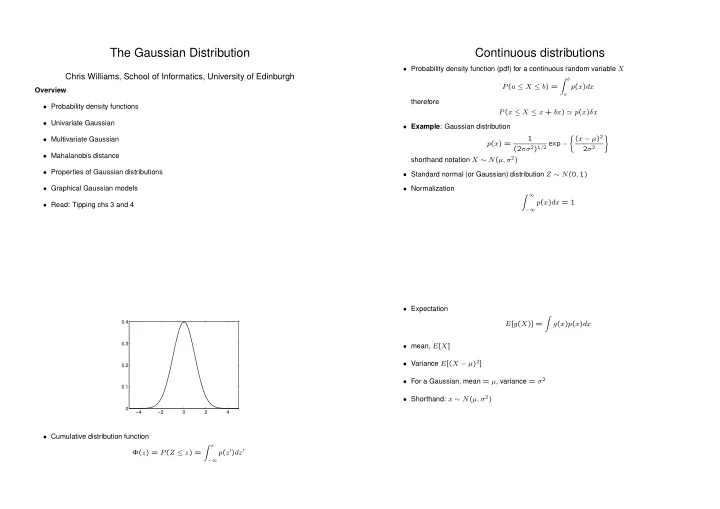
The Gaussian Distribution Continuous distributions Probability - PowerPoint PPT Presentation

The Gaussian Distribution Continuous distributions • Probability density function (pdf) for a continuous random variable X Chris Williams, School of Informatics, University of Edinburgh � b P ( a ≤ X ≤ b ) = p ( x ) dx Overview a therefore • Probability density functions P ( x ≤ X ≤ x + δx ) ≃ p ( x ) δx • Univariate Gaussian • Example : Gaussian distribution � ( x − µ ) 2 � 1 • Multivariate Gaussian p ( x ) = (2 πσ 2 ) 1 / 2 exp − 2 σ 2 • Mahalanobis distance shorthand notation X ∼ N ( µ, σ 2 ) • Properties of Gaussian distributions • Standard normal (or Gaussian) distribution Z ∼ N (0 , 1) • Graphical Gaussian models • Normalization � ∞ p ( x ) dx = 1 • Read: Tipping chs 3 and 4 −∞ • Expectation � 0.4 E [ g ( X )] = g ( x ) p ( x ) dx 0.3 • mean, E [ X ] • Variance E [( X − µ ) 2 ] 0.2 • For a Gaussian, mean = µ , variance = σ 2 0.1 • Shorthand: x ∼ N ( µ, σ 2 ) 0 −4 −2 0 2 4 • Cumulative distribution function � z p ( z ′ ) dz ′ Φ( z ) = P ( Z ≤ z ) = −∞

Bivariate Gaussian I • Let X 1 ∼ N ( µ 1 , σ 2 1 ) and X 2 ∼ N ( µ 2 , σ 2 2 ) 1 0.8 • If X 1 and X 2 are independent 0.6 0.4 � ( x 1 − µ 1 ) 2 + ( x 2 − µ 2 ) 2 � 1 2 ) 1 / 2 exp − 1 p ( x 1 , x 2 ) = 0.2 2 π ( σ 2 1 σ 2 σ 2 σ 2 2 1 2 0 2 1 2 1 0 0 −1 −1 � � � � � σ 2 � −2 x 1 µ 1 0 −2 • Let x = , µ = , Σ = 1 σ 2 x 2 µ 2 0 2 2 π | Σ | 1 / 2 exp − 1 1 � ( x − µ ) T Σ − 1 ( x − µ ) � p ( x ) = 2 Bivariate Gaussian II Multivariate Gaussian • Covariance • P ( x ∈ R ) = � R p ( x ) d x • Σ is the covariance matrix Σ = E [( x − µ )( x − µ ) T ] • Multivariate Gaussian Σ ij = E [( x i − µ i )( x j − µ j )] � � 1 − 1 2( x − µ ) T Σ − 1 ( x − µ ) p ( x ) = (2 π ) d/ 2 | Σ | 1 / 2 exp • Example: plot of weight vs height for a population • Σ is the covariance matrix Σ = E [( x − µ )( x − µ ) T ] Σ ij = E [( x i − µ i )( x j − µ j )]

Mahalanobis Distance • Σ is symmetric d 2 Σ ( x i , x j ) = ( x i − x j ) T Σ − 1 ( x i − x j ) • Shorthand x ∼ N ( µ , Σ) • d 2 Σ ( x i , x j ) is called the Mahalanobis distance between x i and x j • If Σ is diagonal, the contours of d 2 Σ are axis-aligned ellipsoids • For p ( x ) to be a density, Σ must be positive definite • If Σ is not diagonal, the contours of d 2 Σ are rotated ellipsoids Σ = U Λ U T • Σ has d ( d + 1) / 2 parameters, the mean has a further d where Λ is diagonal and U is a rotation matrix • Σ is positive definite ⇒ entries in Λ are positive Parameterization of the covariance matrix Transformations of Gaussian variables • Linear transformations of Gaussian RVs are Gaussian • Fully general Σ = ⇒ variables are correlated X ∼ N ( µ x , Σ) Y = A X + b • Spherical or isotropic. Σ = σ 2 I . Variables are independent Y ∼ N ( A µ x + b , A Σ A T ) • Sums of Gaussian RVs are Gaussian • Diagonal [Σ] ij = δ ij σ 2 i Variables are independent Z = X + Y E [ Z ] = E [ X ] + E [ Y ] • Rank-constrained: Σ = WW T + Ψ , with W being a d × q matrix with var[ Z ] = var[ X ] + var[ Y ] + 2covar[ XY ] q < d − 1 and Ψ diagonal. This is the factor analysis model. If Ψ = σ 2 I , if X and Y are independent var[ Z ] = var[ X ] + var[ Y ] then with have the probabilistic principal components analysis (PPCA) model

Properties of the Gaussian distribution Graphical Gaussian Models • Gaussian has relatively simple analytical properties Example: • Central limit theorem. Sum (or mean) of M independent random variables is distributed normally as M → ∞ (subject to a few general conditions) x • Diagonalization of covariance matrix = ⇒ rotated variables are independent • All marginal and conditional densities of a Gaussian are Gaussian • The Gaussian is the distribution that maximizes the entropy H = − � p ( x ) log p ( x ) d x y z for fixed mean and covariance • Let X denote pulse rate • Let Y denote measurement taken by machine 1, and Z denote measurement taken by machine 2 As before • Model X ∼ N ( µ x , v x ) P ( x, y, z ) = P ( x ) P ( y | x ) P ( z | x ) Y = µ y + w y ( X − µ x ) + N y Z = µ z + w z ( X − µ x ) + N z Show that noise N y ∼ N (0 , v N y ) , N z ∼ N (0 , v N z ) , independent • ( X, Y, Z ) is jointly Gaussian; can do inference for X given Y = y and Z = z   µ x µ = µ y     µ z  v x w y v x w z v x  w 2 y v x + v N w y v x w y w z v x Σ =   y   w 2 z v x + v N w z v x w y w z v x z

Inference in Gaussian models Hybrid (discrete + continuous) networks • Partition variables into two groups, X 1 and X 2 � � • Could discretize continuous variables, but this is ugly, and gives large µ 1 µ = µ 2 CPTs � � Σ 11 Σ 12 Σ = Σ 21 Σ 22 • Better to use parametric families, e.g. Gaussian µ c 1 | 2 = µ 1 + Σ 12 Σ − 1 22 ( x 2 − µ 2 ) Σ c 1 | 2 = Σ 11 − Σ 12 Σ − 1 • Works easily when continuous nodes are children of discrete nodes; we 22 Σ 21 then obtain a conditional Gaussian model • For proof see § 13.4 of Jordan (not examinable) • Formation of joint Gaussian is analogous to formation of joint probability table for discrete RVs. Propagation schemes are also possible for Gaussian RVs