Study of the spin orbit force using a bubble nucleus O. Sorlin - PowerPoint PPT Presentation

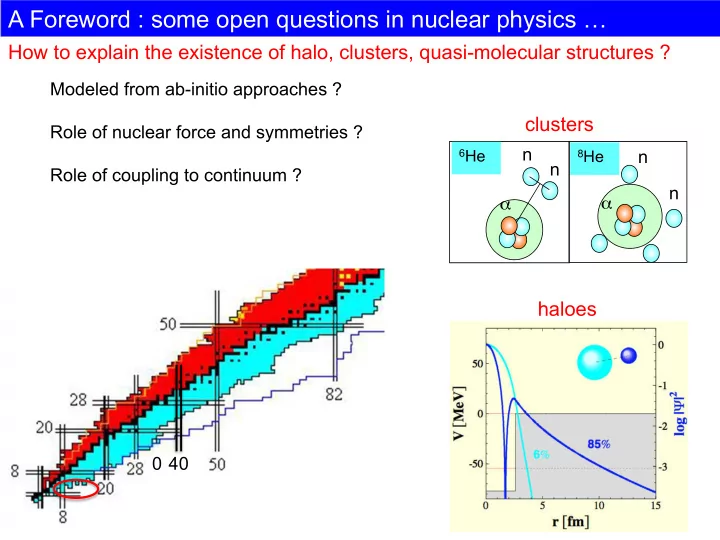
A Foreword : some open questions in nuclear physics … How to explain the existence of halo, clusters, quasi-molecular structures ? Modeled from ab-initio approaches ? clusters Role of nuclear force and symmetries ? n 6 He n 8 He n Role of coupling to continuum ? n α α haloes 0 40

A Foreword : some open questions in nuclear physics … 3500 8 O 2000 3000 6000 E(2 + ) (keV) 2500 1500 28 Ni 4000 2000 6 C 1000 20 Ca 1500 14 Si 2000 1000 16 S 500 500 0 0 0 4 6 8 10 12 12 16 20 24 32 36 40 44 Neutron Number Neutron Number Neutron Number Do magic nuclei persist far off stab.? -> pillars of nuclear structure -> remarkable properties due to shell gaps (i.e. large first excited state energy) 40

A Foreword : some open questions in nuclear physics … 3500 2000 3000 6000 E(2 + ) (keV) 2500 1500 4000 2000 24 Cr 1000 1500 4 Be 26 Fe 2000 1000 10 Ne 500 12 Mg 500 0 0 0 4 6 8 10 12 12 16 20 24 32 36 40 44 Neutron Number Neutron Number Neutron Number If our world were more neutron-rich … . ->No sign of energy increase -> No magic number far from stability ! -> Change of paradigm … . 40

A Foreword : some open questions in nuclear physics … 3500 8 O 2000 3000 6000 E(2 + ) (keV) 2500 1500 28 Ni 8 O 4000 2000 6 C 24 Cr 1000 20 Ca 1500 14 Si 4 Be 26 Fe 2000 1000 16 S 10 Ne 500 12 Mg 500 0 0 0 4 6 8 10 12 12 16 20 24 32 36 40 44 Neutron Number Neutron Number Neutron Number If our world would be more neutron-rich … . ->No sign of energy increase -> No magic number far from stability ! -> Change of paradigm … . Why ? Which part(s) of nuclear force ? 40 Are there new magic nuclei ? What happens to heavier nuclei ?

A Foreword : some open questions in nuclear physics … Z=120 Does an island of extra-stability exist for superheavy nuclei ? Could we predict its location ? Could we synthesize new elements on earth ? Which chemical properties ?

A Foreword : some open questions in nuclear physics … Which stellar environment(s) produce elements Z>26? r-abundance curve Neutron star mergers ? Likely but … . Link between closed shells and abundance peaks -> A real impact of shell structure far from stability Solar observation -> Determine mass, lifetime, n-capture rates of nuclei Shell closure Shell quenching A r process D. Price & S. Rosswog Science 2006

Study of the spin orbit force using a bubble nucleus O. Sorlin (GANIL, presently at CERN) THE PITCH The spin orbit (SO) force plays major role ℓ in nuclear structure to create shell gaps s Shell gap ℓ ,s that give rise to magic nuclei. s ℓ SO force: postulated more than 60 years ago. Theoretical descriptions now exist but predictions differ for ab-normal nuclei No experiment was yet able to test the SO force in ‘extreme’ conditions (superheavy elements, nuclear drip-line -> astrophysics) ρ p (r) 34 Si We propose to use a ‘bubble’ nucleus to test the properties of this SO force Mardi 26 avril 2016 – LAL Orsay

Layout of the talk Introduction on the atomic nucleus -> Charge density, orbital occupancies Probe charge density in 36 S and 34 Si:knockout reactions at NSCL -> Central proton density depletion in 34 Si (i.e. bubble) Introduction to the spin orbit (SO) force ‘ May the force be with you ’ -> Properties and expectations Obi-Wan Kenobi ‘ Star Wars ’ -> Use a bubble nucleus to constrain unknown properties Reduced SO interaction between 36 S & 34 Si: (d,p) reaction at GANIL Conclusions / consequences

Charge density of the nucleus : ρ (r) Large transferred momentum -> details of the density distribution 208 Pb T e ≈ hc/ λ e- ρ (r) A B r

Charge density of the nucleus : ρ (r) Saturation of nuclear forces ρ (r) 208 Pb scaling with A 1/3 7 142 Nb (5/3<r 2 >) 1/2 124 Sn 6 92 Mo 96 Zr 58 Ni 5 52 Cr 40 Ca 58 Ni 4 R=r 0 A 1/3 16 O ρ (r) 3 5 6 A 1/3 4 Halo nucleus 12 C Z 4 He Hofstader Rev. Mod. Phys. 28 (1956)

Charge density depletion in the center of the 205 Tl nucleus Δρ (r) 0.08 (e fm -3 ) MF 206 Pb ρ [fm -3 ] 0.08 0.06 Cavedon PRL (1982) 205 Tl 3s 1/2 0.04 0.04 r[fm] 0.02 0 r (fm) 4 8 0 6 8 2 2 4 6 r[fm] Charge density depletion due to the change in 3s 1/2 occupancy by 0.7 proton Independent particle model works rather well also in the interior of nucleus ρ (r) L=0,1,2,3 n=0,1… Nuclear density = superposition of radial vave funtions with n,L values r

Probing nuclear orbits with (e,e ’ p) reaction N p Orbital labelling n,L,J 82 s 1/2 n nodes (n=0,1,2) d 3/2 h 11/2 L angular momentum d 5/2 E * [MeV] E p [MeV] (s,p,d,f,g,h … ) g 7/2 50 (-1) L parity 82 Pb |L-s|<J<|L+s| Nuclear orbits (2J+1) per shell example : ->Nucleons are arranged on shells h 11/2 : L=5, J=11/2, -> Gaps are present for certain nucleon numbers L and s aligned -> N p detected follows orbit occupancy contains 12 nucleons -> Quenching factor of occupancy by about 70% -> Mixing with collective states at high E* -> Study limited (so far) to STABLE nuclei

Proton density deple6on in 34 Si as compared to 36 S? E ρ p (r) 36 S 20 36 S 1d 3/2 0 ? 2s 1/2 2 14 1d 5/2 6 0 1 u 2 Proton orbits occup. E 34 Si 20 ρ p (r) 34 Si 0 1d 3/2 2s 1/2 0 14 ? 1d 5/2 6 0 1 u 2 Proton orbits occup. J.P. Ebran DDME2 interaction Amplitude of the central depletion depends on the change in 2s 1/2 occupancy But correlations can reduce the amplitude of this depletion

Probing proton density in 36 S ∆ E Knock-out reactions at β ≈ 0.4 35 P σ (n,L) = C 2 S (j,n,L) σ sp (j,S p ) R S occupancy reaction theory TOF γ 36 S 35 P spectrograph 35 P L=0 S800 L=2 p 9 Be γ E p // 36 S target d 3/2 d 3/2 s 1/2 s 1/2 35 P d 5/2 d 5/2 p 1/2 p 1/2 p 3/2 p 3/2 s 1/2 s 1/2 0 1 u 2 36 S 35 P n,L,j

Probing proton densi6es in 36 S Knock-out reactions at β ≈ 0.4 Gretina array: segmented Ge detectors σ (n,L) = C 2 S(j,n,L) σ sp (j,S p ) R S reaction occupancy theory γ 36 S 35 P p 9 Be E d 3/2 d 3/2 s 1/2 s 1/2 d 5/2 d 5/2 p 1/2 p 1/2 p 3/2 p 3/2 s 1/2 s 1/2 In-flight γ -ray detection-> Doppler corrections 0 1 u 2 36 S 35 P Segmented Ge cristals -> Interaction position

Probing proton densi6es in 36 S Knock-out reactions at β ≈ 0.4 Single γ spectrum σ (n,L) = C 2 S(j,n,L) σ sp (j,S p ) R S 35 P reaction occupancy theory γ 36 S 35 P p 9 Be γ γ coincidences E d 3/2 d 3/2 s 1/2 s 1/2 d 5/2 d 5/2 p 1/2 p 1/2 p 3/2 p 3/2 s 1/2 s 1/2 0 1 u 2 36 S 35 P

Probing proton densi6es in 36 S Energy spectrum Knock-out reactions at β ≈ 0.4 Momentum distrib. L=0 σ (n,L) = C 2 S(j,n,L) σ sp (j,S p ) R S 1.5 L=2 reaction occupancy 15 1.5 2 theory 10 5.5 1 2 3 0.3 2 γ 29 2.7 2 36 S 35 P d σ /d Ω 0.4 2 p 8 9 Be E d 3/2 d 3/2 s 1/2 s 1/2 d 5/2 d 5/2 33 p 1/2 2 0 p 1/2 Σ C 2 S 2 p 3/2 p 3/2 s 1/2 s 1/2 35 P L C 2 S b(%) 0 1 u 2 36 S 35 P Quasi full filling of s 1/2 and d 5/2 orbits (within errors) Only few scattering to the upper d 3/2 orbital. A. Mutschler et al. PRC (2016)

Proton density of 36 S E ρ p (r) 36 S 20 36 S 1d 3/2 0.4 2s 1/2 2 14 1d 5/2 5.5 0 1 u 2 Proton orbits C 2 S(±20%)

Probing proton densi6es in 34 Si Knock-out reactions at β ≈ 0.4 Single γ spectrum σ (n,L) = C 2 S(j,n,L) σ sp (j,S p ) R S reaction occupancy theory γ 34 Si 33 Al p 9 Be γ γ coincidences E d 3/2 d 3/2 s 1/2 s 1/2 d 5/2 d 5/2 p 1/2 p 1/2 p 3/2 p 3/2 s 1/2 s 1/2 0 1 u 2 34 Si 33 Al

Probing proton densi6es in 34 Si Knock-out reactions at β ≈ 0.4 Momentum distrib. Energy spectrum σ (n,L) = C 2 S(j,n,L) σ sp (j,S p ) R S 1.4 0.1 2 L=0 1.4 0.1 0 reaction occupancy L=2 theory 0.2 γ 34 Si 33 Al d σ /d Ω 1.5 0.1 0 0.9 2 14 p 0.2 2 3 9 Be 5.8 E d 3/2 d 3/2 s 1/2 s 1/2 d 5/2 d 5/2 77 p 1/2 4.7 2 p 1/2 p 3/2 p 3/2 s 1/2 s 1/2 33 Al L C 2 S b(%) 0 1 u 2 34 Si 33 Al Very weak 2s 1/2 occupancy -> large central density depletion A. Mutschler et al. to be sumi;ed to Nature

Proton density deple6on in 34 Si E ρ p (r) 36 S 20 36 S 1d 3/2 0.4 2s 1/2 2 14 1d 5/2 5.5 0 1 u 2 Proton orbits C 2 S (±20%) E 34 Si 20 ρ p (r) 34 Si 0 1d 3/2 2s 1/2 0.2 14 ? 1d 5/2 5.8 0 1 u 2 Proton orbits C 2 S (±20%) J.P. Ebran DDME2 interaction Large change in 2s 1/2 occupancy (1.8) -> central proton depletion in 34 Si -> ‘bubble’ nucleus But same neutron density profiles for the two N=20 nuclei

Simplified description of atomic nuclei N=4 ρ (r) g 7/2 2d d 5/2 Spin Orbit 40 1g 50 6, 14, 28, 50, 82, 126 g 9/2 40 r N=3 40 p 1/2 2p U(r) f 5/2 p 3/2 1f r 28 20 f 7/2 20 Harmonic Oscillator 20 8, 20, 40 N=2 d 3/2 2s s 1/2 1d 14 δρ /dr 8 d 5/2 8 r 8 N=1 - δρ /dr L.S U(r) = H.O + L 2 3 3 U ( r ) ( r ' ) v ( r , r ' ) d r ' ( r ' ) [ v ( r r ' )] d r ' v ( r ) = ρ = ρ − ∂ − = − ρ ∫ ∫ 0 0 vol vol