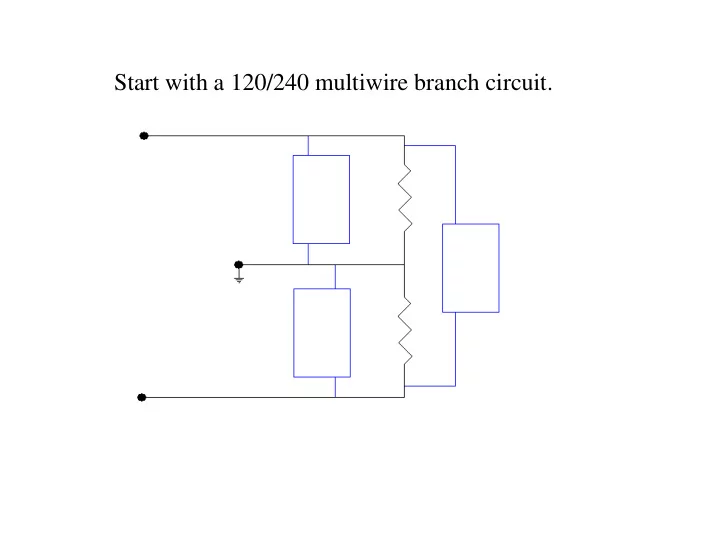
Start with a 120/240 multiwire branch circuit. Well need to begin - PowerPoint PPT Presentation

Start with a 120/240 multiwire branch circuit.

We’ll need to begin with some given values. E= I= R= P= E= I= R= P= E= I= R= P=

We’ll need to begin with some given values. E=120V I= R= P= E=240V I= R= P= E=120V I= R= P=

Now lets add a load to each circuit. E=120V I= R= P= E=240V I= R= P= E=120V I= R= P=

Now lets add a load to each circuit. E=120V I= R= P=100W E=240V I= R= P= E=120V I= R= P=200W

Then calculate amps and resistance for each load. E=120V I= R= P=100W E=240V I= R= P= E=120V I= R= P=200W

Then calculate amps and resistance for each load. E=120V I= R= P=100W E=240V I= R= P= E=120V I= R= P=200W

Then calculate amps and resistance for each load. E=120V I=P/E R= P=100W E=240V I= R= P= E=120V I= R= P=200W

Then calculate amps and resistance for each load. E=120V I=0.8333A R= P=100W E=240V I= R= P= E=120V I= R= P=200W

Then calculate amps and resistance for each load. E=120V I=0.8333A R=E²/P P=100W E=240V I= R= P= E=120V I= R= P=200W

Then calculate amps and resistance for each load. E=120V I=0.8333A R=144 Ω P=100W E=240V I= R= P= E=120V I= R= P=200W

Then calculate amps and resistance for each load. E=120V I=0.8333A R=144 Ω P=100W E=240V I= R= P= E=120V I=P/E R= P=200W

Then calculate amps and resistance for each load. E=120V I=0.8333A R=144 Ω P=100W E=240V I= R= P= E=120V I=1.6667A R= P=200W

Then calculate amps and resistance for each load. E=120V I=0.8333A R=144 Ω P=100W E=240V I= R= P= E=120V I=1.6667A R=E²/P P=200W

Then calculate amps and resistance for each load. E=120V I=0.8333A R=144 Ω P=100W E=240V I= R= P= E=120V I=1.6667A R=72 Ω P=200W

With these values known, we can begin to understand what happens when the neutral is opened. E=120V I=0.8333A R=144 Ω P=100W E=240V I= R= P= E=120V I=1.6667A R=72 Ω P=200W

First, we’ll open the neutral conductor. E=120V I=0.8333A R=144 Ω P=100W E=240V I= R= P= E=120V I=1.6667A R=72 Ω P=200W

First, we’ll open the neutral conductor. E=120V I=0.8333A R=144 Ω P=100W E=240V I= R= P= E=120V I=1.6667A R=72 Ω P=200W

In doing so, we no longer have two circuits, but only one. The two loads are now in series. E=120V I=0.8333A R=144 Ω P=100W E=240V I= R= P= E=120V I=1.6667A R=72 Ω P=200W

So we will erase the figures we have calculated so far. E=120V I=0.8333A R=144 Ω P=100W E=240V I= R= P= E=120V I=1.6667A R=72 Ω P=200W

So we will erase the figures we have calculated so far. E= I=0.8333A R=144 Ω P=100W E=240V I= R= P= E=120V I=1.6667A R=72 Ω P=200W

So we will erase the figures we have calculated so far. E= I= R=144 Ω P=100W E=240V I= R= P= E=120V I=1.6667A R=72 Ω P=200W

So we will erase the figures we have calculated so far. Leave the values of R in place. Those will not change. E= I= R=144 Ω P= E=240W I= R= P= E=120V I=1.6667A R=72 Ω P=200W

So we will erase the figures we have calculated so far. Leave the values of R in place. Those will not change. E= I= R=144 Ω P= E=240V I= R= P= E= I=1.6667A R=72 Ω P=200W

So we will erase the figures we have calculated so far. Leave the values of R in place. Those will not change. E= I= R=144 Ω P= E=240V I= R= P= E= I= R=72 Ω P=200W

So we will erase the figures we have calculated so far. Leave the values of R in place. Those will not change. E= I= R=144 Ω P= E=240V I= R= P= E= I= R=72 Ω P=

Now add the values of the two loads’ resistances. E= I= R=144 Ω P= E=240V I= R= P= E= I= R=72 Ω P=

Now add the values of the two loads’ resistances. E= I= R=144 Ω P= E=240V I= R=144+72 P= E= I= R=72 Ω P=

Now add the values of the two loads’ resistances. E= I= R=144 Ω P= E=240V I= R=216 Ω P= E= I= R=72 Ω P=

Now calculate I and P for the entire circuit. E= I= R=144 Ω P= E=240V I= R=216 Ω P= E= I= R=72 Ω P=

Now calculate I and P for the entire circuit. E= I= R=144 Ω P= E=240V I=E/R R=216 Ω P= E= I= R=72 Ω P=

Now calculate I and P for the entire circuit. E= I= R=144 Ω P= E=240V I=1.1111A R=216 Ω P= E= I= R=72 Ω P=

Now calculate I and P for the entire circuit. E= I= R=144 Ω P= E=240V I=1.1111A R=216 Ω P=E²/R E= I= R=72 Ω P=

Now calculate I and P for the entire circuit. E= I= R=144 Ω P= E=240V I=1.1111A R=216 Ω P=266.7W E= I= R=72 Ω P=

Since this is a series circuit, I is always the same. E= I= R=144 Ω P= E=240V I=1.1111A R=216 Ω P=266.7W E= I= R=72 Ω P=

Since this is a series circuit, I is always the same. E= I=1.1111A R=144 Ω P= E=240V I=1.1111A R=216 Ω P=266.7W E= I= R=72 Ω P=

Since this is a series circuit, I is always the same. E= I=1.1111A R=144 Ω P= E=240V I=1.1111A R=216 Ω P=266.7W E= I=1.1111A R=72 Ω P=

Now calculate the voltage across each of the two loads. E= I=1.1111A R=144 Ω P= E=240V I=1.1111A R=216 Ω P=266.7W E= I=1.1111A R=72 Ω P=

Now calculate the voltage across each of the two loads. E=R*I I=1.1111A R=144 Ω P= E=240V I=1.1111A R=216 Ω P=266.7W E= I=1.1111A R=72 Ω P=

Now calculate the voltage across each of the two loads. E=160V I=1.1111A R=144 Ω P= E=240V I=1.1111A R=216 Ω P=266.7W E= I=1.1111A R=72 Ω P=

Now calculate the voltage across each of the two loads. E=160V I=1.1111A R=144 Ω P= E=240V I=1.1111A R=216 Ω P=266.7W E=R*I I=1.1111A R=72 Ω P=

Now calculate the voltage across each of the two loads. E=160V I=1.1111A R=144 Ω P= E=240V I=1.1111A R=216 Ω P=266.7W E=80V I=1.1111A R=72 Ω P=

Now you can see what happens when you lose the neutral on a multiwire branch circuit. E=160V I=1.1111A R=144 Ω P= E=240V I=1.1111A R=216 Ω P=266.7W E=80V I=1.1111A R=72 Ω P=

The more resistance, the higher the voltage.... E= 160V I=1.1111A R= 144 Ω P= E=240V I=1.1111A R=216 Ω P=266.7W E=80V I=1.1111A R=72 Ω P=

The less resistance, the lower the voltage. E=160V I=1.1111A R=144 Ω P= E=240V I=1.1111A R=216 Ω P=266.7W E= 80V I=1.1111A R= 72 Ω P=

This is Ohm’s Law in a most practical use, and the reason Article 300.13(B) exists. E=160V I=1.1111A R=144 Ω P= E=240V I=1.1111A R=216 Ω P=266.7W E=80V I=1.1111A R=72 Ω P=