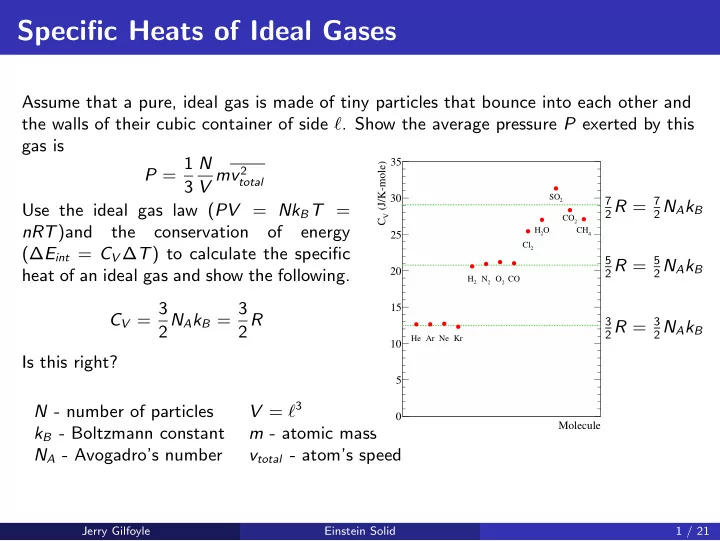
Specific Heats of Ideal Gases Assume that a pure, ideal gas is made - PowerPoint PPT Presentation

Specific Heats of Ideal Gases Assume that a pure, ideal gas is made of tiny particles that bounce into each other and the walls of their cubic container of side ℓ . Show the average pressure P exerted by this gas is P = 1 N 35 (J/K-mole) V mv 2 total 3 30 SO 7 2 R = 7 2 2 N A k B Use the ideal gas law ( PV = Nk B T = V CO C 2 nRT )and the conservation of energy H O CH 25 2 4 Cl (∆ E int = C V ∆ T ) to calculate the specific 2 2 R = 5 5 2 N A k B heat of an ideal gas and show the following. 20 H N O CO 2 2 2 C V = 3 2 N A k B = 3 15 2 R 3 2 R = 3 2 N A k B He Ar Ne Kr 10 Is this right? 5 V = ℓ 3 N - number of particles 0 Molecule k B - Boltzmann constant m - atomic mass N A - Avogadro’s number v total - atom’s speed Jerry Gilfoyle Einstein Solid 1 / 21

A Hint of Quantum Mechanics H 2 gas Jerry Gilfoyle Einstein Solid 2 / 21

Rotational Kinetic Energy Classically E rot = L 2 2 I where � � mr 2 r 2 dm I = i = Jerry Gilfoyle Einstein Solid 3 / 21

Rotational Kinetic Energy Classically E rot = L 2 2 I where � � mr 2 r 2 dm I = i = Quantum mechanically rot = ℓ ( ℓ + 1) � 2 E qm 2 I where l is the angular momen- tum quantum number. Jerry Gilfoyle Einstein Solid 3 / 21

The Specific Heat of Elemental Solids - 1 R = 8 . 31 J / mol K Jerry Gilfoyle Einstein Solid 4 / 21

The Specific Heat of Elemental Solids - 2 Solid Molar Specific Heat Our Results (J/K-mole) (J/K-mole) Lead 26 . 4 22 ± 6 Zinc 25 . 4 36 ± 14 Aluminum 26 . 4 24 ± 5 Copper 24 . 5 23 ± 5 Tin 27 . 0 52 ± 15 Gold 25 . 4 Silver 25 . 4 Iron 25 . 0 Jerry Gilfoyle Einstein Solid 5 / 21

The Einstein Solid Cell boundaries atoms Jerry Gilfoyle Einstein Solid 6 / 21

Molar Specific Heat of Elemental Solids An Einstein solid is made of N , three-dimensional harmonic oscillators containing q quanta of energy. 1 What is the multiplicity of Molar Specific Solid Heat Our Results a single Einstein solid? (J/K-mole) (J/K-mole) Lead 26 . 4 ± 0 . 7 22 ± 6 2 What is the multiplicity of Zinc 25 . 4 ± 0 . 6 36 ± 14 two Einstein solids in ther- Aluminum 26 . 4 ± 0 . 2 24 ± 3 mal contact? Copper 24 . 5 ± 0 . 6 23 ± 5 3 How would you determine Tin 27 . 0 ± 0 . 6 52 ± 15 Gold 25 . 4 ± 0 . 6 the most likely microstate Silver 25 . 4 ± 0 . 6 of the system? Iron 25 . 0 ± 0 . 6 4 How is entropy related to temperature? 5 How is the energy related to temperature? 6 What is the molar specific heat of an elemental solid? Jerry Gilfoyle Einstein Solid 7 / 21

Rolling Dice Jerry Gilfoyle Einstein Solid 8 / 21

A Probability Distribution Throwing Dice Number of Events 6 5 4 3 2 1 0 0 2 4 6 8 10 12 14 16 Sum Jerry Gilfoyle Einstein Solid 9 / 21 2014-12-30 19:21:22

The Entropy of the Einstein Solid An Einstein solid is made of N , three-dimensional harmonic oscillators containing q quanta of energy as shown below. 1 What is the energy of a single oscillator? of N oscillators? 2 How many microstates Ω exist for a ‘system’ with N = 1 and q = 3? for N = 2, q = 2? 3 What is Ω for any N and q ? Jerry Gilfoyle Einstein Solid 10 / 21

Microstates for N A = 2 , q A = 2 n 1 n 2 n 3 n 4 n 5 n 6 n 1 n 2 n 3 n 4 n 5 n 6 Jerry Gilfoyle Einstein Solid 11 / 21

Microstates for N A = 2 , q A = 2 Jerry Gilfoyle Einstein Solid 12 / 21

Summary So Far 3 N � E int = ( n x + n y + n z ) � ω = n i � ω for N atoms i =1 multiplicity (Ω) number of microstates macrostate configuration of a solid defined by bulk proper- ties like N and E / U . microstate one of the configurations of quanta consistent with the macrostate. Ω( N A , q A ) = ( q A + 3 N A − 1)! q A !(3 N A − 1)! Ω AB - multiplicity of combined state Ω AB = Ω A Ω B where Ω A , B - individual multiplicities. Jerry Gilfoyle Einstein Solid 13 / 21

Multiplicity and Number of Quanta Einstein Solid 2.0 red � B black � A � B blue � A x10 � 54 1.5 N A � 30 N B � 25 q AB � 200 � 1.0 x10 � 32 0.5 x10 � 37 0.0 0 50 100 150 200 q a Jerry Gilfoyle Einstein Solid 14 / 21

Some Math - Logarithms Jerry Gilfoyle Einstein Solid 15 / 21

Entropy of Two Einstein Solids S AB Entropy S B Equilibrium Point S A q a Jerry Gilfoyle Einstein Solid 16 / 21

Entropy of Two Einstein Solids in Energy Terms S AB Entropy S B Equilibrium Point S A E a Jerry Gilfoyle Einstein Solid 17 / 21

The Specific Heat of Elemental Solids Measured Our Solid Molar Specific Heat Our Results Calculation (J/K-mole) (J/K-mole) (J/K-mole) Lead 26 . 4 ± 0 . 7 22 ± 8 24 . 9 Zinc 25 . 4 ± 0 . 6 36 ± 14 24 . 9 Aluminum 26 . 4 ± 0 . 2 24 ± 3 24 . 9 Copper 24 . 5 ± 0 . 6 23 ± 5 24 . 9 Tin 27 . 0 ± 0 . 6 52 ± 15 24 . 9 Gold 25 . 4 ± 0 . 6 24 . 9 Silver 25 . 4 ± 0 . 6 24 . 9 Iron 25 . 0 ± 0 . 6 24 . 9 Jerry Gilfoyle Einstein Solid 18 / 21

The Harmonic Oscillator Approximation Harmonic Oscillator Potential � red � Potential Energy True Potential � green � Displacement From Equilibrium Jerry Gilfoyle Einstein Solid 19 / 21

Quantum Oscillator Jerry Gilfoyle Einstein Solid 20 / 21

Updating equilib.exe Go to: h ttp://www.physics.pomona.edu/sixideas/sicpr.html 1 Scroll down to the section entitled “For Use With Unit T:”. 2 Scroll down to the paragraph that starts with “Equilib 2.1”. 3 Scroll down to “Download for:” and right click on “Windows” and save it to your 4 Desktop. Double click on the folder entitled “Equil.exe.zip”. You should see a list of the 5 contents of the folder. Double click on “ Equilib.exe ”. You should get a GUI telling you the application 6 may depend on other compressed files in the folder. Click the “ Extract All ” button and then choose the Desktop to place the files. Double click on “ Equilib.exe ” and you will now see the contents of the folder with 7 the application. Double click on “ Equilib.exe ”. You will get a GUI worrying about the publisher. 8 Click “ Run ” and you’re off. 9 Jerry Gilfoyle Einstein Solid 21 / 21