Spanning Trees Recall the definitions of: - graphs, the vertex set - PowerPoint PPT Presentation

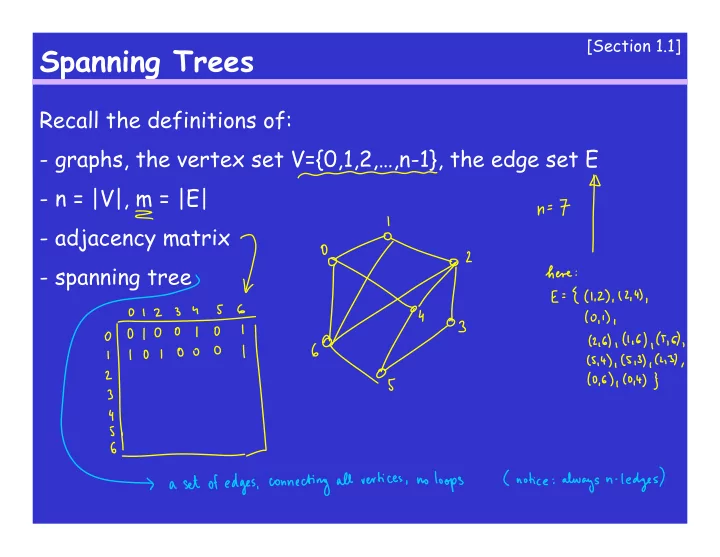
[Section 1.1] Spanning Trees Recall the definitions of: - graphs, the vertex set V={0,1,2,…,n-1}, the edge set E - n = |V|, m = |E| - adjacency matrix - spanning tree

[Section 1.1] Spanning Trees Thm 1.1 (Kirchhoff): Let A be the adjacency matrix of an undirected graph and D be the diagonal matrix with the degrees of vertices on its diagonal. Then, for every i ∈ {0,1,2,…,n-1}: # spanning trees of G = det (D-A) ii Where (D-A) ii is an (n-1)x(n-1) submatrix obtained from D-A by removing the i-th row and the i-th column.

[Section 1.1] Spanning Trees Thm (Kirchhoff): Let A be the adjacency matrix of an undirected graph and D be the diagonal matrix with the degrees of vertices on its diagonal. Then, for every i ∈ {0,1,2,…,n-1}: # spanning trees of G = det (D-A) ii Where (D-A) ii is an (n-1)x(n-1) submatrix obtained from D-A by removing the i-th row and the i-th column. Note: determinant can be computed in time O(n 3 )

[Section 1.1] Spanning Trees Lemma (Binet-Cauchy): If A is an (rxm) matrix and B is an (mxr) matrix, then: det(A.B) = ∑ S ⊆ [m], |S|=r det(A *S ).det(B S* ) Where A *S is the (rxr) matrix obtained from A by keeping only the columns in S, and B S* is the (rxr) matrix obtained from B by keeping only the rows in S.

[Section 1.1] Spanning Trees Def: Incidence matrix of a directed graph H: an (nxm) matrix N=( ν ve ) such that: +1 if e starts at v ν ve = -1 if e ends at v 0 o\w

[Section 1.1] Spanning Trees Fact 1.6: rank N = n - # weakly connected components of H

[Section 1.1] Spanning Trees Fact 1.6: rank N = n - # weakly connected components of H

[Section 1.1] Spanning Trees Fact 1.7: If B is a square matrix with entries in {+1,-1,0} and every column has at most one +1 and at most one -1. Then, det(B) is +1, -1, or 0.

[Section 1.1] Spanning Trees Thm 1.1 (Kirchhoff): # spanning trees = det (D-A) ii Proof:

[Section 1.1] Spanning Trees Thm 1.1 (Kirchhoff): # spanning trees = det (D-A) ii Proof: