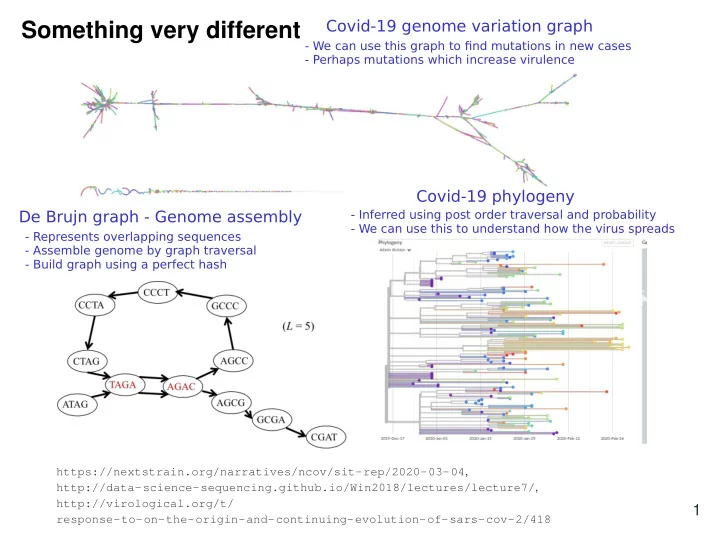

Covid-19 genome variation graph Something very different - We can use this graph to fi nd mutations in new cases - Perhaps mutations which increase virulence Covid-19 phylogeny De Brujn graph - Genome assembly - Inferred using post order traversal and probability - We can use this to understand how the virus spreads - Represents overlapping sequences - Assemble genome by graph traversal - Build graph using a perfect hash https://nextstrain.org/narratives/ncov/sit-rep/2020-03-04 , http://data-science-sequencing.github.io/Win2018/lectures/lecture7/ , http://virological.org/t/ 1 response-to-on-the-origin-and-continuing-evolution-of-sars-cov-2/418
Back to hashing Ignoring this for now but p should be bigger than m so we map to all parts of the hash table (( ax + b ) mod p ) mod m 8 0 Warmup: Find the largest set of keys that collide 7 1 2 6 hash ( x ) = ( 3 x + 2 ) mod9 3 5 4 Any value of the form 3i where i is an integer collides This is bad as we could only map to part of the hash table 10 0 1 9 2 hash ( x ) = ( 3 x + 2 ) mod11 8 3 7 Any value of the form 11i collides 6 4 5 This is better because we map to all values from 0 - 10 Which is a better hash function? The second function is better because 3 is relatively prime to 11 which results in fewer collisions because it avoids degeneracy, that is getting trapped in cycles that don't map to all the possible values. 2
Hashing with chaining hash(AT)=hash(GA)=1 Store multiple key in each array slot Keys We can store lots of keys but performance degrades 0 How? 1 AT GA • We will consider linked lists • Any dictionary ADT could be 2 must consider if keys used provided ... 3 are comparable (ordered) Result (using linked list) 4 CT • We can hash more than m things 5 into an array of size m 6 AA TA • Worst case runtime depends on d["A"] = 1 length of largest chain d["A"] = 2 print d["A"] ? • Memory is allocated on each We could insert at head or tail of linked insert list since we need to check if key exists This could lead to bad memory/cache so we must traverse anyways 3 performance
Acces time for chaining Why do we need this to think about runtime? Load factor: # items hashed # size of array = n = α m Assuming a uniform hash function i.e. probability of hashing to any slot is equal Hash to a location with an average of α items Search cost: • Unsuccessful search examines items α • Successful search examines 1 + n − 1 2 m = 1 + α 2 − α 2 n items Pay for fi rst item Average # remaining items For good performance we want a small load factor Our query key is on average 1/2 way through 4
hash(AT)=hash(GA)=hash(GT)=1 Open adressing GT Clustering Each array element contains one item. The hash 0 TA function speci fi es a sequence of elements to try. Insert: If fi rst slot is occupied check next location in 1 AT hash function sequence. Find: If slot does not match keep trying the next slot in 2 GA sequence until either the item is found or an empty slot is visited (item not found). 3 GT Remove: Find and replace item with a tombstone . 4 CT remove(AA) Result: • Cannot hash more than m items by pigeonhole 5 principle • Hash table memory allocated once 6 AA • Performance will depend on how many times we check slots Wrap around using mod m 5
Linear probing Try ( h ( k ) + i ) mod m for i = 0 , 1 , 2 ,... m − 1 insert(83) insert(76) insert(14) insert(42) 0 14 14 14 1 42 42 2 83 3 4 5 6 76 76 76 76 For this example h ( k ) = k mod7 and m = 7 6
Double hashing Try ( h ( k ) + i · h 2 ( k )) mod m for i = 0 , 1 , 2 ,... m − 1 insert(76) insert(14) insert(42) insert(83) 0 14 14 14 1 83 2 3 42 42 4 5 6 76 76 76 76 For this example h ( k ) = k mod7, h 2 ( k ) = 5 − k mod 5 and m = 7 Does not hash to 0! 7
Rehashing Sometimes we need to resize the hash table • For open addressing this will have to happen when we fi ll the table • For separate chaining we want to do this when the load factor gets big To resize we: • Resize the hash table • Θ ( 1 ) amortized time if doubling One reason we need a new value for mod m • Get a new hash function since the table size changes Result: Because we have a new hash function • Spread the keys out • Remove tombstones (open addressing) • Allows arbitrarily large tables 8
Hashing summary What collision resolution strategy is best? High load factor: Chaining is better, open addressing su ff ers from clustering Open addressing can have better memory performance, fewer memory allocations What is the best implementation of a dictionary ADT? AVL Hash table Worst case: Θ (log 2 ( n )) Θ ( n ) Lots of collisions Θ (1) Average case: Θ (log 2 ( n )) Why did we talk about trees? AVL trees can make use of the fact keys are comparable for fast operations: Find the max - Keep going right Θ (log 2 ( n )) Range queries - Find all values less than a key More in depth info: http://jeffe.cs.illinois.edu/teaching/ algorithms/notes/05-hashing.pdf 9
Is this a BST? Something new No. Does not have search property. What is interesting about this tree? 1. It is complete - All layers full except last where all nodes are as far left as 2 possible 2. Every node is greater than its children. Implies root is min. 5 6 9 8 7 14 29 21 42 15 33 Where should we insert next? 10
Recommend
More recommend