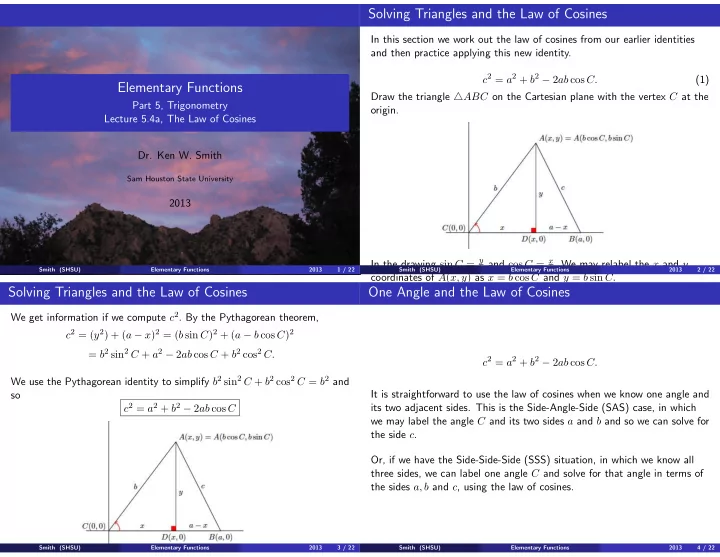
Solving Triangles and the Law of Cosines In this section we work out - PowerPoint PPT Presentation

Solving Triangles and the Law of Cosines In this section we work out the law of cosines from our earlier identities and then practice applying this new identity. c 2 = a 2 + b 2 − 2 ab cos C. (1) Elementary Functions Draw the triangle △ ABC on the Cartesian plane with the vertex C at the Part 5, Trigonometry origin. Lecture 5.4a, The Law of Cosines Dr. Ken W. Smith Sam Houston State University 2013 In the drawing sin C = y b and cos C = x b . We may relabel the x and y Smith (SHSU) Elementary Functions 2013 1 / 22 Smith (SHSU) Elementary Functions 2013 2 / 22 coordinates of A ( x, y ) as x = b cos C and y = b sin C. Solving Triangles and the Law of Cosines One Angle and the Law of Cosines We get information if we compute c 2 . By the Pythagorean theorem, c 2 = ( y 2 ) + ( a − x ) 2 = ( b sin C ) 2 + ( a − b cos C ) 2 = b 2 sin 2 C + a 2 − 2 ab cos C + b 2 cos 2 C. c 2 = a 2 + b 2 − 2 ab cos C. We use the Pythagorean identity to simplify b 2 sin 2 C + b 2 cos 2 C = b 2 and It is straightforward to use the law of cosines when we know one angle and so c 2 = a 2 + b 2 − 2 ab cos C its two adjacent sides. This is the Side-Angle-Side (SAS) case, in which we may label the angle C and its two sides a and b and so we can solve for the side c . Or, if we have the Side-Side-Side (SSS) situation, in which we know all three sides, we can label one angle C and solve for that angle in terms of the sides a, b and c , using the law of cosines. Smith (SHSU) Elementary Functions 2013 3 / 22 Smith (SHSU) Elementary Functions 2013 4 / 22

A Worked Problem. A Worked Problem. Solve the triangle C = 32 ◦ , a = 100 feet , b = 150 feet . Solution. If C = 32 ◦ , a = 100 feet , b = 150 feet then, by the law of We solve the triangle C = 32 ◦ , a = 100 feet , b = 150 feet . cosines ( c 2 = a 2 + b 2 − 2 ab cos C ), We found c 2 = (100) 2 + (150) 2 − 2(100)(150) cos(32 ◦ ) ≈ 7059 . A ≈ sin − 1 (0 . 63007) ≈ 39 . 1 ◦ or A ≈ 180 − 39 . 1 = 140 . 9 ◦ . So √ c ≈ 7059 ≈ 84 . 018 feet. The second answer is too big, so A = 39 . 1 ◦ . Now we apply the law of sines: Since sin B = 0 . 9461 then either sin 32 ◦ 84 . 018 = sin A 100 = sin B 150 B ≈ sin − 1 (0 . 94510) ≈ 71 . 1 ◦ or B = 180 − 71 . 1 = 108 . 9 ◦ . This forces sin A = 100 sin 32 ◦ The second answer, B = 108 . 9 ◦ , makes perfect sense because the angles ≈ 0 . 6307 84 . 018 of the triangle need to add up to 180 degrees. and sin B = 150 sin 32 ◦ ≈ 0 . 9461 84 . 018 If the sine of A is 0 . 6307 then either A ≈ sin − 1 (0 . 63007) ≈ 39 . 1 ◦ or A ≈ 180 − 39 . 1 = 140 . 9 ◦ . Smith (SHSU) Elementary Functions 2013 5 / 22 Smith (SHSU) Elementary Functions 2013 6 / 22 The law of cosines and SSS The law of cosines and SSS Solve the triangle a = 30 feet , b = 20 feet , c = 15 feet . We solve the triangle a = 30 feet , b = 20 feet , c = 15 feet . Solution. If a = 30 feet , b = 20 feet , c = 15 feet then the law of cosines We found A = 62 . 7 ◦ or A = 180 ◦ − 62 . 7 ◦ = 117 . 3 ◦ tells us that 15 2 − 30 2 − 20 2 = cos C Also − 2(30)(20) sin B = 4 so 3 sin 26 . 38 ◦ − 1075 − 1200 = 43 48 = cos C so B = 36 . 33 ◦ or 180 ◦ − 36 . 33 ◦ = 143 . 67 ◦ Therefore C = cos − 1 (43 48) ≈ 26 . 38 ◦ . The second result here is too large. By the law of sines Our final answer, after checking that angles add up to 180 ◦ , is sin 26 . 38 ◦ = sin A = sin B 20 , 15 30 A = 117 . 3 ◦ , B = 36 . 3 ◦ , C = 26 . 4 ◦ . so sin A = 2 sin 26 . 38 ◦ . and so A = 62 . 7 ◦ or A = 180 ◦ − 62 . 7 ◦ = 117 . 3 ◦ Smith (SHSU) Elementary Functions 2013 7 / 22 Smith (SHSU) Elementary Functions 2013 8 / 22

Some Worked Problems. Some Worked Problems. A triangle has angle C = 20 ◦ and sides a = 10 , b = 20 . Use the law of cosines to find the length of the side c . A triangle has angle C = 20 ◦ and sides a = 10 , b = 20 . Use the law of sines to find two possible values of the angle B (one in which B is acute Solution. and one in which B is obtuse.) c 2 = 10 2 + 20 2 − 2(10)(20) cos 20 ◦ = 500 − 400 cos 20 ◦ ≈ 124 . 1 Solution. The sine of B is 0 . 614 so B ≈ 37 . 88 ◦ or 142 . 12 ◦ . √ So c ≈ 124 . 1 ≈ 11 . 14 . Solve the triangle. Solution. c ≈ 11 . 14 , A ≈ 17 . 88 ◦ and B ≈ 142 . 12 ◦ . Use the law of sines to find two possible values of the angle A (one in which A is acute and one in which A is obtuse.) Solution. The sine of A is 0 . 307 so A = 17 . 88 ◦ or 162 . 12 ◦ . Smith (SHSU) Elementary Functions 2013 9 / 22 Smith (SHSU) Elementary Functions 2013 10 / 22 Solving Triangles and the Law of Cosines Solving Triangles and the Law of Cosines Solve the triangles with sides a = 15 , b = 12 , c = 30 . Solve the triangle with sides a = 15 , b = 12 , c = 10 . Solution. Since one side is longer than the sum of the other two sides, Solution. By the Law of Cosines, C = 41 . 65 ◦ . Now use the Law of Sines no such triangle is possible. to get (No calculations are necessary here. If we did a calculation, we would a = 15 , b = 12 , c = 10 , A = 85 . 46 ◦ , B = 52 . 89 ◦ , C = 41 . 65 ◦ . eventually take the arccosine of a number larger than 1, which is impossible.) Smith (SHSU) Elementary Functions 2013 11 / 22 Smith (SHSU) Elementary Functions 2013 12 / 22

The Law of Cosines Elementary Functions Part 5, Trigonometry In the next presentation, we will look at Heron’s formula and the “Five Lecture 5.4b, Heron’s Formula, Five Guys Guys”, (five trig identities I give to my classes.) Dr. Ken W. Smith (End) Sam Houston State University 2013 Smith (SHSU) Elementary Functions 2013 13 / 22 Smith (SHSU) Elementary Functions 2013 14 / 22 The area of an oblique triangle The area of an oblique triangle Since a triangle is half of a parallelogram, its area is one-half of the K = 1 product of its base and height. 2 ab sin C (3) Let K represent the area of a triangle. Looking at the drawing below, we see that We can summarize this by saying that the area of a triangle is one-half of K = 1 2 ch. the product of the sine of an angle and its neighboring sides. But earlier, in our proof of the Law of Sines, we solved for h and we wrote h = b sin A and h = a sin B. So we can substitute for h and write the area as K = 1 2 cb sin A and K = 1 2 ac sin B Or we could call the known angle C and just write K = 1 2 ab sin C (2) Smith (SHSU) Elementary Functions 2013 15 / 22 Smith (SHSU) Elementary Functions 2013 16 / 22

Heron’s formula Heron’s formula Let’s take the area equation K = 1 2 ab sin C and square both sides. If we know the three sides a, b and c then in theory, since the triangle is K 2 = 1 4 a 2 b 2 sin 2 C. fixed and we can compute the three angles, we should be able to compute By the Pythagorean identity replace sin 2 C by 1 − cos 2 C the area of the triangle. A first step is the formula we found when we proved the Law of Sines: K 2 = 1 4 a 2 b 2 (1 − cos 2 C ) . K = 1 and distribute 2 ab sin C K 2 = 1 4 a 2 b 2 cos 2 C. 4 a 2 b 2 − 1 A succinct formula for the area of a triangle, given the three sides, was Now use the Law of Cosines in the form worked out long ago by Heron of Alexandria. cos C = a 2 + b 2 − c 2 2 ab to replace cos 2 C : K 2 = 1 4 a 2 b 2 − ( 1 4 a 2 b 2 )( a 2 + b 2 − c 2 ) 2 2 ab and simplify K 2 = 1 16 )( a 2 + b 2 − c 2 ) 2 4 a 2 b 2 − ( 1 Smith (SHSU) Elementary Functions 2013 17 / 22 Smith (SHSU) Elementary Functions 2013 18 / 22 Heron’s formula Summary & Five Guys Using the law of sine and the law of cosines, we worked out a formula for the area: Summary of our identities K 2 = 1 16 )( a 2 + b 2 − c 2 ) 2 4 a 2 b 2 − ( 1 We have come across two very useful identities that are easy to remember: K 2 = 1 16 (4 a 2 b 2 − ( a 2 + b 2 − c 2 ) 2 ) 1 The Pythagorean identity, cos 2 θ + sin 2 θ = 1 (and its two siblings), Now, with a little bit of algebra ... (skipping a bunch of steps!) ... we can get this into the form and K 2 = ( a + b + c 2 The Law of Sines, sin A = sin B = sin C )( − a + b + c )( a − b + c )( a + b − c ) c . a b 2 2 2 2 The perimeter of the triangle is a + b + c. Half of the perimeter, written There are five more identities that are very useful and if we know them (or s = a + b + c is called the semiperimeter. have them handy) then the other trig identities follow easily from them. 2 We can use the semiperimeter s to shorten this equation Our goal here is understanding, not memorization! But if one were to K 2 = s ( s − a )( s − b )( s − c ) . memorize trig identities, in addition to the easy two above, I recommend the following five. So the area of a triangle is � K = s ( s − a )( s − b )( s − c ) . This is Heron’s formula Smith (SHSU) Elementary Functions 2013 19 / 22 Smith (SHSU) Elementary Functions 2013 20 / 22

Five Guys Five Guys 1 The formulas for the sine and cosine of the sum of two angles: cos( α + β ) = cos α cos β − sin α sin β sin( α + β ) = sin α cos β + cos α sin β 2 The power reduction formulas: cos 2 α = 1+cos(2 α ) In the next presentation, we will look at polar coordinates. 2 sin 2 α = 1 − cos(2 α ) 2 (End) c 2 = a 2 + b 2 − 2 ab cos C 3 The law of cosines: In my precalculus and trigonometry classes these five identities, boxed above, will be provided on quizzes and exams. Since I have never memorized these – and I’ve done well in mathematics, emphasizing understanding over memorization – then I won’t ask my students to memorize them. Students should focus on understanding how to wield these five guys in a variety of environments. Smith (SHSU) Elementary Functions 2013 21 / 22 Smith (SHSU) Elementary Functions 2013 22 / 22