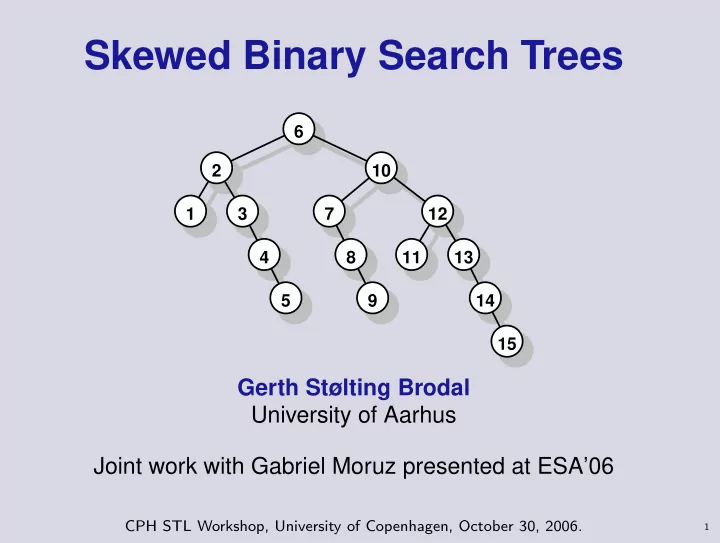
Skewed Binary Search Trees 6 2 10 1 3 7 12 4 8 11 13 5 9 - PowerPoint PPT Presentation

Skewed Binary Search Trees 6 2 10 1 3 7 12 4 8 11 13 5 9 14 15 Gerth Stølting Brodal University of Aarhus Joint work with Gabriel Moruz presented at ESA’06 CPH STL Workshop, University of Copenhagen, October 30, 2006. 1

Perfectly Balanced Search Trees 8 4 12 2 6 10 14 1 3 5 7 9 11 13 15 Skewed Binary Search Trees 2

Skewed Binary Search Trees x α ⌊ α ( n − 1) ⌋ 1 − α ⌈ (1 − α )( n − 1) ⌉ Skewed Binary Search Trees 3

Skewed Binary Search Trees 8 4 12 2 6 10 14 1 3 5 7 9 11 13 15 α = 0 . 5 Skewed Binary Search Trees 4

Skewed Binary Search Trees 6 2 10 1 3 7 12 4 8 11 13 5 9 14 15 α = 0 . 4 Skewed Binary Search Trees 5

Skewed Binary Search Trees 3 1 6 2 4 8 5 7 10 9 11 12 α = 0 . 2 13 14 15 Skewed Binary Search Trees 6

Skewed Binary Search Trees 1 2 3 4 5 6 7 8 9 10 11 12 α = 0 . 05 13 14 15 Skewed Binary Search Trees 7

Skewed Binary Search Trees — Average Node Depth 1 · n + 1 ≤ · log 2 ( n + 1) − 2 − α log 2 α − (1 − α ) log 2 (1 − α ) n � �� � H ( α ) Nievergelt and E. M. Reingold, 1972 Skewed Binary Search Trees 8

1 /H ( α ) 10 8 6 1 /H ( α ) 4 2 0 0 0.2 0.4 0.6 0.8 1 α Skewed Binary Search Trees 9

Comparisons 3.5e+08 3e+08 2.5e+08 Comparisons 2e+08 1.5e+08 1e+08 5e+07 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 α n = 50 . 000 Skewed Binary Search Trees 10

Running Time 0.28 0.275 0.27 Running time 0.265 0.26 0.255 0.25 0.245 0.24 0.235 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 α Best running time achieved for α ≈ 0 . 3 !? Skewed Binary Search Trees 11

Conclusion Skewed binary search trees can beat Perfectly balanced binary search trees ! Skewed Binary Search Trees 12

Why ? Skewed Binary Search Trees 13

Why ? The costs going left and right are different ! Possible reasons • Number of instructions • Branch mispredictions • Cache faults (what is a good memory layout?) • ... Skewed Binary Search Trees 14

Expected Cost cost ( α ) = ( α · {left cost} + (1 − α ) · {right cost} ) /H ( α ) 8 7 6 5 cost ( α ) 4 3 2 1 0 0 0.2 0.4 0.6 0.8 1 α left cost = 1 and right cost = 3 Skewed Binary Search Trees 15

Expected Cost cost ( α ) = ( α · {left cost} + (1 − α ) · {right cost} ) /H ( α ) 8 7 6 5 cost ( α ) 4 3 2 1 0 0 0.2 0.4 0.6 0.8 1 α left cost = 1 and right cost = 0 .. 28 Skewed Binary Search Trees 16

Experimental setup • AMD Athlon XP 2400+ • 2.0 GHz • 256 KB L2 cache • 64 KB L1 data cache • 64 KB L1 instruction cache • 1GB RAM • Linux 2.6.8.1 • GCC 3.3.2 • Tree nodes = 12 bytes • No unsuccesful searches Skewed Binary Search Trees 17

Search Code while(root!=NULLV) { if(key==t[root].key) return root; if(key>t[root].key) root=t[root].right; else root=t[root].left; } Skewed Binary Search Trees 18

Branch Mispredictions 8e+06 7e+06 Branch mispredictions 6e+06 5e+06 4e+06 3e+06 2e+06 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 α n = 50 . 000 Skewed Binary Search Trees 19

Simple Layouts 4 5 1 7 6 2 3 Random – O ( log n H ( α ) ) I/Os 3 1 2 3 4 5 6 7 Inorder – O ( log n H ( α ) − log B ) I/Os 1 5 2 4 6 3 1 5 2 4 6 7 BFS – O ( log n H ( α ) − log B ) I/Os 7 3 5 6 7 4 1 2 DFSr – O ( α +(1 − α ) /B · log n ) I/Os. H ( α ) Skewed Binary Search Trees 20

Running Time for Simple Layouts 0.4 DFSl DFSr 0.35 BFS Inord Rand Running time 0.3 0.25 0.2 0.15 0.1 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 α DFS < Inorder < BFS < Random DFS achieves the best performance for α ≈ 0 . 2 ! Skewed Binary Search Trees 21

Cache Faults for Simple Layouts 3e+07 DFSl DFSr 2.5e+07 BFS Inord Rand Cache misses 2e+07 1.5e+07 1e+07 5e+06 0 0 0.2 0.4 0.6 0.8 1 α DFS ≈ expected left cost = 1 and right cost = 1 /B . Skewed Binary Search Trees 22

Blocked Layouts — k -level blocking 6 2 10 1 3 7 12 4 8 11 13 5 9 14 k = 2 15 6 2 10 1 3 4 5 7 8 9 12 11 13 14 15 • layout the nodes of the first k levels • recurse on subtrees • a search uses O (log B n/H ( α )) I/Os Skewed Binary Search Trees 23

Blocked Layouts — pqDFS k 15 6 5 9 2 10 3 1 5 1 3 7 12 3 3 2 2 1 4 8 11 13 2 1 1 5 9 14 k = 3 15 1 6 10 2 12 13 14 15 11 7 8 9 3 4 5 1 • layout the k heavest nodes in order of decreasing size • recurse on subtrees in order of decreasing size • a search uses O (log Bα +1 n ) I/Os Skewed Binary Search Trees 24

Blocked Layouts — veb top 15 6 5 9 2 10 3 1 5 1 3 7 12 3 2 2 1 3 4 8 11 13 2 1 1 5 9 14 15 1 6 10 2 12 13 14 15 7 8 9 3 4 5 11 1 • top = ⌈√ n ⌉ heavest nodes • recurse on top and bottom trees in order of decreasing size • a search uses O (log Bα +1 n ) I/Os Skewed Binary Search Trees 25

Running Time for Blocked Layouts 0.22 DFSr 0.21 vEB bDFS 0.2 pqDFS Running time 0.19 0.18 0.17 0.16 0.15 0.14 0.13 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 α vEB achieves the fastest running time for α ≈ . 25 Skewed Binary Search Trees 26

Cache Faults for Blocked Layouts 1e+07 DFSr vEB bDFS 8e+06 pqDFS Cache misses 6e+06 4e+06 2e+06 0 0 0.2 0.4 0.6 0.8 1 α vEB achieves the smallest number of cache faults Skewed Binary Search Trees 27

Experimental Summary 3.5e+08 0.22 DFSr 0.21 vEB 3e+08 bDFS 0.2 pqDFS 2.5e+08 Comparisons Running time 0.19 2e+08 0.18 0.17 1.5e+08 0.16 1e+08 0.15 5e+07 0.14 0 0.13 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 α α 8e+06 1e+07 DFSr vEB 7e+06 bDFS Branch mispredictions 8e+06 pqDFS Cache misses 6e+06 6e+06 5e+06 4e+06 4e+06 2e+06 3e+06 2e+06 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0 0.2 0.4 0.6 0.8 1 α α Skewed Binary Search Trees 28

Conclusion Skewed binary search trees beat Perfectly balanced binary search trees because The costs going left and right are different ! Skewed Binary Search Trees 29