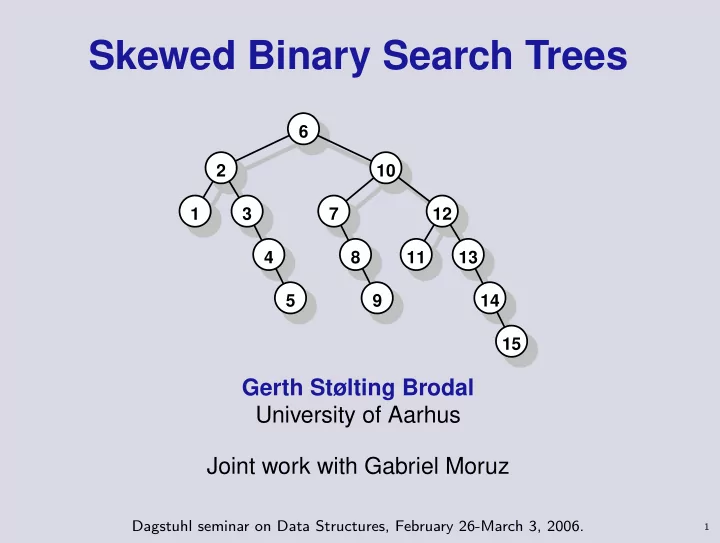
Skewed Binary Search Trees 6 2 10 1 3 7 12 4 8 11 13 5 9 - PowerPoint PPT Presentation

Skewed Binary Search Trees 6 2 10 1 3 7 12 4 8 11 13 5 9 14 15 Gerth Stølting Brodal University of Aarhus Joint work with Gabriel Moruz Dagstuhl seminar on Data Structures, February 26-March 3, 2006. 1

Skewed Binary Search Trees 6 2 10 1 3 7 12 4 8 11 13 5 9 14 15 Gerth Stølting Brodal University of Aarhus Joint work with Gabriel Moruz in progress Dagstuhl seminar on Data Structures, February 26-March 3, 2006. 1

Perfectly Balanced Search Trees 8 4 12 2 6 10 14 1 3 5 7 9 11 13 15 Skewed Binary Search Trees 2

Skewed Binary Search Trees x α ⌊ α ( n − 1) ⌋ 1 − α ⌈ (1 − α )( n − 1) ⌉ Skewed Binary Search Trees 3

Skewed Binary Search Trees 8 4 12 2 6 10 14 1 3 5 7 9 11 13 15 α = 0 . 5 Skewed Binary Search Trees 4

Skewed Binary Search Trees 6 2 10 1 3 7 12 4 8 11 13 5 9 14 15 α = 0 . 4 Skewed Binary Search Trees 5

Skewed Binary Search Trees 3 1 6 2 4 8 5 7 10 9 11 12 α = 0 . 2 13 14 15 Skewed Binary Search Trees 6

Skewed Binary Search Trees 1 2 3 4 5 6 7 8 9 10 11 12 α = 0 . 05 13 14 15 Skewed Binary Search Trees 7

Skewed Binary Search Trees — Average Node Depth 1 · n + 1 ≤ · log 2 ( n + 1) − 2 − α log 2 α − (1 − α ) log 2 (1 − α ) n � �� � H ( α ) Nievergelt and E. M. Reingold, 1972 Skewed Binary Search Trees 8

H ( α ) 10 8 6 H ( α ) 4 2 0 0 0.2 0.4 0.6 0.8 1 α Skewed Binary Search Trees 9

Comparisons 300 250 Comparisons 200 150 100 50 0 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 α n = 20 . 000 Skewed Binary Search Trees 10

Running Time 0.15 0.145 Running time, 10 − 6 sec 0.14 0.135 0.13 0.125 0.12 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 α Best running time achieved for α ≈ 0 . 3 !? Skewed Binary Search Trees 11

Conclusion Skewed binary search trees beat Perfectly balanced binary search trees ! Skewed Binary Search Trees 12

Conclusion Skewed binary search trees n a c beat Perfectly balanced binary search trees ! Skewed Binary Search Trees 12

Why ? Skewed Binary Search Trees 13

Why ? The costs going left and right are different ! Possible reasons • Number of instructions • Branch mispredictions • Cache faults (what is a good memory layout?) • ... Skewed Binary Search Trees 14

Expected Cost cost ( α ) = ( α · {left cost} + (1 − α ) · {right cost} ) · H ( α ) 8 7 6 5 cost ( α ) 4 3 2 1 0 0 0.2 0.4 0.6 0.8 1 α left cost = 1 and right cost = 3 Skewed Binary Search Trees 15

Expected Cost cost ( α ) = ( α · {left cost} + (1 − α ) · {right cost} ) · H ( α ) 8 7 6 5 cost ( α ) 4 3 2 1 0 0 0.2 0.4 0.6 0.8 1 α left cost = 1 and right cost = 0 .. 28 Skewed Binary Search Trees 16

Search Code int search(int root, int key) { if (root==NULLV) return NULLV; if (key==t[root].key) return root; if(key>t[root].key) return search(t[root].right, key); else return search(t[root].left, key); } Skewed Binary Search Trees 17

Branch Mispredictions 22 20 Branch mispredictions 18 16 14 12 10 8 6 4 2 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 α Static branch prediction: left cost = 1 and right cost = 0 Skewed Binary Search Trees 18

Simple Layouts 4 5 1 7 6 2 3 3 Random 1 5 1 2 3 4 5 6 7 Inorder 2 4 6 3 1 5 2 4 6 7 7 BFS 3 5 6 7 4 1 2 DFS Skewed Binary Search Trees 19

Running Time for Simple Layouts 0.35 DFSl DFSr Running time, 10 − 6 sec 0.3 BFS Random Inorder 0.25 0.2 0.15 0.1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 α DFS < Inorder < BFS < Random DFS achieves the best performance for α ≈ 0 . 2 ! Skewed Binary Search Trees 20

Cache Faults for Simple Layouts 14 DFSl DFSr 12 BFS Random Inorder 10 Cache faults 8 6 4 2 0 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 α 1 DFS ≈ expected left cost = 1 and right cost = cache-line size Skewed Binary Search Trees 21

Blocked Layouts — pqDFS k 15 6 5 9 2 10 3 1 5 1 3 7 12 3 3 2 2 1 4 8 11 13 2 1 1 5 9 14 k = 3 15 1 6 10 2 12 13 14 15 11 7 8 9 3 4 5 1 • layout the k heavest nodes in order of decreasing size • recurse on subtrees in order of decreasing size Skewed Binary Search Trees 22

Blocked Layouts — veb top 15 6 5 9 2 10 3 1 5 1 3 7 12 3 2 2 1 3 4 8 11 13 2 1 1 5 9 14 15 1 6 10 2 12 13 14 15 7 8 9 3 4 5 11 1 • top = ⌈√ n ⌉ heavest nodes • recurse on top and bottom trees in order of decreasing size Skewed Binary Search Trees 23

Running Time for Blocked Layouts 0.2 DFSr 0.19 pqDFS2 Running time, 10 − 6 sec pqDFS4 0.18 pqDFS8 vEB 0.17 0.16 0.15 0.14 0.13 0.12 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 α Skewed Binary Search Trees 24

Cache Faults for Blocked Layouts 5 DFSr 4.5 pqDFS2 pqDFS4 pqDFS8 4 vEB Cache faults 3.5 3 2.5 2 1.5 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 α Skewed Binary Search Trees 25

Experimental Summary 300 0.2 DFSr 0.19 pqDFS2 250 Running time, 10 − 6 sec pqDFS4 0.18 pqDFS8 Comparisons vEB 200 0.17 150 0.16 0.15 100 0.14 50 0.13 0 0.12 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 α α 22 5 20 DFSr 4.5 pqDFS2 Branch mispredictions 18 pqDFS4 pqDFS8 4 16 vEB Cache faults 14 3.5 12 3 10 8 2.5 6 2 4 2 1.5 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 α α Skewed Binary Search Trees 26

Conclusion Skewed binary search trees n a c beat Perfectly balanced binary search trees because The costs going left and right are different ! Skewed Binary Search Trees 27

Questions • Can we give a precise theoretical explanation of the experimental results ? • Different values of n ? • Different computer architectures ? • What is the best layout of a tree on a given machine ? • What is the best tree ? • ... 6 2 10 1 3 7 12 4 8 11 13 5 9 14 15 Skewed Binary Search Trees 28

Experimental setup • AMD Athlon XP 2400+ • 2.0 GHz • 256 Kb L2 cache • 64 Kb L1 data cache • 64 Kb L1 instruction cache • 1Gb RAM • Linux 2.6.8.1 • GCC 3.3.2 • Tree nodes = 12 bytes Skewed Binary Search Trees 29