! Single Layer Recurrent Network ! Bidirectional Symmetric - PowerPoint PPT Presentation

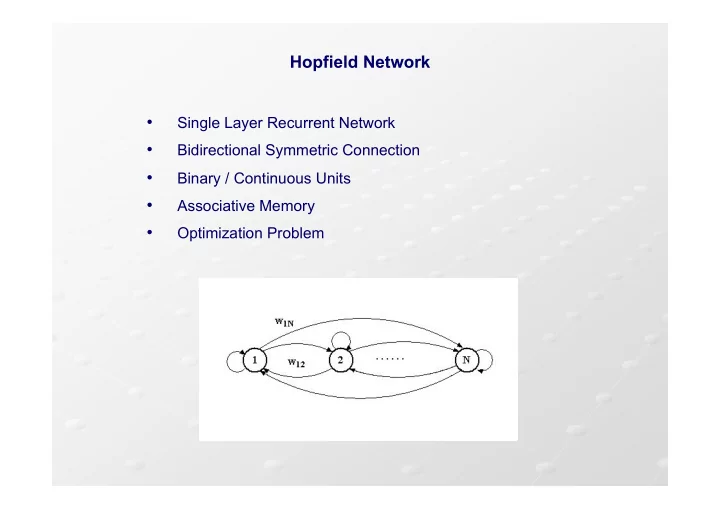
Hopfield Network • ! Single Layer Recurrent Network • ! Bidirectional Symmetric Connection • ! Binary / Continuous Units • ! Associative Memory • ! Optimization Problem

Hopfield Model – Discrete Case Recurrent neural network that uses McCulloch and Pitt’s (binary) neurons. Update rule is stochastic. Eeach neuron has two “states” : V i L , V i H V i L = -1 , V i H = 1 Usually : V i L = 0 , V i H = 1 Input to neuron i is : Where: • ! w ij = strength of the connection from j to i • ! V j = state (or output) of neuron j • ! I i = external input to neuron i

Hopfield Model – Discrete Case Each neuron updates its state in an asynchronous way, using the following rule: The updating of states is a stochastic process: To select the to-be-updated neurons we can proceed in either of two ways: • ! At each time step select at random a unit i to be updated (useful for simulation) • ! Let each unit independently choose to update itself with some constant probability per unit time (useful for modeling and hardware implementation)

Dynamics of Hopfield Model In contrast to feed-forward networks (wich are “static”) Hopfield networks are dynamical system. The network starts from an initial state V(0) = ( V 1 (0), ….. ,V n (0) ) T and evolves in state space following a trajectory: Until it reaches a fixed point: V(t+1) = V(t)

Dynamics of Hopfield Networks What is the dynamical behavior of a Hopfield network ? Does it coverge ? Does it produce cycles ? Examples (a) (b)

Dynamics of Hopfield Networks To study the dynamical behavior of Hopfield networks we make the following assumption: In other words, if W = ( w ij ) is the weight matrix we assume: In this case the network always converges to a fixed point. In this case the system posseses a Liapunov (or energy) function that is minimized as the process evolves.

The Energy Function – Discrete Case Consider the following real function: and let Assuming that neuron h has changed its state, we have: But and have the same sign. Hence (provided that )

Schematic configuration space model with three attractors

Hopfield Net As Associative Memory Store a set of p patterns x ! , ! = 1,…, p ,in such a way that when presented with a new pattern x , the network responds by producing that stored pattern which most closely resembles x. • ! N binary units, with outputs s 1 ,…, s N • ! Stored patterns and test patterns are binary (0/1,±1) • ! Connection weights (Hebb Rule) Hebb suggested changes in synaptic strengths proportional to the correlation between the firing of the pre and post-synaptic neurons. • ! Recall mechanism Synchronous / Asynchronous updating • ! Pattern information is stored in equilibrium states of the network

Example With Two Patterns • ! Two patterns X 1 = (-1,-1,-1,+1) X 2 = (+1,+1,+1,+1) • ! Compute weights • ! Weight matrix • ! Recall • ! Input (-1,-1,-1,+1) ! (-1,-1,-1,+1) stable • ! Input (-1,+1,+1,+1) ! (+1,+1,+1,+1) stable • ! Input (-1,-1,-1,-1) ! (-1,-1,-1,-1) spurious

Associative Memory Examples An example of the behavior of a Hopfield net when used as a content-addressable memory. A 120 node net was trained using the eight examplars shown in (A). The pattern for the digit “3” was corrupted by randomly reversing each bit with a proba- bility of 0.25 and then applied to the net at time zero. Outputs at time zero and after the first seven iterations are shown in (B).

Associative Memory Examples Example of how an associative memory can reconstruct images. These are binary images with 130 x 180 pixels. The images on the right were recalled by the memory after presentation of the corrupted images shown on the left. The middle column shows some intermediate states. A sparsely connected Hopfield network with seven stored images was used.

Storage Capacity of Hopfield Network • ! There is a maximum limit on the number of random patterns that a Hopfield network can store P max " 0.15 N If p < 0.15 N, almost perfect recall • ! If memory patterns are orthogonal vectors instead of random patterns, then more patterns can be stored. However, this is not useful. • ! Evoked memory is not necessarily the memory pattern that is most similar to the input pattern • ! All patterns are not remembered with equal emphasis, some are evoked inappropriately often • ! Sometimes the network evokes spurious states

Hopfield Model – Continuous Case The Hopfield model can be generalized using continuous activation functions. More plausible model. In this case: where is a continuous, increasing, non linear function. Examples

Funzione di attivazione +1 -1

Updating Rules Several possible choices for updating the units : Asynchronous updating: one unit at a time is selected to have its output set Synchronous updating: at each time step all units have their output set Continuous updating: all units continuously and simultaneously change their outputs

Continuous Hopfield Models Using the continuous updating rule, the network evolves according to the following set of (coupled) differential equations: where are suitable time constants ( > 0). Note When the system reaches a fixed point ( / = 0 ) we get Indeed, we study a very similar dynamics

The Energy Function As the discrete model, the continuous Hopfield network has an “energy” function, provided that W = W T : Easy to prove that with equality iff the net reaches a fixed point.

Modello di Hopfield continuo (energia) Perché è monotona crescente e . N.B. cioè è un punto di equilibrio

Modello di Hopfield continuo (relazione con il modello discreto) Esiste una relazione stretta tra il modello continuo e quello discreto. Si noti che : quindi : Il 2 o termine in E diventa : L’integrale è positivo (0 se V i =0). Per il termine diventa trascurabile, quindi la funzione E del modello continuo diventa identica a quello del modello discreto

Optimization Using Hopfield Network ! ! Energy function of Hopfield network ! ! The network will evolve into a (locally / globally) minimum energy state ! ! Any quadratic cost function can be rewritten as the Hopfield network Energy function. Therefore, it can be minimized using Hopfield network. ! ! Classical Traveling Salesperson Problem (TSP) ! ! Many other applications • ! 2-D, 3-D object recognition • ! Image restoration • ! Stereo matching • ! Computing optical flow

The Traveling Salesman Problem Problem statement: A travelling salesman must visit every city in his territory exactly once and then return to his starting point. Given the cost of travel between all pairs of cities, find the minimum cost tour. ! ! NP-Complete Problem ! ! Exhaustive Enumeration: nodes, enumerations, distinct enumerations distinct undirected enumerations Example: n = 10, 19!/2 = 1.2 x 10 18

The Traveling Salesman Problem TSP: find the shortest tour connecting a set of cities. Following Hopfield & Tank (1985) a tour can be represented by a permutation matrix:

The Traveling Salesman Problem The TSP, showing a good (a) and a bad (b) solution to the same problem Network to solve a four-city TSP. Solid and open circles denote units that are on and off respectively when the net is representing the tour 3-2-4-1. The connections are shown only for unit n 22 ; solid lines are inhibitory connections of strength –d ij , and dotted lines are uni- form inhibitory connections of strength – # . All connections are symmetric. Thresholds are not shown.

Artificial Neural Network Solution Solution to n -city problem is presented in an n x n permutation matrix V X = city i = stop at wich the city is visited Voltage output: V X,i Connection weights: T Xi,Yj n 2 neurons V X,i = 1 if city X is visited at stop i d XY = distance between city X and city Y

Artificial Neural Network Solution • ! Data term: We want to minimize the total distance • ! Constraint terms: Each city must be visited once Each stop must contain one city The matrix must contain n entries

Artificial Neural Network Solution • ! A, B, C, and D are positive constants • ! Indici modulo n Total cost function La funzione energia della rete di Hopfield è:

Network Weights The coefficients of the quadratic terms in the cost function define the weights of the connections in the network {Inhibitory connection in each row} {Inhibitory connection in each column} {Global inhibition} {Data term} {External current}

Experiments • ! 10-city problem, 100 neurons • ! Locations of the 10 cities are chosen randomly with uniform p.d.f. in unit square • ! Parameters: A = B = 500, C = 200, D = 500 • ! The size of the squares correspond to the value of the voltage output at the corresponding neurons. • ! Path: D-H-I-F-G-E-A-J-C-B

TSP – A Second Formulation Another way of formulating the TSP constraints (i.e., permutation matrix) is the following row constraint column constraint The energy function becomes : Advantage : less parameters (A,B,D)

The N-queen Problem Build an n x n network whose neuron ( i , j ) is active if and only if a queen occupies position ( i , j ) There are 4 constraints : 1. ! Only one queen on each row 2. ! Only one queen on each column 3. ! Only one queen on each diagonal 4. ! Exactly n queens on the chessboard