Semantics + What is meaning of 3+5*6 ? * 3 First parse it into - PDF document

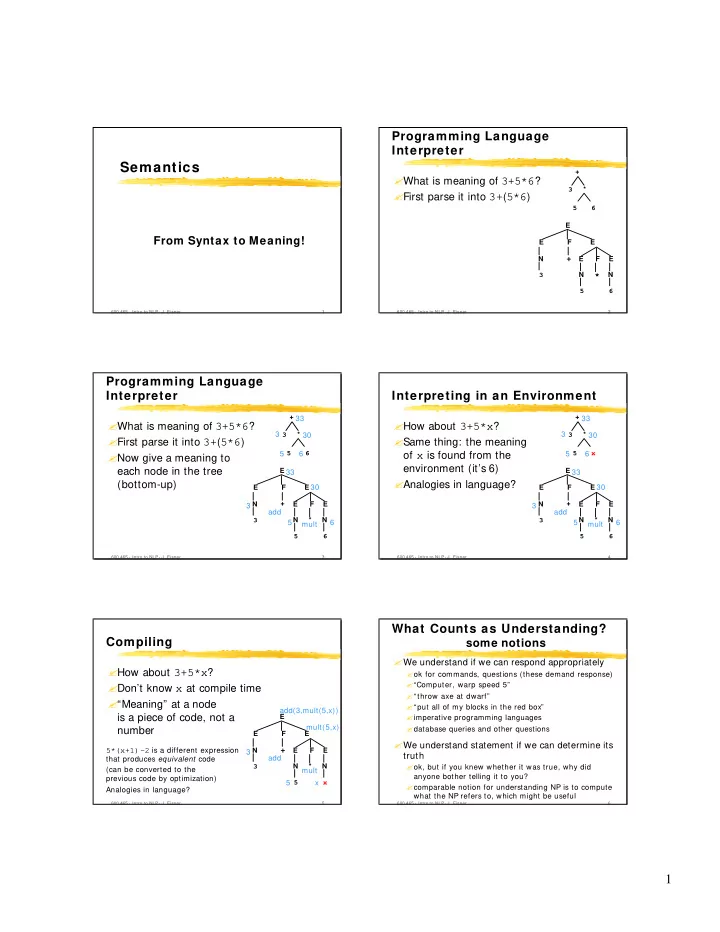
Programming Language Interpreter Semantics + � What is meaning of 3+5*6 ? * 3 � First parse it into 3+ ( 5*6 ) 5 6 E From Syntax to Meaning! E F E N + E F E 3 N N * 5 6 600.465 - Intro to NLP - J. Eisner 1 600.465 - Intro to NLP - J. Eisner 2 Programming Language Interpreter Interpreting in an Environment + + 33 33 � What is meaning of 3+5*6 ? � How about 3+5*x ? 3 * 3 * 3 30 3 30 � First parse it into 3+ ( 5*6 ) � Same thing: the meaning � Now give a meaning to 5 5 6 6 of x is found from the 5 5 6 x environment (it’s 6) each node in the tree E E 33 33 � Analogies in language? (bottom-up) E F E 30 E F E 30 + + N E F E N E F E 3 3 add add N * N N * N 3 3 5 6 5 6 mult mult 5 6 5 6 600.465 - Intro to NLP - J. Eisner 3 600.465 - Intro to NLP - J. Eisner 4 What Counts as Understanding? Compiling some notions � We understand if we can respond appropriately � How about 3+5*x ? � ok for commands, questions (these demand response) � “Computer, warp speed 5” � Don’t know x at compile time � “throw axe at dwarf” � “Meaning” at a node � “put all of my blocks in the red box” add(3,mult(5,x)) is a piece of code, not a � imperative programming languages E mult(5,x) � database queries and other questions number E F E � We understand statement if we can determine its 5*(x+1)-2 is a different expression N + E F E 3 truth add that produces equivalent code � ok, but if you knew whether it was true, why did N * N 3 (can be converted to the mult anyone bother telling it to you? previous code by optimization) 5 x 5 x � comparable notion for understanding NP is to compute Analogies in language? what the NP refers to, which might be useful 600.465 - Intro to NLP - J. Eisner 5 600.465 - Intro to NLP - J. Eisner 6 1

What Counts as Understanding? What Counts as Understanding? some notions some notions � Be able to translate � We understand statement if we know how to determine its truth � Depends on target language � What are exact conditions under which it would be true? � English to English? bah humbug! � necessary + sufficient � English to French? � Equivalently, derive all its consequences reasonable � what else must be true if we accept the statement? � English to Chinese? requires deeper understanding � Philosophers tend to use this definition � English to logic ? deepest - the definition we’ll use! � We understand statement if we can use it to � all humans are mortal = ? x [human(x) ? mortal(x)] answer questions [very similar to above – requires reasoning] � Easy: John ate pizza. What was eaten by John? � Assume we have logic- manipulating rules to tell us � Hard: White’s first move is P -Q4. Can Black checkmate? how to act, draw conclusions, answer questions … � Constructing a procedure to get the answer is enough 600.465 - Intro to NLP - J. Eisner 7 600.465 - Intro to NLP - J. Eisner 8 Lecture Plan Logic: Some Preliminaries Three major kinds of objects � Today: 1. Booleans � Let’s look at some sentences and phrases � Roughly, the semantic values of sentences � What would be reasonable logical 2. Entities representations for them? � Values of NPs, e.g., objects like this slide � Tomorrow: � Maybe also other types of entities, like times 3. Functions of various types � How can we build those representations? � A function returning a boolean is called a � Another course (AI): “predicate” – e.g., frog(x), green(x) � Functions might return other functions! � How can we reason with those representations? � Function might take other functions as arguments! 600.465 - Intro to NLP - J. Eisner 9 600.465 - Intro to NLP - J. Eisner 10 Logic: Lambda Terms Logic: Lambda Terms � Lambda terms: � Lambda terms: � Let square = ? p p* p � A way of writing “anonymous functions” � Then square(3) = ( ? p p* p)(3) = 3* 3 � No function header or function name � Note: square(x) isn’t a function! It’s just the value x* x. � But defines the key thing: behavior of the function � But ? x square(x) = ? x x* x = ? p p* p = square � Just as we can talk about 3 without naming it “x” (proving that these functions are equal – and indeed they are, as they act the same on all arguments: what is ( ? x square(x))(y)? ) � Let square = ? p p* p � Let even = ? p (p mod 2 = = 0) a predicate: returns true/false � Equivalent to int square(p) { return p* p; } � even(x) is true if x is even � But we can talk about ? p p* p without naming it � How about even(square(x))? � Format of a lambda term: ? variable expression � ? x even(square(x)) is true of numbers with even squares � Just apply rules to get ? x (even(x* x)) = ? x (x* x mod 2 = = 0) � This happens to denote the same predicate as even does 600.465 - Intro to NLP - J. Eisner 11 600.465 - Intro to NLP - J. Eisner 12 2

Logic: Multiple Arguments Logic: Multiple Arguments � All lambda terms have one argument � All lambda terms have one argument � But we can fake multiple arguments ... � But we can fake multiple arguments ... � Claim that times(5)(6) means same as times(5,6) � Suppose we want to write times(5,6) � times(5) = ( ? x ? y times(x,y )) (5) = ? y times(5,y) � Remember: square can be written as ? x square(x) � If this function weren’t anonymous, what would we call it? � Similarly, times is equivalent to ? x ? y times(x,y) � times(5)(6) = ( ? y times(5,y))(6) = times(5,6) � So we can always get away with 1-arg functions ... � Claim that times(5)(6) means same as times(5,6) � ... which might return a function to take the next � times(5) = ( ? x ? y times(x,y )) (5) = ? y times(5,y) argument. Whoa. � If this function weren’t anonymous, what would we call it? � times(5)(6) = ( ? y times(5,y))(6) = times(5,6) � We’ll still allow times(x,y ) as syntactic sugar, though 600.465 - Intro to NLP - J. Eisner 13 600.465 - Intro to NLP - J. Eisner 14 Grounding out Logic: Interesting Constants � Thus, have “constants” that name some of � So what does times actually mean??? � How do we get from times(5,6) to 30 ? the entities and functions (e.g., times): � Whether times(5,6) = 30 depends on whether symbol times � GeorgeWBush - an entity actually denotes the multiplication function! � red – a predicate on entities � Well, maybe times was defined as another lambda term, � holds of just the red entities: red(x) is true if x is red! so substitute to get times(5,6) = (blah blah blah )(5)(6) � loves – a predicate on 2 entities � loves(GeorgeWBush, LauraBush) � But we can’t keep doing substitutions forever! � Question: What does loves(LauraBush ) denote? � Eventually we have to ground out in a primitive term � Constants used to define meanings of words � Primitive terms are bound to object code � Maybe times(5,6) just executes a multiplication function � Meanings of phrases will be built from the � What is executed by loves(john, mary ) ? constants 600.465 - Intro to NLP - J. Eisner 15 600.465 - Intro to NLP - J. Eisner 16 A reasonable representation? Logic: Interesting Constants � most – a predicate on 2 predicates on � Gilly swallowed a goldfish entities � First attempt: swallowed(Gilly, goldfish) � most(pig, big) = “ most pigs are big” � Equivalently, most( ? x pig(x), ? x big(x)) � Returns true or false. Analogous to � returns true if most of the things satisfying the first predicate also satisfy the second predicate � prime(17) � similarly for other quantifiers � equal(4,2+ 2) � all(pig,big) (equivalent to ? x pig(x) ? � loves(GeorgeWBush, LauraBush) big(x) ) � exists(pig,big) (equivalent to ? x pig(x) AND big(x) ) � swallowed(Gilly, Jilly) � can even build complex quantifiers from English phrases: � … or is it analogous? � “between 12 and 75”; “a majority of ”; “all but the smallest 2” 600.465 - Intro to NLP - J. Eisner 17 600.465 - Intro to NLP - J. Eisner 18 3