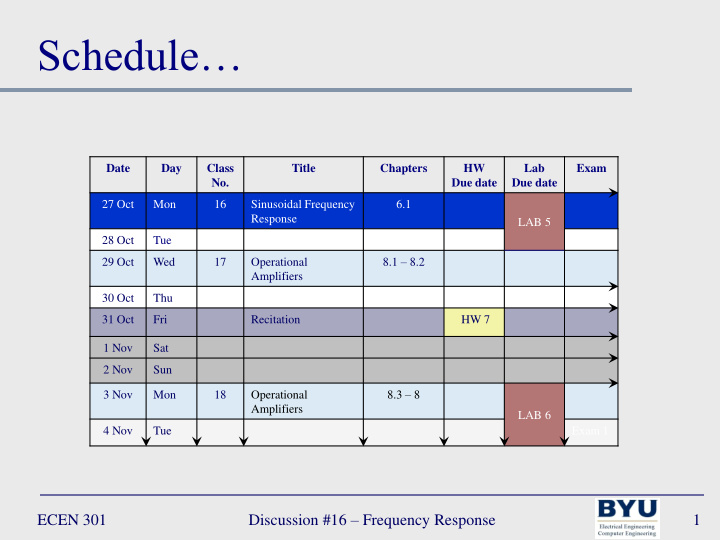
Schedule Date Day Class Title Chapters HW Lab Exam No. Due - PowerPoint PPT Presentation

Schedule… Date Day Class Title Chapters HW Lab Exam No. Due date Due date 27 Oct Mon 16 Sinusoidal Frequency 6.1 Response LAB 5 28 Oct Tue 8.1 – 8.2 29 Oct Wed 17 Operational Amplifiers 30 Oct Thu 31 Oct Fri Recitation HW 7 1 Nov Sat 2 Nov Sun 8.3 – 8 3 Nov Mon 18 Operational Amplifiers LAB 6 4 Nov Tue Exam 1 Discussion #16 – Frequency Response ECEN 301 1

Easier to Maintain Than to Retake Alma 59:9 9 And now as Moroni had supposed that there should be men sent to the city of Nephihah, to the assistance of the people to maintain that city, and knowing that it was easier to keep the city from falling into the hands of the Lamanites than to retake it from them , he supposed that they would easily maintain that city. Discussion #16 – Frequency Response ECEN 301 2

Lecture 16 – Frequency Response Back to AC Circuits and Phasors • Frequency Response • Filters Discussion #16 – Frequency Response ECEN 301 3

Frequency Response Frequency Response H(j ω ): a measure of how the voltage/current/impedance of a load responds to the voltage/current of a source   ( ) ( ) V j I j     ( ) ( ) L L H j H j   V I ( ) ( ) V j I j S S  ( ) V j   ( ) L H j  Z ( ) I j S Discussion #16 – Frequency Response ECEN 301 4

Frequency Response V L (j ω ) is a phase-shifted and amplitude-scaled version of V S (j ω )  ( ) V j   L ( ) H j  V ( ) V j S     ( ) ( ) ( ) V j H j V j L V S Discussion #16 – Frequency Response ECEN 301 5

Frequency Response V L (j ω ) is a phase-shifted and amplitude-scaled version of V S (j ω )  ( ) V j : any complex number NB   L ( ) H j  V ( ) V j can be expressed as A S       j A ( ) ( ) ( ) V j H j V j A A e L V S       j j H j V A A A V e H e V e L V S L V S      ( ) j j H V V e H V e L V S L V S      V  H V H V L V S L V S Amplitude scaled Phase shifted Discussion #16 – Frequency Response ECEN 301 6

Frequency Response Example1 : compute the frequency response H V (j ω ) R 1 = 1k Ω , R L = 10k Ω , C = 10uF R 1 + + v s (t) C R L – – Discussion #16 – Frequency Response ECEN 301 7

Frequency Response Example1 : compute the frequency response H V (j ω ) R 1 = 1k Ω , R L = 10k Ω , C = 10uF R 1 1. Note frequencies of AC sources + Only one AC source so frequency + v s (t) C response H V (j ω ) will be the R L – – function of a single frequency Discussion #16 – Frequency Response ECEN 301 8

Frequency Response Example1 : compute the frequency response H V (j ω ) R 1 = 1k Ω , R L = 10k Ω , C = 10uF 1. Note frequencies of AC sources 2. Convert to phasor domain Z 1 = R 1 R 1 Z C =1/j ω C + + + V s v s (t) C R L ~ Z LD =R L – – – Discussion #16 – Frequency Response ECEN 301 9

Frequency Response Example1 : compute the frequency response H V (j ω ) R 1 = 1k Ω , R L = 10k Ω , C = 10uF 1. Note frequencies of AC sources 2. Convert to phasor domain Z 1 = R 1 3. Solve using network analysis • Thévenin equivalent Z C =1/j ω C  || Z Z Z 1 T C Discussion #16 – Frequency Response ECEN 301 10

Frequency Response Example1 : compute the frequency response H V (j ω ) R 1 = 1k Ω , R L = 10k Ω , C = 10uF 1. Note frequencies of AC sources 2. Convert to phasor domain Z 1 = R 1 3. Solve using network analysis • Thévenin equivalent Z C =1/j ω C + + V s ~ V T – Z –    C ( ) ( ) V j V j  T S Z Z 1 C  || Z Z Z 1 T C Discussion #16 – Frequency Response ECEN 301 11

Frequency Response Example1 : compute the frequency response H V (j ω ) R 1 = 1k Ω , R L = 10k Ω , C = 10uF 1. Note frequencies of AC sources Z T 2. Convert to phasor domain 3. Solve using network analysis • Thévenin equivalent + 4. Find an expression for the load voltage + V T V L ~ Z LD – – Z    ( ) ( ) LD V j V j  L T Z Z T LD    || Z Z Z Z Z     1 T C C LD ( ) V j       S   || Z Z Z Z Z Z    1 1 C C LD ( ) ( ) C V j V j  T S Z Z 1 C Discussion #16 – Frequency Response ECEN 301 12

Frequency Response Example1 : compute the frequency response H V (j ω ) R 1 = 1k Ω , R L = 10k Ω , C = 10uF 5. Find an expression for the frequency Z T response  + ( ) V j   + ( ) L H j V T V L ~ Z LD  V ( ) V j – – S Z Z   C LD     || Z Z Z Z Z 1 1 C C LD Discussion #16 – Frequency Response ECEN 301 13

Frequency Response Example1 : compute the frequency response H V (j ω ) R 1 = 1k Ω , R L = 10k Ω , C = 10uF 5. Find an expression for the frequency Z T response Z Z    ( ) C LD H j     V || Z Z Z Z Z + 1 1 C C LD + V T Z Z V L ~ Z LD  LD C   –   – Z Z Z Z Z 1 1 LD C C    4 5 10 /( 10 ) j            4 3 5 3 5 10 10 1 /( 10 ) 10 /( 10 ) j j 100    110 j    100      arctan     110 2 2 110 Discussion #16 – Frequency Response ECEN 301 14

Frequency Response Example1 : compute the frequency response H V (j ω ) R 1 = 1k Ω , R L = 10k Ω , C = 10uF 5. Find an expression for the frequency response Z T • Look at response for low frequencies ( ω = 10) and high frequencies ( ω = 10000) +    100 +     V T   V L ( ) arctan ~ Z LD H V j –     – 110 2 2 110 ω = 10000 ω = 10      ( ) 0 . 010     H V j ( ) 0 . 905 0 . 0907 H V j 2 Discussion #16 – Frequency Response ECEN 301 15

Frequency Response Example2 : compute the frequency response H Z (j ω ) R 1 = 1k Ω , R L = 4k Ω , L = 2mH L + i s (t) R L R 1 – Discussion #16 – Frequency Response ECEN 301 16

Frequency Response Example2 : compute the frequency response H Z (j ω ) R 1 = 1k Ω , R L = 4k Ω , L = 2mH 1. Note frequencies of AC sources L Only one AC source so frequency + response H Z (j ω ) will be the i s (t) R L R 1 function of a single frequency – Discussion #16 – Frequency Response ECEN 301 17

Frequency Response Example2 : compute the frequency response H Z (j ω ) R 1 = 1k Ω , R L = 4k Ω , L = 2mH 1. Note frequencies of AC sources 2. Convert to phasor domain Z L = j ω L L I s (j ω ) + + i s (t) V L R L R 1 Z 1 =R 1 Z LD = R L – – Discussion #16 – Frequency Response ECEN 301 18

Frequency Response Example2 : compute the frequency response H Z (j ω ) R 1 = 1k Ω , R L = 4k Ω , L = 2mH 1. Note frequencies of AC sources 2. Convert to phasor domain Z L = j ω L 3. Solve using network analysis • Current divider & Ohm’s Law I L (j ω )  I s (j ω ) || ( ) Z Z Z +    1 ( ) ( ) L LD I j I j  V L L S ( ) Z 1 =R 1 Z Z Z LD = R L – L LD    ( ) ( ) V j I j Z L L LD    || ( ) Z Z Z     1 ( ) L LD I j Z    S LD  ( )  Z Z L LD Discussion #16 – Frequency Response ECEN 301 19

Frequency Response Example2 : compute the frequency response H Z (j ω ) R 1 = 1k Ω , R L = 4k Ω , L = 2mH 4. Find an expression for the frequency response Z L = j ω L  ( ) V j   ( ) L H j  I L (j ω ) Z ( ) I j I s (j ω ) S +  || ( ) Z Z Z  V L 1 L LD Z Z 1 =R 1 Z LD = R L  LD – ( ) Z Z L LD R  L    1 / / R R j L R 1 1 L 800      6 1 0 . 4 10 j Discussion #16 – Frequency Response ECEN 301 20

Frequency Response Example2 : compute the frequency response H Z (j ω ) R 1 = 1k Ω , R L = 4k Ω , L = 2mH 4. Find an expression for the frequency response • Look at response for low frequencies ( ω = 10) Z L = j ω L and high frequencies ( ω = 10000) I L (j ω ) 800 I s (j ω )   + ( ) H Z j     6 1 0 . 4 10 V L j Z 1 =R 1 Z LD = R L – ω = 10000 ω = 10         ( ) 800 0 . 0040 ( ) 800 4 . 0 H Z j H Z j Discussion #16 – Frequency Response ECEN 301 21

1 st and 2 nd Order RLC Filters Graphing in Frequency Domain Filter Orders Resonant Frequencies Basic Filters Discussion #16 – Frequency Response ECEN 301 22

Frequency Domain Graphing in the frequency domain: helpful in order to understand filters 1.5 3.50 π π X(jw) x(t) 0.0 0.00 2.00 4.00 0.00 - ω ω -600.0 0.0 600.0 -1.5 w time π [ δ ( ω – ω 0 ) + δ ( ω – ω 0 )] cos( ω 0 t) Time domain Frequency domain Discussion #16 – Frequency Response ECEN 301 23

Frequency Domain Graphing in the frequency domain: helpful in order to understand filters W/ π 1 X(jw) π /W x(t) 0.0 -10.00 0.00 10.00 -W W -0.5 -10.00 0.00 10.00 w t    1 , | | W sinc( ω 0 t)    ( ) X j    0 , | | W Time domain Frequency domain Discussion #16 – Frequency Response ECEN 301 24