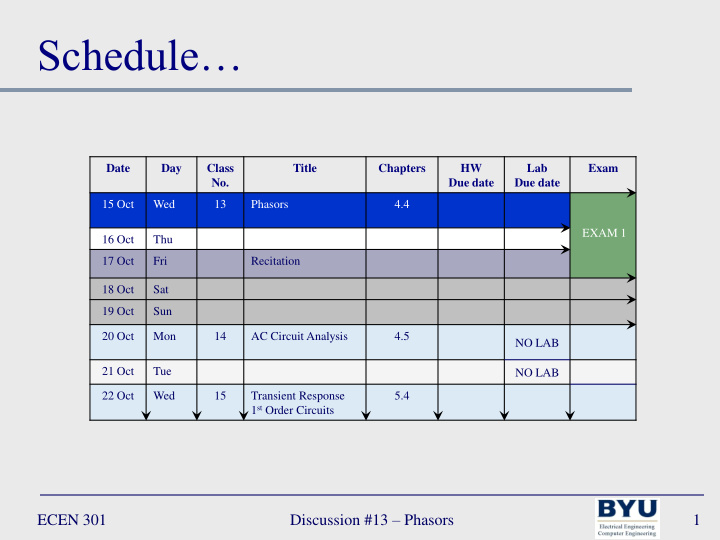
Schedule Date Day Class Title Chapters HW Lab Exam No. Due - PowerPoint PPT Presentation

Schedule… Date Day Class Title Chapters HW Lab Exam No. Due date Due date 15 Oct Wed 13 Phasors 4.4 EXAM 1 16 Oct Thu 17 Oct Fri Recitation 18 Oct Sat 19 Oct Sun 20 Oct Mon 14 AC Circuit Analysis 4.5 NO LAB 21 Oct Tue NO LAB 22 Oct Wed 15 Transient Response 5.4 1 st Order Circuits Discussion #13 – Phasors ECEN 301 1

Imaginary JS-H 1: 16 16 But, exerting all my powers to call upon God to deliver me out of the power of this enemy which had seized upon me, and at the very moment when I was ready to sink into despair and abandon myself to destruction — not to an imaginary ruin, but to the power of some actual being from the unseen world, who had such marvelous power as I had never before felt in any being — just at this moment of great alarm, I saw a pillar of light exactly over my head, above the brightness of the sun, which descended gradually until it fell upon me. Discussion #13 – Phasors ECEN 301 2

Lecture 13 – Network Analysis with Capacitors and Inductors Phasors Discussion #13 – Phasors ECEN 301 3

Euler’s Identity  Appendix A reviews complex numbers Im Complex exponential ( e j θ ) is a j e j θ point on the complex plane 1 sin θ θ Re -1 1 cos θ      j cos sin -j j e            2 2 j 1 cos sin cos sin 1 e j      j cos sin Ae A jA    A Discussion #13 – Phasors ECEN 301 4

Phasors  Rewrite the expression for a general sinusoid signal :        ( ) t j cos( ) Re{ } A t A e magnitude Angle (or argument) Complex phasor notation for the simplification :    )      j cos( A t A Ae NB : The e jwt term is implicit (it is there but not written) Discussion #13 – Phasors ECEN 301 5

Frequency Domain Graphing in the frequency domain: helpful in order to understand Phasors 1.5 3.50 π π X(jw) x(t) 0.0 0.00 2.00 4.00 0.00 - ω ω -600.0 0.0 600.0 -1.5 w time π [ δ ( ω – ω 0 ) + δ ( ω – ω 0 )] cos( ω 0 t) Time domain Frequency domain Discussion #16 – Frequency Response ECEN 301 6

Electromagnetic Spectrum Discussion #13 – Phasors ECEN 301 7

Phasors 1. Any sinusoidal signal can be represented by either:  Time-domain form : v(t) = Acos( ω t+ θ )  Frequency-domain form : V(j ω ) = Ae j θ = A θ 2. Phasor : a complex number expressed in polar form consisting of:  Magnitude (A)  Phase angle ( θ ) 3. Phasors do not explicitly include the sinusoidal frequency ( ω ) but this information is still important Discussion #13 – Phasors ECEN 301 8

Phasors  Example1 : compute the phasor voltage for the equivalent voltage v s (t)  v 1 (t) = 15cos(377t+ π /4)  v 2 (t) = 15cos(377t+ π /12) + v 1 (t) ~ – + v 2 (t) ~ – + v s (t) ~ – Discussion #13 – Phasors ECEN 301 9

Phasors  Example1 : compute the phasor voltage for the equivalent voltage v s (t)  v 1 (t) = 15cos(377t+ π /4)  v 2 (t) = 15cos(377t+ π /12) 1. Write voltages in phasor notation + v 1 (t) ~ –    / 4 j ( ) 15 V j e + 1 v 2 (t) ~ –    15 V 4    / 12 j ( ) 15 V j e 2    15 V + v s (t) ~ 12 – Discussion #13 – Phasors ECEN 301 10

Phasors  Example1 : compute the phasor voltage for the equivalent voltage v s (t)  v 1 (t) = 15cos(377t+ π /4)  v 2 (t) = 15cos(377t+ π /12) 1. Write voltages in phasor notation + v 1 (t) ~ 2. Convert phasor voltages from polar to – rectangular form (see Appendix A) + v 2 (t) ~ –         ( ) 15 ( ) 15 V j V V j V 2 1 12 4 Convert to rectangula r : Convert to rectangula r :                           ( ) 15 cos 15 sin ( ) 15 cos 15 sin V j j V j j 1 2         4 4 12 12 +     10 . 61 10 . 61 14 . 49 3 . 88 v s (t) j V j V ~ – Discussion #13 – Phasors ECEN 301 11

Phasors  Example1 : compute the phasor voltage for the equivalent voltage v s (t)  v 1 (t) = 15cos(377t+ π /4)  v 2 (t) = 15cos(377t+ π /12) 1. Write voltages in phasor notation + v 1 (t) ~ 2. Convert phasor voltages from polar to – rectangular form (see Appendix A) + 3. Combine voltages v 2 (t) ~ –      ( ) ( ) ( ) V S j V j V j 1 2   25 . 10 14 . 49 j + v s (t) ~ – Discussion #13 – Phasors ECEN 301 12

Phasors  Example1 : compute the phasor voltage for the equivalent voltage v s (t)  v 1 (t) = 15cos(377t+ π /4) 1. Write voltages in phasor notation  v 2 (t) = 15cos(377t+ π /12) 2. Convert phasor voltages from polar to rectangular form (see Appendix A) + 3. Combine voltages v 1 (t) ~ – 4. Convert rectangular back to polar    ( ) 25 . 10 14 . 49 V j j + S v 2 (t) ~ – Convert to polar :   2 2 r (25.10) (14.49)  28 . 98   14 . 49    1   tan   25 . 10   + v s (t) ~ 6 –     ( ) 28 . 98 V j S 6 Discussion #13 – Phasors ECEN 301 13

Phasors  Example1 : compute the phasor voltage for the equivalent voltage v s (t)  v 1 (t) = 15cos(377t+ π /4) 1. Write voltages in phasor notation  v 2 (t) = 15cos(377t+ π /12) 2. Convert phasor voltages from polar to rectangular form (see Appendix A) + 3. Combine voltages v 1 (t) ~ – 4. Convert rectangular back to polar 5. Convert from phasor to time domain + v 2 (t) ~ –     NB : the answer is NOT ( ) 28 . 98 V j S 6 simply the addition of    the amplitudes of v 1 (t)     ( ) 28 . 98 cos 377 v t t and v 2 (t) (i.e. 15 + 15), S   6 and the addition of their phases (i.e. π /4 + π /12) + v s (t) ~ – Bring ω t back Discussion #13 – Phasors ECEN 301 14

Phasors  Example1 : compute the phasor voltage for the equivalent voltage v s (t)  v 1 (t) = 15cos(377t+ π /4)  v 2 (t) = 15cos(377t+ π /12) + v 1 (t) ~ – + v 2 (t) ~ –  Im    ( ) 28 . 98 V j S 6 π /6 Vs(j ω ) 14.49        Re ( ) 28 . 98 cos 377 v t t S   6 + 25.10 v s (t) ~ – Discussion #13 – Phasors ECEN 301 15

Phasors of Different Frequencies Superposition of AC signals : when signals do not have the same frequency ( ω ) the e j ω t term in the phasors can no longer be implicit   ( ) ( ) ( ) i t i t i t I 1 2      ( ) ( ) ( ) I j I j I j + 1 1 2 2     0 0 j j t j j t A e e A e e 1 2 i 1 (t) i 2 (t) v Load 1 2   0 0 j j A e A e – 1 2 NB : e j ω t can no longer be implicit Discussion #13 – Phasors ECEN 301 16

Phasors of Different Frequencies Superposition of AC signals : when signals do not have the same frequency ( ω ) solve the circuit separately for each different frequency ( ω ) – then add the individual results R 2 + i 1 (t) v s (t) R 1 – Discussion #13 – Phasors ECEN 301 17

Phasors of Different Frequencies  Example2 : compute the resistor voltages  i s (t) = 0.5cos[2 π (100t)] A  v s (t) = 20cos[2 π (1000t)] V  R 1 = 150 Ω , R2 = 50 Ω + R 2 – + + i 1 (t) v s (t) R 1 – – Discussion #13 – Phasors ECEN 301 18

Phasors of Different Frequencies  Example2 : compute the resistor voltages  i s (t) = 0.5cos[2 π (100t)] A  v s (t) = 20cos[2 π (1000t)] V  R 1 = 150 Ω , R2 = 50 Ω 1. Since the sources have different frequencies ( ω 1 = 2 π *100) and ( ω 2 = 2 π *1000) use superposition • first consider the ( ω 1 = 2 π *100) part of + R 2 – the circuit • When v s (t) = 0 – short circuit + i 1 (t) R 1 – Discussion #13 – Phasors ECEN 301 19

Phasors of Different Frequencies  Example2 : compute the resistor voltages  i s (t) = 0.5cos[2 π (100t)] A  v s (t) = 20cos[2 π (1000t)] V 1. Since the sources have different frequencies  R 1 = 150 Ω , R 2 = 50 Ω ( ω 1 = 2 π *100) and ( ω 2 = 2 π *1000) use superposition • first consider the ( ω 1 = 2 π *100) part of the circuit    ( ) 0 . 5 0 I j s +      i 1 (t) ( ) ( ) || V j V j I R R R 1 || R 2 1 2 2 I I 1 s – R R   1 2 I  s R R 1 2 ( 50 )( 150 )    0 . 5 0  ( 50 ) ( 150 )   18 . 75 0 Discussion #13 – Phasors ECEN 301 20