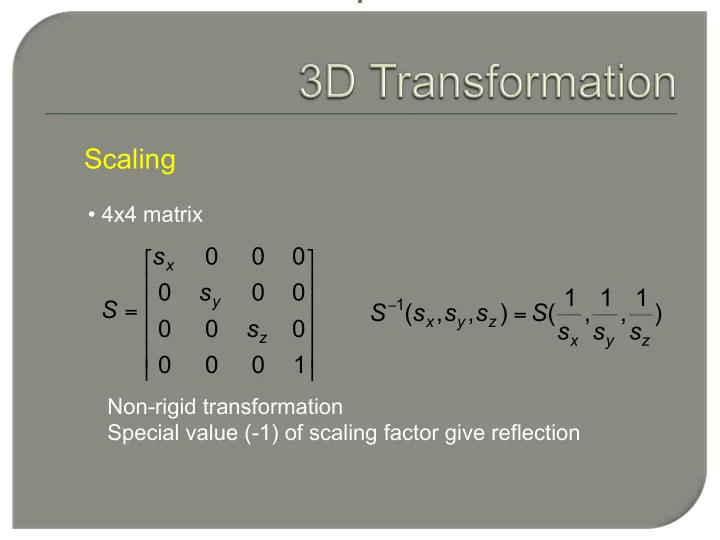
Scaling 4x4 matrix s 0 0 0 x 0 s 0 0 1 1 1 y 1 - PowerPoint PPT Presentation

Scaling • 4x4 matrix s 0 0 0 ⎡ ⎤ x ⎢ ⎥ 0 s 0 0 1 1 1 y 1 S ⎢ ⎥ S − ( s , s , s ) S ( , , ) = = x y z 0 0 s 0 s s s ⎢ ⎥ z x y z ⎢ ⎥ 0 0 0 1 ⎣ ⎦ Non-rigid transformation Special value (-1) of scaling factor give reflection

Rotation • About X-axis Y 1 0 0 0 ⎡ ⎤ ⎢ ⎥ 0 cos θ sin θ 0 R x ⎢ ⎥ = 0 sin θ cos θ 0 − ⎢ ⎥ X ⎢ ⎥ 0 0 0 1 ⎣ ⎦ Z

Rotation • About Z-axis Y cos ψ sin ψ 0 0 ⎡ ⎤ ⎢ ⎥ sin ψ cos ψ 0 0 − R z ⎢ ⎥ = 0 0 1 0 ⎢ ⎥ X ⎢ ⎥ 0 0 0 1 ⎣ ⎦ Z

Rotation • About Y-axis Y cos φ 0 sin φ 0 − ⎡ ⎤ ⎢ ⎥ 0 1 0 0 R y ⎢ ⎥ = sin φ 0 cos φ 0 ⎢ ⎥ X ⎢ ⎥ 0 0 0 1 ⎣ ⎦ Z

Rotations Rigid Transformation 1 R − ( θ ) R ( θ ) = − 1 T − R ( θ ) R ( θ ) = Orthogonal Matrix

Translation 1 0 0 0 ⎡ ⎤ ⎢ ⎥ 0 1 0 0 T ⎢ ⎥ = 0 0 1 0 ⎢ ⎥ ⎢ ⎥ l m n 1 ⎣ ⎦ Rigid transformation 1 T − ( l , m , n ) T ( l , m , n ) = − − −

Shear Off diagonal elements 1 b c 0 ⎡ ⎤ ⎢ ⎥ d 1 f 0 S ⎢ ⎥ = g h 1 0 ⎢ ⎥ ⎢ ⎥ 0 0 0 1 ⎣ ⎦ Non-rigid transformation

Shear Y (x, y) (x ’ , y ’ ) θ 1 0 0 0 X ⎡ ⎤ ⎢ ⎥ cot 1 0 0 θ x ' x y cot θ = + H ( ) ⎢ ⎥ θ = yz 0 0 1 0 y ' y = ⎢ ⎥ ⎢ ⎥ z ' z 0 0 0 1 = ⎣ ⎦ 1 − H ( θ ) H ( θ ) = − yz yz

Concatenation of Transformations Transformations: T 1 , T 2 , T 3 X ' ((( XT ) T ) T ) XT T T = = 1 2 3 1 2 3 T 1 T 2 T 3 X X ’ Alternatively, T 1 T 2 T 3 T T T T = 1 2 3 T X ' XT = X X ’ Pipeline unit

Rotation about a fixed point Rotation of a cube about its center (about Z-axis) Y C X X ' XT ( C ) R ( θ ) T ( C ) = − Z

Rotation about an arbitrary axis Axis: P 0 (x 0 , y 0 , z 0 ), (C x , C y , C z ) Angle: δ Y P C y X O C z C x OP: Unit vector Z O: (x 0 , y 0 , z 0 ) Translation (-x 0 , -y 0 , -z 0 )

Rotation about an arbitrary axis Axis: P 0 (x 0 , y 0 , z 0 ), (C x , C y , C z ) Angle: δ Y d P Rotation about X axis by α C y C α z cos α = X d O C z C y sin α C x = d Z

Rotation about an arbitrary axis Axis: P 0 (x 0 , y 0 , z 0 ), (C x , C y , C z ) Angle: δ Y Rotation about X axis by α O cos β d = X β 1 d sin β C d = x C x Z

Rotation about an arbitrary axis Complete Transformation M T ( P ) R ( α ) R ( β ) R ( δ ) R ( β ) R ( α ) T ( P ) = − − − 0 x y z y x 0

General a b c p ⎡ ⎤ ⎢ ⎥ d e f q S ⎢ ⎥ = g h i r ⎢ ⎥ ⎢ ⎥ l m n s ⎣ ⎦

Projections A Projectors A ’ B B ’ Center of Projection Plane Projection Perspective

Projections A Projectors A ’ B B ’ Projection Plane At Infinity Parallel

Parallel Projections Orthographic Top View Y X Z Side View Front View

Parallel Projections Orthographic • Multiviews (x=0 or y=0 or z=0 planes), one View is not adequate • True size and shape for lines On z=0 plane 1 0 0 0 ⎡ ⎤ ⎢ ⎥ 0 1 0 0 P ⎢ ⎥ = 0 0 0 0 ⎢ ⎥ ⎢ ⎥ 0 0 0 1 ⎣ ⎦

Parallel Projections Orthographic

Parallel Projections Axonometric • Additional rotation,translation and then projection on z=0 plane * * 1 0 0 1 x y 0 1 ⎡ ⎤ ⎡ ⎤ x x ⎢ ⎥ ⎢ ⎥ * * [ ][ ] [ ] U T 0 1 0 1 T x y 0 1 = = y y ⎢ ⎥ ⎢ ⎥ * * 0 0 1 1 x y 0 1 ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ z z ⎣ ⎦ * 2 * 2 * 2 * 2 * 2 * 2 f x y ; f x y ; f x y = + = + = + x x x y y y z z z

Parallel Projections Axonometric Three types • Trimetric: No foreshortening is the same. • Dimetric: Two foreshortenings are the same. • Isometric: All foreshortenings are the same.

Parallel Projections Axonometric Trimetric Dimetric Isometric f f f f f f f f = ≠ ≠ = = y z x y z x y z

Parallel Projections Isometric Let there be 2 rotations a) about y-axis φ b) about x-axis θ cos φ 0 sin φ 0 1 0 0 0 1 0 0 0 − ⎡ ⎤ ⎡ ⎤ ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ 0 1 0 0 0 cos θ sin θ 0 0 1 0 0 T ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ = sin φ 0 cos φ 0 0 sin θ cos θ 0 0 0 0 0 − ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ 0 0 0 1 0 0 0 1 0 0 0 1 ⎣ ⎦ ⎣ ⎦ ⎣ ⎦

Parallel Projections Isometric Let there be 2 rotations a) about y-axis φ b) about x-axis θ cos φ sin φ sin θ 0 0 ⎡ ⎤ ⎢ ⎥ 0 cos θ 0 0 T ⎢ ⎥ = sin φ cos φ sin θ 0 0 − ⎢ ⎥ ⎢ ⎥ 0 0 0 1 ⎣ ⎦

Parallel Projections Isometric cos φ sin φ sin θ 0 0 ⎡ ⎤ 1 0 0 1 ⎡ ⎤ ⎢ ⎥ 0 cos θ 0 0 ⎢ ⎥ [ ][ ] U T 0 1 0 1 ⎢ ⎥ = ⎢ ⎥ sin φ cos φ sin θ 0 0 ⎢ − ⎥ 0 0 1 1 ⎢ ⎥ ⎣ ⎦ ⎢ ⎥ 0 0 0 1 ⎣ ⎦ cos φ sin φ sin θ 0 1 ⎡ ⎤ ⎢ ⎥ 0 cos θ 0 1 = ⎢ ⎥ sin φ cos φ sin θ 0 1 ⎢ − ⎥ ⎣ ⎦

Parallel Projections Isometric 2 * 2 * 2 2 2 2 f x y cos φ sin φ sin θ = + = + x x x 2 * 2 * 2 2 f x y cos θ = + = y y y 2 * 2 * 2 2 2 2 f x y sin φ cos φ sin θ = + = + z z z

Parallel Projections Isometric f f f f = = = x y z 2 2 2 2 f f cos φ sin φ sin θ cos θ = ⇒ + = x y 2 2 2 2 f f sin φ cos φ sin θ cos θ = ⇒ + = y z Solving equations find θ , φ and f

Parallel Projections Oblique • Non-perpendicular projectors to the plane of projection • True shape and size for the faces parallel to the projection plane is preserved

Parallel Projections Oblique

Parallel Projections Oblique x p = x + L cos φ y y p = y + L sin φ P ’’ (x p ,y p ) P(x,y,z) tan α =z/L or L = z cot α α L φ x z P ’ (x,y)

Parallel Projections Oblique When α =45 o => Cavalier Lines perpendicular to the y projection plane are not foreshortened P ’’ (x p ,y p ) P(x,y,z) α When cot α = ½ => Cabinet L φ Lines perpendicular to the x z projection plane are P ’ (x,y) foreshortened by half φ is typically 30 0 or 45 0

Perspective Projections A Projectors • Parallel lines converge • Non-uniform A ’ foreshortening • Helps in depth B perception, important B ’ for 3D viewing Center of • Shape is not preserved Projection Plane Projection

Perspective Projections

Perspective Projections Matrix Form 1 0 0 0 ⎡ ⎤ ⎢ ⎥ 0 1 0 0 [ x y z 1 ] [ x y z rz 1 ] ⎢ ⎥ = + 0 0 1 r ⎢ ⎥ ⎢ ⎥ 0 0 0 1 ⎣ ⎦ x y z [ ] ⎡ ⎤ * * * x y z 1 1 = ⎢ ⎥ rz 1 rz 1 rz 1 + + + ⎣ ⎦

Perspective Projections Matrix Form Projection on z=0 plane 1 0 0 0 1 0 0 0 ⎡ ⎤ ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ 0 1 0 0 0 1 0 0 T P [ ][ P P ] ⎢ ⎥ ⎢ ⎥ = = = rz r z 0 0 1 r 0 0 0 0 ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ 0 0 0 1 0 0 0 1 ⎣ ⎦ ⎣ ⎦ x y [ ] ⎡ ⎤ * * * x y z 1 0 1 = ⎢ ⎥ rz 1 rz 1 + + ⎣ ⎦

Perspective Projections Geometrically Y y * y l 1 P*(x*,y*) l 2 * y y z l c 2 , = = l l l z z l l P(x,y,z) − − − X 2 2 1 c 2 1 z c y * y ⇒ = z 1 Z − z c

Perspective Projections Geometrically z c Y l 1 x P*(x*,y*) x * l 2 * x x x * x P(x,y,z) = ⇒ = X z z z z − z c 1 c c − z c When r = - 1/ z c this becomes same Z as obtained in matrix form

Perspective Projections Vanishing Point Set of parallel lines not parallel to the projection plane converge to Vanishing Point VP z Y X Z

Perspective Projections Vanishing Point Point at infinity on +Z axis : (homogenous) [ ] 0 0 1 0 1 0 0 0 ⎡ ⎤ ⎢ ⎥ 0 1 0 0 [ ] ' ' ' x y z w [ 0 0 1 0 ] ⎢ ⎥ = 0 0 1 r ⎢ ⎥ ⎢ ⎥ 0 0 0 1 ⎣ ⎦ [ 0 0 1 r ] = ] [ ] [ 1 * * * x y z 1 0 0 1 = r Recall r = -1/z c , the vanishing point is at -z c

Perspective Projections Single Point Perspective COP on X-axis 1 0 0 p ⎡ ⎤ ⎢ ⎥ 0 1 0 0 [ ] [ ] x y z 1 x y z px 1 ⎢ ⎥ = + 0 0 1 0 ⎢ ⎥ ⎢ ⎥ 0 0 0 1 ⎣ ⎦ x y z ⎡ ⎤ [ ] * * * x y z 1 1 = ⎢ ⎥ px 1 px 1 px 1 + + + ⎣ ⎦ COP (-1/p 0 0 1) VP x (1/p 0 0 1)

Perspective Projections Single Point Perspective COP on Y-axis 1 0 0 0 ⎡ ⎤ ⎢ ⎥ 0 1 0 q [ ] [ ] x y z 1 x y z qy 1 ⎢ ⎥ = + 0 0 1 0 ⎢ ⎥ ⎢ ⎥ 0 0 0 1 ⎣ ⎦ x y z ⎡ ⎤ [ ] * * * x y z 1 1 = ⎢ ⎥ qy 1 qy 1 qy 1 + + + ⎣ ⎦ COP (0 -1/q 0 1) VP x (0 1/q 0 1)