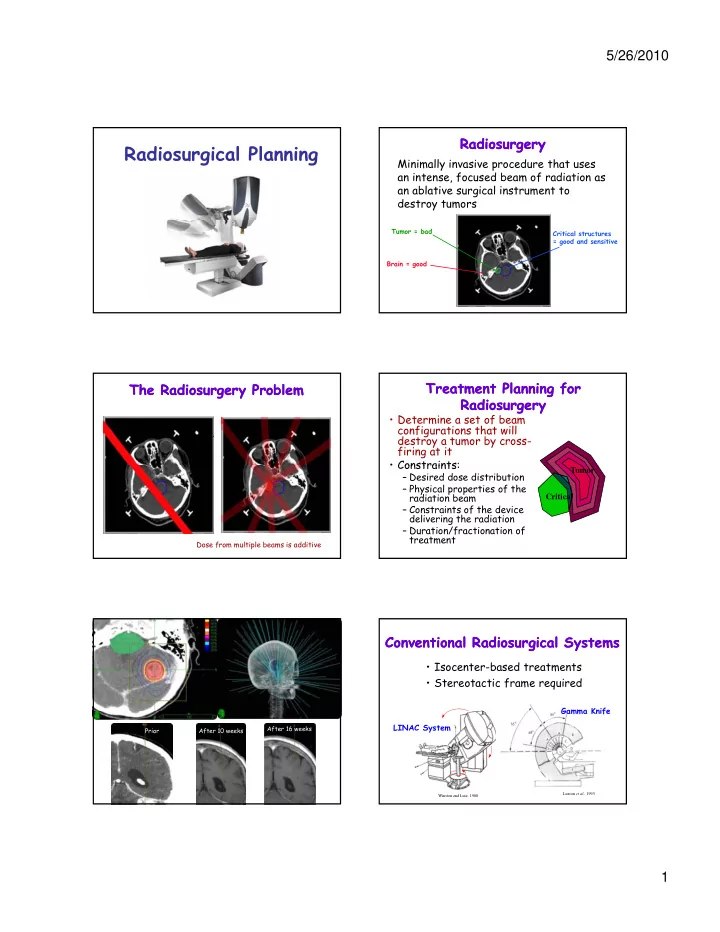

5/26/2010 Radiosurgery Radiosurgery Radiosurgical Planning Minimally invasive procedure that uses an intense, focused beam of radiation as an ablative surgical instrument to destroy tumors Tumor = bad Critical structures = good and sensitive Brain = good Treatment Planning for Treatment Planning for The Radiosurgery Problem The Radiosurgery Problem Radiosurgery Radiosurgery • Determine a set of beam configurations that will destroy a tumor by cross- firing at it • Constraints: Constraints: Tumor – Desired dose distribution – Physical properties of the radiation beam Critical – Constraints of the device delivering the radiation – Duration/fractionation of treatment Dose from multiple beams is additive Conventional Radiosurgical Systems Conventional Radiosurgical Systems • Isocenter-based treatments • Stereotactic frame required Gamma Knife Gamma Knife LINAC System After 16 weeks Prior After 10 weeks Luxton et al. , 1993 Winston and Lutz, 1988 1
5/26/2010 Stereotactic Frame for Stereotactic Frame for Isocenter- Isocenter -Based Treatments Based Treatments Localization Localization • All beams converge at the isocenter • The resulting region of high dose is • Painful spherical • Fractionation of treatments is Nonspherically shaped tumors are difficult approximated by multiple spheres • Treatment of – “Cold Spots” where coverage is poor extracranial tumors – “Hot Spots” where the spheres overlap is impossible – Over-irradiation of healthy tissue The CyberKnife The CyberKnife CyberKnife (Accuray) CyberKnife (Accuray) linear accelerator robotic gantry X-Ray cameras http://accuray.com/ Treatment Planning Treatment Planning Inputs to CARABEAMER Inputs to CARABEAMER Becomes More Difficult Becomes More Difficult (1) Regions of Interest: • Much larger solution space – Beam configuration space has greater dimensionality – Number of beams can be much larger – Number of beams can be much larger – More complex interactions between beams • Path planning – Avoid collisions – Do not obstruct X-ray cameras � Automatic planning required (CARABEAMER) Surgeon delineates the CARABEAMER creates regions of interest 3D regions 2
5/26/2010 Basic Problem Solved by Basic Problem Solved by Inputs to CARABEAMER Inputs to CARABEAMER CARABEAMER CARABEAMER (2) Dose Constraints: • Given: Dose to tumor – Spatial arrangement of regions of interest – Dose constraints for each region: a ≤ D ≤ b Falloff of dose Tumor around tumor around tumor – Max number of beams allowed: N (~100-400) Dose to critical Critical • Find: structure Falloff of dose in critical structure – N beam configurations (or less) that generate dose distribution that meets the constraints. (3) Maximum number of beams Beam Configuration Beam Configuration CARABEAMER’s Approach CARABEAMER’s Approach • Position and orientation of the radiation 1. Initial Sampling: Generate many (> N) beams at random, with each beam beam z having a reasonable probability of being part of the solution. 2. Weighting: φ Use linear programming to test whether the beams can y produce a dose distribution that satisfies the input produce a dose distribution that satisfies the input (x, y) constraints. 3. Iterative Re-Sampling: x θ Eliminate beams with small weights and re-sample more beams around promising beams. • Amount of radiation or beam weight 4. Iterative Beam Reduction: • Collimator diameter Progressively reduce the number of beams in the solution. � Find 6N parameters that satisfy the constraints Deterministic Beam Selection is Deterministic Beam Selection is Initial Beam Sampling Initial Beam Sampling Less Robust Less Robust • Generate even distribution of target points on the surface of the tumor • Define beams at random orientations through these points 3
5/26/2010 Dose Distribution Before Beam Curvature Bias Curvature Bias Weighting • Place more target points in regions of high curvature 50% Isodose Surface 80% Isodose Surface CARABEAMER’s Approach CARABEAMER’s Approach Beam Weighting Beam Weighting 1. Initial Sampling: Generate many (> N) beams at random, with each beam • Construct geometric arrangement of regions formed having a reasonable probability of being part of the by the beams and the tissue structures solution. 2. Weighting: Use linear programming to test whether the beams can • Assign constraints to produce a dose distribution that satisfies the input produce a dose distribution that satisfies the input each cell of the h ll f h constraints. arrangement: T B1 3. Iterative Re-Sampling: – Tumor constraints Eliminate beams with small weights and re-sample more beams around promising beams. – Critical C B2 4. Iterative Beam Reduction: constraints Progressively reduce the number of beams in the B4 solution. B3 Results of Beam Weighting Results of Beam Weighting Linear Programming Problem Linear Programming Problem Before Weighting After Weighting • 2000 ≤ Tumor ≤ 2200 50% 2000 ≤ B2 + B4 ≤ 2200 2000 ≤ B4 ≤ 2200 Isodose 2000 ≤ B3 + B4 ≤ 2200 surfaces 2000 ≤ B3 ≤ 2200 T T B1 2000 ≤ B1 + B3 + B4 ≤ 2200 2000 ≤ B1 + B4 ≤ 2200 2000 ≤ B1 + B4 ≤ 2200 2000 ≤ B1 + B2 + B4 ≤ 2200 2000 ≤ B1 ≤ 2200 2000 ≤ B1 + B2 ≤ 2200 C B2 • 0 ≤ Critical ≤ 500 0 ≤ B2 ≤ 500 80% B4 Isodose surfaces B3 4
5/26/2010 CARABEAMER’s Approach CARABEAMER’s Approach CARABEAMER’s Approach CARABEAMER’s Approach 1. Initial Sampling: 1. Initial Sampling: Generate many (> N) beams at random, with each beam Generate many (> N) beams at random, with each beam having a reasonable probability of being part of the having a reasonable probability of being part of the solution. solution. 2. Weighting: 2. Weighting: Use linear programming to test whether the beams can Use linear programming to test whether the beams can produce a dose distribution that satisfies the input produce a dose distribution that satisfies the input produce a dose distribution that satisfies the input produce a dose distribution that satisfies the input constraints. constraints. 3. Iterative Re-Sampling: 3. Iterative Re-Sampling: Eliminate beams with small weights and re-sample more Eliminate beams with small weights and re-sample more beams around promising beams. beams around promising beams. 4. Iterative Beam Reduction: 4. Iterative Beam Reduction: Progressively reduce the number of beams in the Progressively reduce the number of beams in the solution. solution. Plan Review Plan Review Treatment Planning: Extensions � Simple path planning • Calculate resulting dose distribution and collision avoidance • Radiation oncologist reviews • If satisfactory, treatment can be y, delivered • If not... � Automatic collimator Tumor selection – Add new constraints Critical – Adjust existing constraints Another Sample Case Another Sample Case Evaluation on Sample Case 50% Isodose Surface 80% Isodose Linac plan CARABEAMER ’s plan Surface 80% Isodose surface 80% Isodose surface LINAC plan CARABEAMER’s plan 5
Recommend
More recommend