R EGRESSION RANK - SCORES TESTS IN R D EFINITION : R EGRESSION - PowerPoint PPT Presentation

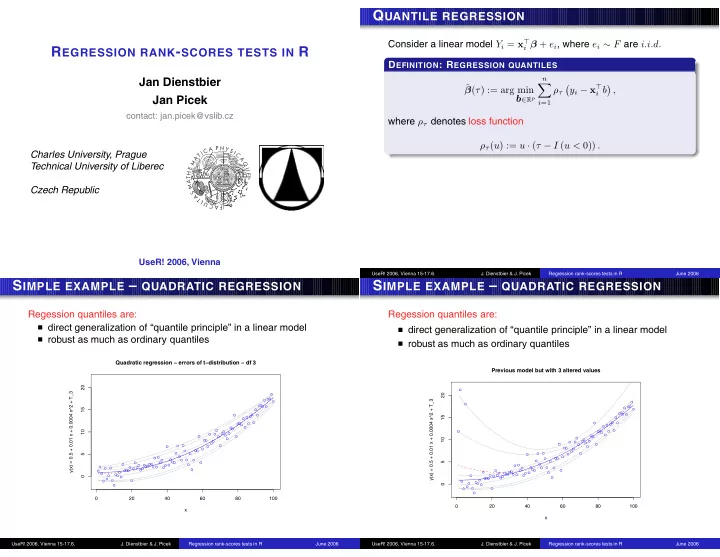
Q UANTILE REGRESSION Consider a linear model Y i = x ⊤ i β + e i , where e i ∼ F are i.i.d. R EGRESSION RANK - SCORES TESTS IN R D EFINITION : R EGRESSION QUANTILES Jan Dienstbier n ˆ � y i − x ⊤ � � β ( τ ) := arg min ρ τ i b , Jan Picek b ∈ R p i =1 contact: jan.picek@vslib.cz where ρ τ denotes loss function ρ τ ( u ) := u · ( τ − I ( u < 0)) . Charles University, Prague Technical University of Liberec Czech Republic UseR! 2006, Vienna UseR! 2006, Vienna 15-17.6. J. Dienstbier & J. Picek Regression rank-scores tests in R June 2006 S IMPLE EXAMPLE – QUADRATIC REGRESSION S IMPLE EXAMPLE – QUADRATIC REGRESSION Regession quantiles are: Regession quantiles are: � direct generalization of “quantile principle” in a linear model � direct generalization of “quantile principle” in a linear model � robust as much as ordinary quantiles � robust as much as ordinary quantiles Quadratic regression − errors of t − distribution − df 3 Previous model but with 3 altered values 20 y(x) = 0.5 + 0.01 x + 0.0004 x^2 + T_3 20 y(x) = 0.5 + 0.01 x + 0.0004 x^2 + T_3 15 15 10 10 5 5 0 0 0 20 40 60 80 100 0 20 40 60 80 100 x x UseR! 2006, Vienna 15-17.6. J. Dienstbier & J. Picek Regression rank-scores tests in R June 2006 UseR! 2006, Vienna 15-17.6. J. Dienstbier & J. Picek Regression rank-scores tests in R June 2006

R EGRESSION RANKS R EGRESSION RANK - SCORES TESTS - T HE M ECHANISM D EFINITION : R EGRESSION RANK SCORES 1 calculate regression rank scores ˆ a ( τ ) de fi ned above a ∈ R n y ⊤ a ˆ a ( τ ) = arg max 2 choose the proper score function ϕ – this determines the form of the test and should be done in respect to the used data in conditions that usual selections are eg. logistic (Wilcoxon), normal (van der Waerden) or sign scores X ⊤ a = (1 − τ ) X ⊤ 1 n , a ∈ [0 , 1] n . 3 calculate scores ˆ b ni , i = 1 , . . . , n � solution of the dual linear programming problem � 1 ˆ b ni = − ϕ ( u ) d ˆ a ni ( u ) , i = 1 , . . . , n � behave similary as ordinary ranks ⇒ regression rank tests 0 4 plug this to the statistic invariant to regression – e.g. n S n 0 ( Y ) = 1 Y i ˆ b ni = n − 1 Y ⊤ ˆ � b n n i =1 UseR! 2006, Vienna 15-17.6. J. Dienstbier & J. Picek Regression rank-scores tests in R June 2006 UseR! 2006, Vienna 15-17.6. J. Dienstbier & J. Picek Regression rank-scores tests in R June 2006 A N EXAMPLE - G OODNESS - OF - FIT TEST . . . IN R LANGUAGE IT MEANS . . . 1 useR! library quantreg , where are implemented basic methods E XAMPLE of quantile regressions (regression ranks included) In the linear model Y i = x ⊤ i β + σe i , where e i ∼ F is continuous distribution it holds under H 0 : F ( e ) ≡ F 0 ( e/σ ) � � S n 0 ( Y ) D n = n 1 / 2 T ∗ � 0 , ξ 2 ( F 0 ) � − → N log , β 1 (3 / 4) − ˆ ˆ β 1 (1 / 4) Common properties of such tests: 1 quite robust – they are not affected by a heavy tailed F 2 independent to regression parameters ( β , σ ) – they needn’t to be estimated UseR! 2006, Vienna 15-17.6. J. Dienstbier & J. Picek Regression rank-scores tests in R June 2006 UseR! 2006, Vienna 15-17.6. J. Dienstbier & J. Picek Regression rank-scores tests in R June 2006

. . . IN R LANGUAGE IT MEANS . . . . . . IN R LANGUAGE IT MEANS . . . 1 useR! library quantreg , where are implemented basic methods 1 useR! library quantreg , where are implemented basic methods of quantile regressions (regression ranks included) of quantile regressions (regression ranks included) 2 scores can be computed via ranks 2 scores can be computed via ranks e.g. ranks(rq(data ∼ covar, tau=-1, score="wilcoxon")) e.g. ranks(rq(data ∼ covar, tau=-1, score="wilcoxon")) 3 score function can be speci fi ed as a parametr of ranks e.g. ranks(v, score="wilcoxon", tau=0.5) UseR! 2006, Vienna 15-17.6. J. Dienstbier & J. Picek Regression rank-scores tests in R June 2006 UseR! 2006, Vienna 15-17.6. J. Dienstbier & J. Picek Regression rank-scores tests in R June 2006 . . . IN R LANGUAGE IT MEANS . . . . . . IN R LANGUAGE IT MEANS . . . 1 useR! library quantreg , where are implemented basic methods 1 useR! library quantreg , where are implemented basic methods of quantile regressions (regression ranks included) of quantile regressions (regression ranks included) 2 scores can be computed via ranks 2 scores can be computed via ranks e.g. ranks(rq(data ∼ covar, tau=-1, score="wilcoxon")) e.g. ranks(rq(data ∼ covar, tau=-1, score="wilcoxon")) 3 score function can be speci fi ed as a parametr of ranks 3 score function can be speci fi ed as a parametr of ranks e.g. ranks(v, score="wilcoxon", tau=0.5) e.g. ranks(v, score="wilcoxon", tau=0.5) 4 plug this to a suitable statistic and compare it with it’s proper 4 plug this to a suitable statistic and compare it with it’s proper asymptotical p -value asymptotical p -value eg. properly normalized T ∗ n compare with 1 - pnorm(0.95) . . . eg. properly normalized T ∗ n compare with 1 - pnorm(0.95) . . . As an example we implemented described GOF test. UseR! 2006, Vienna 15-17.6. J. Dienstbier & J. Picek Regression rank-scores tests in R June 2006 UseR! 2006, Vienna 15-17.6. J. Dienstbier & J. Picek Regression rank-scores tests in R June 2006

A UTOREGRESSION A UTOREGRESSION Regression rank scores concept can be generalized on AR time Regression rank scores concept can be generalized on AR time series series t = 0 , ± 1 , ± 2 . . . . t = 0 , ± 1 , ± 2 . . . . X t = θ 1 X t − 1 + . . . + θ p X t − p + ǫ t , X t = θ 1 X t − 1 + . . . + θ p X t − p + ǫ t , Autorergression rank scores tests proposed in literature Autorergression rank scores tests proposed in literature � independence of two AR time series � independence of two AR time series � hypothesis AR ( p − 1) against AR ( p ) � hypothesis AR ( p − 1) against AR ( p ) . . . other tests can be derived from quite general theory Hallin and . . . other tests can be derived from quite general theory Hallin and Jure ˇ cková (1997). Jure ˇ cková (1997). � we implemented these tests in R � basic procedures taken from quantreg � only minor changes needed UseR! 2006, Vienna 15-17.6. J. Dienstbier & J. Picek Regression rank-scores tests in R June 2006 UseR! 2006, Vienna 15-17.6. J. Dienstbier & J. Picek Regression rank-scores tests in R June 2006 P ROPOSALS – POSSIBLE IMPROVEMENTS OF Q UANTILE REGRESSION RANKS AND R IMPLEMENTATION OF REGRESSION RANK SCORES IN R � with quantreg package, there can be easily implemented various regression rank tests Althought there are excellent basic algoritms in quantreg the � procedures are universal enough to extend these concept even implementation of regression rank tests is still little bit a “stub”. on the AR series � surprisingly large scale of hypothesis - eg. GOF, AR We propose: independence � eliminate gaps in the implementation of the linear submodel hypothesis basic procedure rrs.test. doesn’t show p-values, user must know little bit more about the test to use it implementation of the test in anova.rq isn’t user-friendly, sometimes is hard to understand, what results user gets � more than three types of score functions – make it universally � direct treatment of autoregression series with quantreg UseR! 2006, Vienna 15-17.6. J. Dienstbier & J. Picek Regression rank-scores tests in R June 2006 UseR! 2006, Vienna 15-17.6. J. Dienstbier & J. Picek Regression rank-scores tests in R June 2006

Q UANTILE REGRESSION RANKS AND R � with quantreg package, there can be easily implemented various R EGRESSION RANK - SCORES TESTS IN R regression rank tests � procedures are universal enough to extend these concept even on the AR series Jan Dienstbier � surprisingly large scale of hypothesis - eg. GOF, AR Jan Picek independence contact: jan.picek@vslib.cz Authors hope, that thanks to R it will be possible to evaluate, Charles University, Prague whether these tests interesting from the theoretical point of view Technical University of Liberec can be used in the daily praxis. Czech Republic UseR! 2006, Vienna UseR! 2006, Vienna 15-17.6. J. Dienstbier & J. Picek Regression rank-scores tests in R June 2006 UseR! 2006, Vienna 15-17.6. J. Dienstbier & J. Picek Regression rank-scores tests in R June 2006