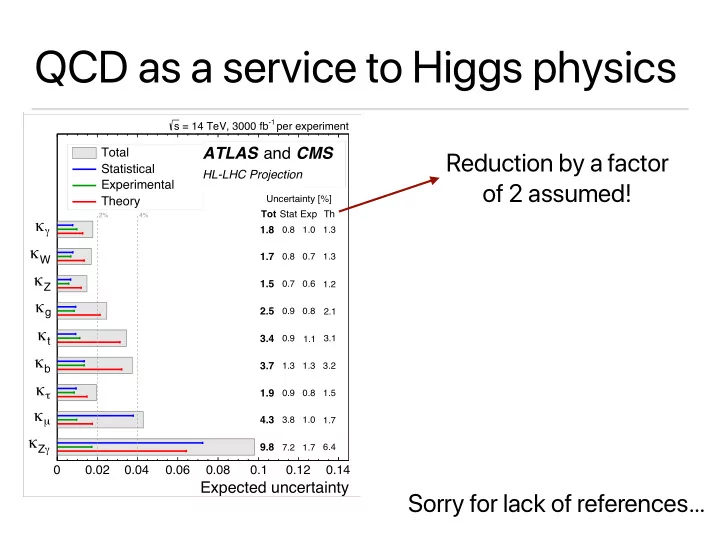
QCD as a service to Higgs physics -1 s = 14 TeV, 3000 fb per - PowerPoint PPT Presentation

QCD as a service to Higgs physics -1 s = 14 TeV, 3000 fb per experiment ATLAS and CMS Total Reduction by a factor Statistical HL-LHC Projection Experimental of 2 assumed! Uncertainty [%] Theory Tot Stat Exp Th 2% 4% κ 1.8 0.8 1.0 1.3 γ κ 1.7 0.8 0.7 1.3 W κ 1.5 0.7 0.6 1.2 Z κ g 2.5 0.9 0.8 2.1 κ 3.4 0.9 1.1 3.1 t κ 3.7 1.3 1.3 3.2 b κ 1.9 0.9 0.8 1.5 τ κ 4.3 3.8 1.0 1.7 µ κ 9.8 7.2 1.7 6.4 Z γ 0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 Expected relative uncertainty Expected uncertainty Sorry for lack of references…

ATLAS 3000 fb − 1 uncertainty [%] CMS 3000 fb − 1 uncertainty [%] Total Stat SigTh BkgTh Exp S1 3.7 0.9 2.2 1.4 2.5 Total Stat SigTh BkgTh Exp κ γ S2 2.4 0.9 1.1 0.9 1.7 S1 2.9 1.1 1.8 1.0 1.7 κ γ S2 2.0 1.1 0.9 0.8 1.2 S1 3.1 0.8 1.9 1.9 1.3 κ W S2 2.2 0.8 1.2 1.3 1.2 S1 2.6 1.0 1.7 1.1 1.1 κ W S2 1.8 1.0 0.9 0.8 0.8 S1 2.6 0.8 1.8 1.2 1.1 κ Z S2 1.8 0.8 1.0 0.8 0.9 S1 2.4 1.0 1.7 0.9 0.9 κ Z S2 1.7 1.0 0.9 0.7 0.7 S1 4.2 1.0 3.2 2.2 1.4 κ g S2 3.1 1.0 2.2 1.6 1.2 S1 4.0 1.1 3.4 1.3 1.2 κ g S2 2.5 1.1 1.7 1.1 1.0 S1 6.3 1.1 4.9 3.4 1.6 κ t S2 4.2 1.1 2.6 2.7 1.4 S1 5.5 1.0 4.4 2.7 1.6 κ t S2 3.5 1.0 2.2 2.1 1.2 S1 6.2 1.6 3.7 4.1 2.3 κ b S2 4.4 1.6 2.1 2.8 2.0 S1 6.0 2.0 4.3 2.9 2.3 κ b S2 4.0 2.0 2.0 2.2 1.8 S1 3.7 1.1 2.6 1.8 1.7 κ τ S2 2.7 1.1 1.5 1.2 1.6 S1 2.8 1.2 1.8 1.1 1.4 κ τ S2 2.0 1.2 1.0 0.9 1.0 S1 7.7 6.4 3.6 1.4 1.9 κ µ S2 7.0 6.4 2.0 0.9 1.8 S1 6.7 4.7 2.5 1.0 3.9 κ µ S2 5.0 4.7 1.3 0.8 1.1 S1 12.7 10.2 6.9 1.4 2.5 κ Z γ S2 12.4 10.2 6.4 0.9 2.4

ATLAS CMS 3000 fb − 1 uncertainty [%] 3000 fb − 1 uncertainty [%] Total Stat Exp SigTh BkgTh Total Stat Exp SigTh BkgTh S1 3.5 0.8 2.1 2.1 1.6 S1 2.4 0.8 1.2 1.6 0.9 σ ggH σ ggH S2 2.4 0.8 1.7 1.2 1.0 S2 1.7 0.8 0.9 0.9 0.6 S1 5.5 2.0 2.7 3.7 2.1 S1 4.1 2.6 2.1 2.0 1.3 σ VBF σ VBF S2 4.2 2.0 2.3 2.2 1.7 S2 3.5 2.6 1.6 1.8 0.3 S1 9.3 4.0 4.0 5.1 5.4 S1 8.1 4.6 5.2 2.6 3.3 σ WH σ WH S2 7.7 4.0 3.4 3.3 4.5 S2 6.4 4.6 3.2 1.5 2.7 S1 6.2 3.4 2.4 3.4 3.0 S1 6.7 3.9 2.1 4.3 2.5 σ ZH σ ZH S2 4.8 3.4 1.8 2.0 2.1 S2 5.4 3.9 1.7 2.4 2.3 S1 6.7 1.9 3.1 3.7 4.3 S1 5.8 1.8 3.1 1.9 4.1 σ ttH σ ttH S2 5.3 1.9 2.8 2.4 3.3 S2 4.6 1.8 2.4 1.1 3.4

ATLAS 3000 fb − 1 relative uncertainty [%] CMS 3000 fb − 1 relative uncertainty [%] Total Stat Exp SigTh BkgTh S1 6.0 1.2 4.7 3.3 1.4 Total Stat Exp SigTh BkgTh B γγ S2 3.7 1.2 2.9 1.8 0.6 S1 4.4 1.3 2.6 3.3 0.3 B γγ S2 3.0 1.3 1.7 1.9 0.3 S1 5.8 1.0 2.8 4.3 2.6 B WW S2 4.4 1.0 2.4 3.2 1.6 S1 4.0 1.0 1.4 3.5 1.0 B WW S2 2.8 1.0 1.1 2.2 0.9 S1 5.3 1.6 3.0 3.7 1.7 B ZZ S2 3.8 1.6 2.7 1.9 1.0 S1 5.0 1.6 2.5 3.5 1.9 B ZZ S2 3.2 1.6 1.7 2.1 0.7 S1 7.6 2.0 2.4 5.0 4.7 B bb S2 5.0 2.0 1.9 2.8 3.2 S1 7.0 2.1 2.3 5.2 3.6 B bb S2 4.7 2.1 1.7 2.4 2.9 S1 6.0 1.7 2.7 4.4 2.4 B ττ S2 4.4 1.7 2.5 2.8 1.7 S1 3.9 1.6 1.9 2.6 1.5 B ττ S2 2.9 1.6 1.4 1.9 0.6 S1 14.9 12.7 3.2 6.8 0.3 B µµ S2 13.7 12.7 3.2 3.7 0.3 S1 12.8 9.1 7.6 4.7 0.8 B µµ S2 9.6 9.1 1.7 2.6 0.8 S1 24.2 20.3 4.5 12.2 0.0 B Z γ S2 24.2 20.3 4.5 12.2 0.0

gg → H 12 10 � i / � total × 100 % 8 � ( PDF + � s ) 6 � ( 1 / m t ) � ( t,b,c ) � ( EW ) 4 � ( PDF - TH ) 2 � ( scale ) 0 0 20 40 60 80 100 Collider Energy / TeV

pp → ZH Important for HZZ and Hbb couplings Table 10: Cross-section for the process pp → ZH . The predictions for the gg → ZH channel are computed at LO, rescaled by the NLO K -factor in the m t → ∞ limit, and supplemented by the NLL soft resummation. The photon contribution is omitted. Results are given for a Higgs boson mass m H = 125 . 09 GeV. √ s [TeV ] ∆ scale [%] ∆ PDF ⊕ α s [%] σ NNLO QCD ⊗ NLO EW [pb] +3 . 50 0 . 880 1 . 65 13 − 2 . 68 +3 . 61 14 0 . 981 1 . 90 − 2 . 94 +5 . 42 27 2 . 463 2 . 24 − 4 . 00 Dominant uncertainty from gg → ZH

gg → ZH Loop induced NLO difficult! (a) (b) (c) (d) (e) (f) (g) Determining arbitrary Feynman integrals by vacuum integrals Xiao Liu 1, ∗ and Yan-Qing Ma 1, 2, 3, † Might be possible Towards a new approximation for pair-production and with new methods? associated-production of the Higgs boson Xiaofeng Xu a , Li Lin Yang a,b,c

H → bb Uncertainty for Higgs width and Hbb coupling G A G B G C G D Mixed QCD-EW ongoing Two-loop EW?

pp → ttH (signal) Table 15: NLO QCD+EW cross sections for t ¯ tH production at the 13 TeV LHC, taken from Ref. [45]. σ NLO m H [GeV ] QCD+EW [fb] Scale [%] α s [%] PDF [%] PDF+ α s [%] +5 . 8 124 . 59 512 . 2 2 . 0 3 . 0 3 . 6 − 9 . 2 +5 . 8 125 . 09 506 . 5 2 . 0 3 . 0 3 . 6 − 9 . 2 +5 . 8 125 . 59 500 . 7 2 . 0 3 . 0 3 . 6 − 9 . 2 Missing higher orders dominate

pp → ttH (signal) Table 15: NLO QCD+EW cross sections for t ¯ tH production at the 13 TeV LHC, taken from Ref. [45]. σ NLO m H [GeV ] QCD+EW [fb] Scale [%] α s [%] PDF [%] PDF+ α s [%] +5 . 8 124 . 59 512 . 2 2 . 0 3 . 0 3 . 6 − 9 . 2 +5 . 8 125 . 09 506 . 5 2 . 0 3 . 0 3 . 6 − 9 . 2 +5 . 8 125 . 59 500 . 7 2 . 0 3 . 0 3 . 6 − 9 . 2 Missing higher orders dominate NNLL resummation for the associated production of a top pair and a Higgs boson at 600 the LHC LHC 13 TeV 550 Alessandro Broggio, a, Andrea Ferroglia, b,c Ben D. Pecjak, d and Li Lin Yang e,f,g 500 σ [ pb ] NLO+NNLL known, but more 450 analysis necessary (scale choice, 400 higher order resummation, etc.) μ f ,0 = M μ f ,0 = M 2 350 NLO NLL NNLL nNLO NLO NLL NNLL nNLO

pp → ttH (signal) Table 15: NLO QCD+EW cross sections for t ¯ tH production at the 13 TeV LHC, taken from Ref. [45]. σ NLO m H [GeV ] QCD+EW [fb] Scale [%] α s [%] PDF [%] PDF+ α s [%] +5 . 8 124 . 59 512 . 2 2 . 0 3 . 0 3 . 6 − 9 . 2 +5 . 8 125 . 09 506 . 5 2 . 0 3 . 0 3 . 6 − 9 . 2 +5 . 8 125 . 59 500 . 7 2 . 0 3 . 0 3 . 6 − 9 . 2 Missing higher orders dominate NNLL resummation for the associated production of a top pair and a Higgs boson at 600 the LHC LHC 13 TeV 550 Alessandro Broggio, a, Andrea Ferroglia, b,c Ben D. Pecjak, d and Li Lin Yang e,f,g 500 σ [ pb ] NLO+NNLL known, but more 450 analysis necessary (scale choice, 400 higher order resummation, etc.) μ f ,0 = M μ f ,0 = M 2 350 NLO NLL NNLL nNLO NLO NLL NNLL nNLO NNLO highly wanted!

pp → ttH (background) tH ( b ¯ Theory progress on t ¯ b ) background Stefano Pozzorini b ¯ b t Stefan Pozzorini @ TOP2018 ¯ t tH ( b ¯ Dominant t ¯ tH theory systematics from t ¯ t + b -jet background to t ¯ b ) Only NLO is known at the moment! Resummation? NNLO? Clever scale choice to minimize higher orders?

pp → ttH (background) tW ± production Renormalization group improved predictions for t ¯ at hadron colliders Hai Tao Li, 1 Chong Sheng Li, 1, 2, ∗ and Shi Ang Li 1 Associated production of a top pair and a W boson at next-to-next-to-leading logarithmic accuracy. Alessandro Broggio, a Andrea Ferroglia, b,c Giovanni Ossola, b,c and Ben D. Pecjak d

<latexit sha1_base64="r3P4K6IpGR39txsuEkzvLadLo8E=">ACPXicbVDLSgMxFM3UV62vqks3wSK0mzLTCrSoht3VrAP6Is7adqGZjJDkhHK0M/xO/wAt7rwA8SNuHVr2s7CPi6EHM45l3vcQPOlLbtDyuxtr6xuZXcTu3s7u0fpA+PqsoPJaEV4nNf1l1QlDNBK5pTuBpOC5nNbc4e1Erz1RqZgvHvUoC0P+oL1GAFtqE76umBHhDg0f042wQeDKCjZn+7mMNXeJXeLsSOQq6Tzth5e1p4GTgxyKC4yp30V7Prk9CjQhMOSjUcO9CtCKRmhNxqhkqGgAZQp82DBTgUdWKpoeO8ZlhurjnS/OExlP2f0cEnlIjzXOydpqUZuQq7RGqHuXrYiJINRUkNmgXsix9vEkNdxlkhLNRwYAkczsiskAJBtsp2bMqBKJhWY5OMs5jDMqgW8k4xX3g4z5Ru4oyS6ASdoixy0AUqoTtURhVE0DN6RW/o3XqxPq1v62dmTVhxzGaK+v3D0mOr3c=</latexit> pp → ttH (background) tW ± production Renormalization group improved predictions for t ¯ at hadron colliders Hai Tao Li, 1 Chong Sheng Li, 1, 2, ∗ and Shi Ang Li 1 Associated production of a top pair and a W boson at next-to-next-to-leading logarithmic tW ± and t ¯ Large NLO corrections in t ¯ tt ¯ t accuracy. hadroproduction from supposedly subleading EW contributions Alessandro Broggio, a Andrea Ferroglia, b,c Giovanni Ossola, b,c and Ben D. Pecjak d Rikkert Frederix, a Davide Pagani, a and Marco Zaro b,c,d a Technische Universität München, James-Franck-Str. 1, D-85748 Garching, Germany b Nikhef, Science Park 105, NL-1098 XG Amsterdam, The Netherlands c Sorbonne Universités, UPMC Univ. Paris 06, UMR 7589, LPTHE, F-75005, Paris, France d CNRS, UMR 7589, LPTHE, F-75005, Paris, France tW ± and t ¯ Abstract: We calculate the complete-NLO predictions for t ¯ tt ¯ t production in proton–proton collisions at 13 and 100 TeV. All the non-vanishing contributions of O ( α i s α j ) O ( α s α 3 ) > O ( α 2 s α 2 ) tW ± and i + j = 4 , 5 for t ¯ with i + j = 3 , 4 for t ¯ tt ¯ t are evaluated without any approximation. tW ± we find that, due to the presence of tW → tW scattering, at 13(100) TeV the For t ¯ O ( α s α 3 ) contribution is about 12(70)% of the LO, i.e. , it is larger than the so-called NLO s α 2 ) terms) and has opposite sign. In the case of t ¯ tt ¯ EW corrections (the O ( α 2 t production, large contributions from electroweak scattering are already present at LO in the