< Q > < < < > > > H A 0 if P(x) does - PowerPoint PPT Presentation
CSE 311: Foundations of Computing announcements Fall 2013 Hand in Homework 9 now Lecture 29: Wrap up Pick up all old homework and exams now Review session Sunday, 3pm, EEB 125 List of Final Exam Topics and sampling of some
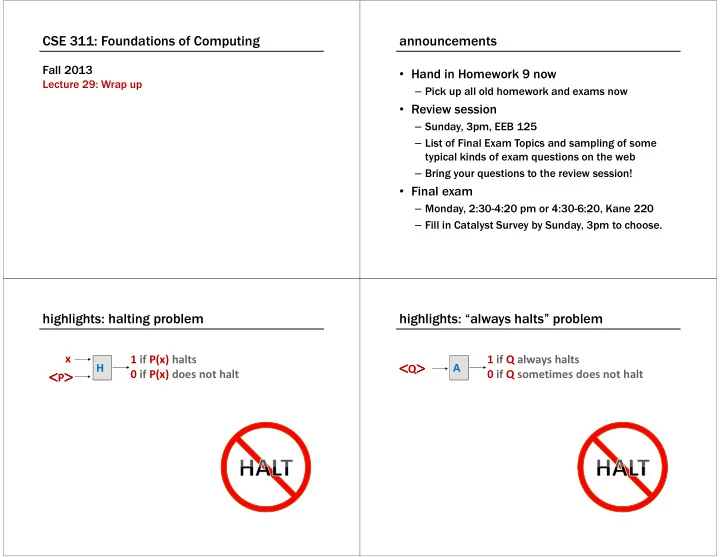
CSE 311: Foundations of Computing announcements Fall 2013 • Hand in Homework 9 now Lecture 29: Wrap up – Pick up all old homework and exams now • Review session – Sunday, 3pm, EEB 125 – List of Final Exam Topics and sampling of some typical kinds of exam questions on the web – Bring your questions to the review session! • Final exam – Monday, 2:30-4:20 pm or 4:30-6:20, Kane 220 – Fill in Catalyst Survey by Sunday, 3pm to choose. highlights: halting problem highlights: “always halts” problem x 1 if P(x) halts 1 if Q always halts < Q > < < < > > > H A 0 if P(x) does not halt 0 if Q sometimes does not halt < P > < < < > > >
the “always ERROR” problem the “always ERROR” problem • Given: Given: Given: Given: <R R R R>, the code of a program R R R R 1 if Q always halts < Q > < < < > > > HALT A • Output: Output: Output: Output: 1 1 1 1 if R R R always prints ERROR R 0 if Q does not always halt 0 if R 0 0 0 R does not always print ERROR R R Suppose we had a TM E for the ERROR problem < < R > < < > > > 1 if Q always Convert’ E < Q > < < < > > > halts Q’s code 0 if Q does not Q’s code … … always halt end of Q end of Q Print ERROR program equivalence general phenomenon: can’t tell a book by its cover Input: the codes of two programs, <P P P> and <Q P Q Q Q> Rice’s Theorem: Rice’s Theorem: Rice’s Theorem: In general there is no way to tell Rice’s Theorem: anything about the input/output (I I/O I I O O) behavior of a O Output: 1 1 if P 1 1 P P produces the same output P program P P just given its code <P P P P P P>! as Q Q Q Q does on every input 0 0 0 0 otherwise
quick lessons CSE 311: Foundations of Computing Fall 2013 • Don’t rely on the idea of improved compilers The 10 minute version and programming languages to eliminate major programming errors – truly safe languages can’t possibly do general computation • Document your code!!!! – there is no way you can expect someone else to figure out what your program does with just your code ....since....in general it is provably impossible to do this! about the course propositional logic • From the CSE catalog: • Statements with truth values – CSE 311 Foundations of Computing I (4 CSE 311 Foundations of Computing I (4 CSE 311 Foundations of Computing I (4 CSE 311 Foundations of Computing I (4) ) ) ) – The Washington State flag is red Examines fundamentals of logic, set theory, – It snowed in Whistler, BC on January 4, induction, and algebraic structures with 2011. – Rick Perry won the Iowa straw poll applications to computing; finite state – Space aliens landed in Roswell, New machines; and limits of computability. Mexico Prerequisite: CSE 143; either MATH 126 or – If n is an integer greater than two, then the equation a n + b n = c n has no MATH 136. solutions in non-zero integers a, b, and c. • What this course is about: Negation (not) ¬ p – Propositional variables: p, q, r, s, . . . Conjunction (and) p ∧ q – Foundational structures for the practice of – Truth values: T T T T for true, F F for false F F Disjunction (or) p ∨ q computer science and engineering – Compound propositions Exclusive or p ⊕ q Implication p → q Biconditional p ↔ q
english and logic logical equivalence • You cannot ride the roller coaster if you are • Terminology: A compound proposition is a under 4 feet tall unless you are older than – Tautology if it is always true 16 years old – Contradiction if it is always false – Contingency if it can be either true or false – q : you can ride the roller coaster – r : you are under 4 feet tall p ∨ ∨ ∨ ∨ ¬ ¬ ¬ ¬ p – s : you are older than 16 p ⊕ p ( p → q ) ∧ p ( r ∧ ¬ s ) → ¬ q ( p ∧ q ) ∨ ( p ∧ ¬ q ) ∨ ( ¬ p ∧ q ) ∨ ( ¬ p ∧ ¬ q ) logical equivalence digital circuits • p and q are logically equivalent iff • Computing with logic p ↔ q is a tautology – T T corresponds to 1 or “high” voltage T T • The notation p ≡ q denotes p and q are logically – F F F F corresponds to 0 or “low” voltage equivalent • Gates – Take inputs and produce outputs • De Morgan’s Laws: Functions – Several kinds of gates ¬ (p ∧ q) ≡ ¬ p ∨ ¬ q – Correspond to propositional connectives ¬ (p ∨ q) ≡ ¬ p ∧ ¬ q Only symmetric ones (order of inputs irrelevant)
combinational logic circuits a simple example: 1-bit binary adder Cout Cin • Inputs: A, B, Carry-in A A A A A • Outputs: Sum, Carry-out B B B B B AND S S S S S OR A S B A B Cin Cout S AND Cout 0 0 0 0 0 Cin 0 0 1 0 1 0 1 0 0 1 0 1 1 1 0 Cout = B Cin + A Cin + A B 1 0 0 0 1 1 0 1 1 0 Wires can send one value to multiple gates S = A’ B’ Cin + A’ B Cin’ + A B’ Cin’ + A B Cin 1 1 0 1 0 1 1 1 1 1 = A’ (B’ Cin + B Cin’ ) + A (B’ Cin’ + B Cin ) = A’ Z + A Z’ = A xor Z = A xor (B xor Cin) boolean algebra sum-of-products canonical forms • Also known as disjunctive normal form • An algebraic structure consists of • Also known as minterm expansion – a set of elements B George Boole – 1854 – binary operations { + , • } F = 001 011 101 110 111 – and a unary operation { ’ } F = + A’BC + AB’C + ABC’ + ABC A’B’C – such that the following axioms hold: A B C F F’ 0 0 0 0 1 1. the set B contains at least two elements: a, b 0 0 1 1 0 2. closure: a + b is in B a • b is in B 0 1 0 0 1 0 1 1 1 0 3. commutativity: a + b = b + a a • b = b • a 1 0 0 0 1 4. associativity: a + (b + c) = (a + b) + c a • (b • c) = (a • b) • c 1 0 1 1 0 5. identity: a + 0 = a a • 1 = a 1 1 0 1 0 6. distributivity: a + (b • c) = (a + b) • (a + c) a • (b + c) = (a • b) + (a • c) F’ = A’B’C’ + A’BC’ + AB’C’ 1 1 1 1 0 7. complementarity: a + a’ = 1 a • a’ = 0
predicate calculus statements with quantifiers • ∀ x (Even( x ) ∨ Odd( x )) • Predicate or Propositional Function Domain: Positive Integers – A function that returns a truth value Even( x ) • ∃ x (Even( x ) ∧ Prime( x )) Odd( x ) • “ x is a cat” Prime( x ) Greater( x , y ) • “student x has taken course y ” Equal( x , y ) • ∀ x ∃ y (Greater( y , x ) ∧ Prime( y )) • “ x > y ” • ∀ x P(x) : P(x) is true for every x in the • ∀ x (Prime( x ) → (Equal( x , 2) ∨ Odd( x )) domain • ∃ x P(x) : There is an x in the domain for • ∃ x ∃ y (Equal( x, y + 2) ∧ Prime( x ) ∧ Prime( y )) which P(x) is true proofs simple propositional inference rules • Start with hypotheses and facts • Excluded middle ∴ p ∨¬ p • Use rules of inference to extend set of facts • Two inference rules per binary connective one to • Result is proved when it is included in the eliminate it, one to introduce it. set p ∧ q p, q ∴ p, q ∴ p ∧ q p p ∨ q , ¬ p ∴ p ∨ q, q ∨ p ∴ q p ⇒ q Direct Proof Rule p, p → q ∴ p → q ∴ q
inference rules for quantifiers even and odd Even(x) ≡ ∃ ∃ y (x=2y) ∃ ∃ Odd(x) ≡ ∃ ∃ y (x=2y+1) ∃ ∃ Domain: Integers P(c) for some c ∀ x P(x) • Prove: “The square of every odd number is odd” ∴ ∃ x P(x) ∴ P(a) for any a English proof of: ∀ x (Odd(x) → Odd(x 2 )) Let x be an odd number. “Let a be anything”...P(a) ∃ x P(x) Then x=2k+1 for some integer k (depending on x) ∴ ∀ x P(x) ∴ P(c) for some special c Therefore x 2 =(2k+1) 2 = 4k 2 +4k+1=2(2k 2 +2k)+1. Since 2k 2 +2k is an integer, x 2 is odd. � characteristic vectors one-time pad • Let U = {1, . . ., 10}, represent the set • Alice and Bob privately share random n-bit vector K {1,3,4,8,9} with – Eve does not know K • Later, Alice has n-bit message m to send to Bob 1011000110 • Bit operations: – Alice computes C = m ⊕ K – 0110110100 ∨ 0011010110 = 0111110110 – Alice sends C to Bob • ls –l – Bob computes m = C ⊕ K which is (m ⊕ K) ⊕ K drwxr-xr-x ... Documents/ • Eve cannot figure out m from C unless she can guess K -rw-r--r-- ... file1
Recommend
More recommend
Explore More Topics
Stay informed with curated content and fresh updates.