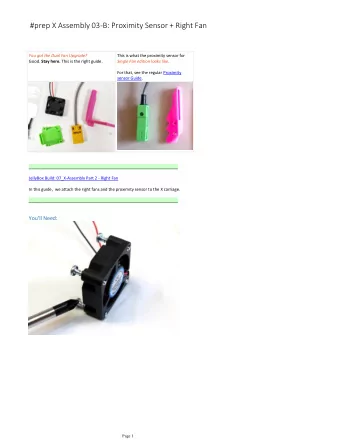
Proximity Sensors n The central task is to determine P(z|x) , i.e., - PDF document

Beam Sensor Models Pieter Abbeel UC Berkeley EECS Many slides adapted from Thrun, Burgard and Fox, Probabilistic Robotics Proximity Sensors n The central task is to determine P(z|x) , i.e., the probability of a measurement z given that the robot is at position x . n Question : Where do the probabilities come from? n Approach : Let ’ s try to explain a measurement. 2 Page 1 �

Beam-based Sensor Model n Scan z consists of K measurements. z = { z , z ,..., z } 1 2 K n Individual measurements are independent given the robot position. K P ( z | x , m ) P ( z | x , m ) ∏ = k k 1 = 3 Beam-based Sensor Model K P ( z | x , m ) P ( z | x , m ) ∏ = k k 1 = 4 Page 2 �

Typical Measurement Errors of an Range Measurements 1. Beams reflected by obstacles 2. Beams reflected by persons / caused by crosstalk 3. Random measurements 4. Maximum range measurements 5 Proximity Measurement n Measurement can be caused by … n a known obstacle. n cross-talk. n an unexpected obstacle (people, furniture, …). n missing all obstacles (total reflection, glass, …). n Noise is due to uncertainty … n in measuring distance to known obstacle. n in position of known obstacles. n in position of additional obstacles. n whether obstacle is missed. 6 Page 3 �

Beam-based Proximity Model Measurement noise Unexpected obstacles 0 z exp z max z exp 0 z max 2 z ( z z exp ) e − λ z z 1 − ⎧ η λ < ⎫ 1 − exp P ( z | x , m ) P ( z | x , m ) e = 2 b ⎨ ⎬ = η unexp hit 0 otherwise 2 b π ⎩ ⎭ 7 Beam-based Proximity Model Random measurement Max range 0 z exp z max 0 z exp z max 1 1 P ( z | x , m ) P ( z | x , m ) = η = η max rand z z small max 8 Page 4 �

Resulting Mixture Density T P ( z | x , m ) α ⎛ ⎞ ⎛ ⎞ hit hit ⎜ ⎟ ⎜ ⎟ P ( z | x , m ) α ⎜ ⎟ ⎜ ⎟ unexp unexp P ( z | x , m ) = ⋅ ⎜ ⎟ ⎜ ⎟ P ( z | x , m ) α max max ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ P ( z | x , m ) α ⎝ ⎠ ⎝ ⎠ rand rand How can we determine the model parameters? 9 Raw Sensor Data Measured distances for expected distance of 300 cm. Sonar Laser 10 Page 5 �

Approximation n Maximize log likelihood of the data P ( z | z ) exp n Search space of n-1 parameters. n Hill climbing n Gradient descent n Genetic algorithms n … n Deterministically compute the n-th parameter to satisfy normalization constraint. 11 Approximation Results Laser 300cm 400cm Sonar 12 Page 6 �

Example z P(z|x,m) 13 Approximation Results Laser Sonar 15 Page 7 �

Influence of Angle to Obstacle "sonar-0" 0.25 0.2 0.15 0.1 0.05 0 70 0 10203040506070 0 10 20 30 40 50 60 16 Influence of Angle to Obstacle "sonar-1" 0.3 0.25 0.2 0.15 0.1 0.05 0 70 0 10203040506070 0 10 20 30 40 50 60 17 Page 8 �

Influence of Angle to Obstacle "sonar-2" 0.3 0.25 0.2 0.15 0.1 0.05 0 70 0 10203040506070 0 10 20 30 40 50 60 18 Influence of Angle to Obstacle "sonar-3" 0.25 0.2 0.15 0.1 0.05 0 70 0 10203040506070 0 10 20 30 40 50 60 19 Page 9 �

Summary Beam-based Model n Assumes independence between beams. n Justification? n Overconfident! n Models physical causes for measurements. n Mixture of densities for these causes. n Assumes independence between causes. Problem? n Implementation n Learn parameters based on real data. n Different models should be learned for different angles at which the sensor beam hits the obstacle. n Determine expected distances by ray-tracing. n Expected distances can be pre-processed. 20 Page 10 �