Principles of Programming Languages h"p://www.di.unipi.it/~andrea/Dida2ca/PLP-15/ Prof. Andrea Corradini Department of Computer Science, Pisa Lesson 17 � • Loops in Control Flow Graphs – Convergence speed of data-flow analysis • Region based Data-Flow analysis • Symbolic analysis
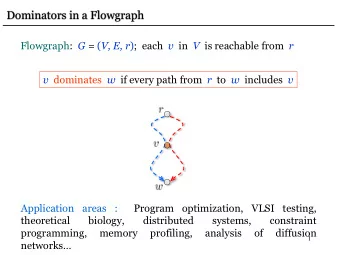
Determining Loops in Flow Graphs: Dominators • Dominators : d dom n – Node d of a CFG dominates node n if every path from the entry node to n goes through d – The loop entry dominates all nodes in the loop • The immediate dominator m of a node n is the last dominator of n on any path from the iniGal node to n – If d ≠ n and d dom n then d dom m • Since each node has a unique immediate dominator , dominators form a tree 2
Dominator Tree of a CFG 1 1 2 2 3 3 4 4 5 6 7 5 6 8 7 9 10 8 9 10 CFG Dominator tree 3
Data-Flow Analysis for Dominators • The set of dominators for each node n , D(n) , can be computed with dataflow analysis • Fact: d dom n iff d = n or d dom m for all m in pred(n) d – DirecGon: forwards … P k P 1 P 2 – SemilaUce: powerset of CFG nodes n – Transfer funcGon: f B (x) = x U {B} – Meet operator: intersecGon ( must ) – Boundary: OUT[ENTRY] ={ENTRY} – IniGalizaGon: OUT[B] = all Nodes 4
Natural Loops • A back edge in a CFG is an edge a → b where b dominates a • A natural loop: – has a single-entry node d , the header , which dominates all nodes in the loop – has a back edge that enters node d • Given a back edge n → d – Its natural loop consists of d plus the nodes that can reach n without going through d – The loop header is node d 5
Reducible Flow Graphs • A flow graph is reducible if and only if deleGng all back edges the resulGng graph is acyclic. • We consider only CFGs which are reducible 1 2 1 3 2 3 4 Example of a � nonreducible CFG � Example of a � (not a natural loop: no back edge to dominator 1) reducible CFG 6
Natural Inner/Outer Loops • In reducible CFGs, unless two loops have the same header, they are disjoint or one is nested within the other • A nested loop is an inner loop if it contains no other loops • A loop is an outer loop if it is not contained within another loop 7
Natural Inner/Outer Loops Example Natural loop � 1 for 1 dom 9 1 2 Natural loop � 2 3 for 3 dom 4 3 4 Natural loop � 1 4 5 6 for 4 dom 7 Natural loop � 5 6 2 3 7 for 3 dom 8 7 4 8 Natural loop � 5 6 7 8 9 10 for 7 dom 10 9 10 8 9 10 CFG CFG Dominator tree 8
Depth of a Control Flow Graph 1 • Depth: largest 1 2 number of back 2 3 3 edges in any acyclic 4 4 path in the graph 5 6 7 5 6 • IntuiGon: not larger 8 7 than the maximal 9 10 8 nesGng of loops 9 10 9
Speed of convergence of data-flow analysis • Maximum number of iteraGons: (height of the laUce) x (number of nodes) • If value of interest can be propagated along acyclic path (like for reaching definiEons, available expressions, live variables ), few passes are sufficient in general, depending on number of loop nesGng (typically, depth of CFG + 1). • Otherwise, several iteraGons in loops might be needed: eg. constant folding L: x = y; y = z; z = 1; goto L 10
Region-Based Analysis • In dataflow analysis, transfer funcGons are associated with basic blocks • Here we associate them with regions, which provide a hierarchical view on the program • Proceeds from smaller to larger regions, up to enGre procedures • Need more algebraic structure: – SemilaUce of values – SemilaUce of transfer funcGons with meet , composiEon and closure operator 11
Regions • A region is a porGon of the flow graph with a single entry point. – A single statement of a high-level language is a region – Each block or other form of statement nesGng is a region • A region is a collecGon of nodes N and edges E such that – N has a dominator h – No node external of N can reach a node m in N without passing through h – E contains all edges between nodes in N (but, possibily, for some to h) • Note: natural loops are regions, but regions may not contain loops 12
Region hierarchies • AssumpGon: the CFG is reducible (thus natural loops are disjoint or nested) • Building the region hierarchy for the CFG: – Every block is a leaf region – For each natural loop L , starGng from the innermost, replace the body (all nodes and edges but for back edges to the header) of L with a new node represenGng a region R . All edges from L become edges from R, possibly loops. R is a body region . – Construct the loop region R’ , that is idenGcal to R but without the loop: it represents the whole L – Finally construct one region for the resulGng acyclic flow graph, if needed 13
Recommend
More recommend
