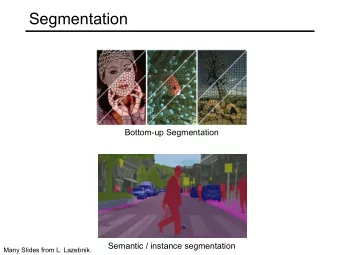
Physics of MRF Regularization for Segmentation of Materials - PowerPoint PPT Presentation

Physics of MRF Regularization for Segmentation of Materials Microstructure Images Jeff Simmons† Craig Przybyla† Stephen Bricker‡ Dae Woo Kim* Mary Comer* †Materials and Manufacturing Directorate; Air Force Resaerch Laboratory; OH 45433; USA ‡Department of Electrical and Computer Engineering; University of Dayton; OH 45469; USA *Department of Electrical and Computer Engineering; Purdue University; IN 47907 Distribution A (Unlimited Distribution) 88ABW-2014-3260

Electronic Imaging for Microscopy-2005 to Date Incorporate and adapt modern imaging methods for analysis of microscope data Materials EE/Comp. Sci Marc De Graef (CMU) Charles Bouman, Mary Comer, Craig Przybyla, Ilya Pollak (Purdue) Lawrence Drummy, Alfred Hero (U. Mich) Jeff Simmons (AFRL) Song Wong (U. South Carolina) Russel Hardie (U. Dayton) Bayesian Segmentation Dictionary-based inversion (EM/MPM) (EBSD) Comer Hero Graphcut Segmentation Anomaly detection (topology preserving) (automatic classification of EBSD Wong Irregular features in large datasets) Hero, Hardie Dictionary matching segmentation Feature Extraction (matching persuits) (velocity gradient Pollak moment invariant texture classifications) Przybyla, De Graef Stabilized inverse diffusion (discontinuities) TEM Tomographic reconstruction (SIDE) (HAADF STEM, bright field TEM) Pollak Drummy, Bouman ...always outdated Distribution A (Unlimited Distribution) 88ABW-2014-3260

Opportunity: Co-Evolution of the Ising Model Physics Ising (1924) 1-D Ising Ferromagnet model Onsager (1944) 2-D Ising Ferromagnet model Potts (1952) Extension to multiple spin states Hammersley&Clifford(1971) Binder (1968) general method for MRF priors Metropolis M/C-thermodynamics Liebowitz, et al. (1976) Besag (1974) Ising spin systems proof of H-C theorem Srolovitz, Rollett, Holm, et al. (1988) German and German(1984) Evolution of poly-crystalline mat’ls MC/MC MAP est. Miodownik, et al. (2000) Marroquin, et al. (1987) second phase pinning Gibbs Sampler MPM Statistics/Imaging Materials Distribution A (Unlimited Distribution) 88ABW-2014-3260

Motivation Research Trends Evolution Modeling Digital Microscopy Integrated Computational Materials Engineering Conventional Microscopy 1980 1990 2000 2010 Opportunity Fusion of evolution modeling with digital microscopy parameter estimation for evolution models physics-based regularization for image analysis Presentation Show where MRF regularization ⇔ real material behavior Goals Uncover unexploited materials properties implicit in MRF Distribution A (Unlimited Distribution) 88ABW-2014-3260

Outline Motivation Integration of techniques Legacy: evolution models Emerging: digital microsopy Methods EM/MPM regularized segmentation Physics-dominated extreme Surface Science `Energy penalty’ ⇒ `interfacial energy’ Coarse graining Physics in MRF Materials physics intrinsic in MRF regularization Commonly observed phenomena Segmentations Qualitative Potential Developments Physics not in conventional MRF regularization Materials specific extensions Conclusions Distribution A (Unlimited Distribution) 88ABW-2014-3260

Methods EM/MPM Forward model mixture of Gaussians Segmentation EM algorithm for fitting histogram Comer and Delp, (2000) N − ( y r − µ x r ) 2 1 exp f Y |X ( y |x , θ ) = 2 σ 2 2 πσ 2 x r x r r =1 Regularization 4-neighbor MRF p X ( x ) = 1 z exp − β x r ,x s (1 − δ x r ,x s ) { r,s } ∈ C δ ij = Kronekar delta C = 4-neighbor clique Estimation of posterior marginals Markov chain Monte Carlo Phantoms Slight composition gradients + Poisson noise artifact boundaries: pure physics Distribution A (Unlimited Distribution) 88ABW-2014-3260

Extremes of Regularization 100% 100% Observation Physics Regularization Strong Large hyperparameter Regularization Low contrast Regularization Dominated Segmentation Gradient Segmentation histogram model + Poisson noise Artifact boundary (mixture of Gaussians model) Distribution A (Unlimited Distribution) 88ABW-2014-3260

Surface Science 101 1/2: Coarse Graining Markov Random Field (p X ) Coarse-Graining: β → Γ 1/z exp [ - Σ ij β αβ ( 1 - δ αβ ij ) ] Energy = β l/ Δ y Smoothing: penalty unless both pixels are same class l/cos θ β αβ spatial interaction parameters l dependent on classes involved Anisotropic interface energy density Δ y = Δ x θ I = pixel dimension n t e r f a c e Γ θ Energy density: horizontal ( β / Δ y ) cos θ Energy density: vertical Wulff plot for 4-neighbor ( β / Δ x ) sin θ interfacial energy Total interfacial energy density Γ 0°Κ = √2 ( β / Δ y ) sin ( θ + π /4 ) θ ∈ [ 0, π/2 ] Distribution A (Unlimited Distribution) 88ABW-2014-3260

Surface Science 101 2/2: Interface `Tension’ `Energy’ ⇒ `force’ Regularizing boundary with `energy’ ⇒ E( P ) ⇒ F = ∇ E( P ) Equilibrium ⇒ F = 0 v 2 v i = 0 Γ i i P P v i = vector from P in direction of boundary v 1 dE i Γ i d v i v 3 Example Fig. 6 of Gari Arutinov, et al., J. Micromech. Microeng., 22, 115022, (2012). Oxidized SiO 2 substrate Gold coated SiO 2 substrate Distribution A (Unlimited Distribution) 88ABW-2014-3260

Surf. Sci. in MRF-Regularized Segmentations Capillarity Surface energy induced lifting of one phase extending region with interface length penalty Wetting Coating phases with `boundary phase’ thin region separating two larger regions of different classes Pinning Pinning interaction of boundaries with regions Distribution A (Unlimited Distribution) 88ABW-2014-3260

Capillarity Lifting ρ = 2( Γ vg - Γ lg - Γ vl cos θ )/dh Physics Γ vg l v Γ Static Head l (h) Γ lg θ (density ρ ) Capillary Diameter (d) Regularized Segmentation β = 1.4 β = 1.4 β = 2.0 artifact static head β = 2.0 β = 1.4 β = 1.4 Phantom Distribution A (Unlimited Distribution) 88ABW-2014-3260

Wetting Mo grains at two different temperatures interfacial energy fn of temperature Non-wet interfaces Wet interfaces SEM image Cross-sectional SEM image Mo-12.4%Ni quenched from 1344C Mo-12.4%Ni quenched from 1495C Courtesy Jian Luo Xiaomeng Shi and Jian Luo, Appl. Phys. Lett., 94, 251 908, (2009) Distribution A (Unlimited Distribution) 88ABW-2014-3260

Thin Region Separating Two Regions class 2 class 1 class 0 Segmented image Segmented image β 0,1 =0.9, β 0,2 = 0.5 , β 1,2 = 0.9 β 0,1 =0.9, β 0,2 = 0.9 , β 1,2 = 1.8 non-wet interface wet interface Raw image SiC fiber in SiC matrix. BN coating Imaging: optical slight intensity gradient in BG Distribution A (Unlimited Distribution) 88ABW-2014-3260

Ex 2: Zener Pinning for Grain Refjnement Friction Force Interface `attracted to’ particles Reduces boundary penalty l Γ r Γ E = 2 π r Γ + l Γ - 2r Γ E = 2 π r Γ + l Γ `Friction force’ of 2 r Γ pinning the boundary Zener Pinning Used in alloy design stop grains from growing Mechanism Zener, unpublished (cited C.S. Smith, 1948) Source: commons.wikimedia.com (Zener Pinning) Distribution A (Unlimited Distribution) 88ABW-2014-3260

Interaction of Boundaries with Regions Individual particles in image `pin’ boundary Boundary intersects large black classes at right angles Distribution A (Unlimited Distribution) 88ABW-2014-3260

Future Materials-Specifjc Extensions Anisotropic interfacial energy cusps imply torques Γ θ 8-neighbor has cusps in [1 1] directions 1 2 Coarse graining: quantitative link to materials Γ can be estimated from β with Monte Carlo (Binder) Requires a `temperature’ of the MRF Thermodynamics Statistical Mechanics T = RMS ( E ) F = E - T H k b Nc v Wetting: potential robust segmentation experiment: boundries between same classes class 1 class 0 Distribution A (Unlimited Distribution) 88ABW-2014-3260

Conclusions MRF is a generalization of Ising Model solid state physics Reproduces classical surface science qualitative Materials-specific extensions possible Ising model reflects actual materials behavior Expected uses inpainting boundary orientations quatititative regularization separation of spatially close regions in segmentations Distribution A (Unlimited Distribution) 88ABW-2014-3260