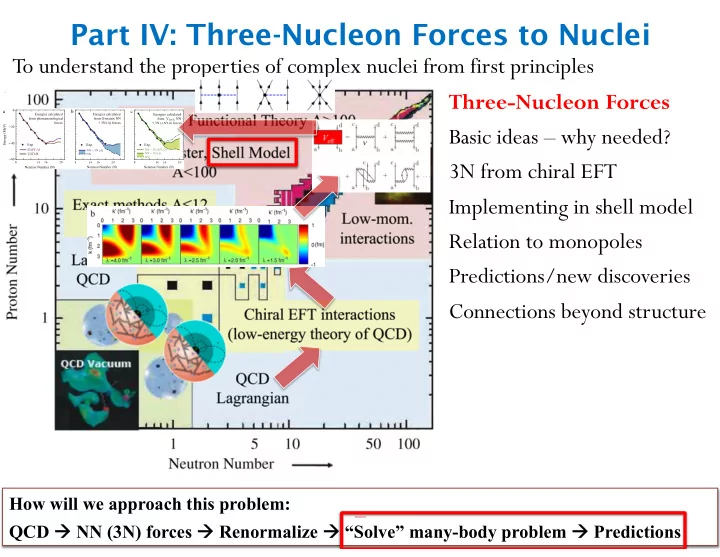
Part IV: Three-Nucleon Forces to Nuclei To understand the properties - PowerPoint PPT Presentation

Part IV: Three-Nucleon Forces to Nuclei To understand the properties of complex nuclei from first principles Three-Nucleon Forces a b c Basic ideas – why needed? 3N from chiral EFT Implementing in shell model Relation to monopoles Predictions/new discoveries Connections beyond structure How will we approach this problem: QCD à à NN (3N) forces à à Renormalize à à “Solve” many-body problem à à Predictions

Chiral Effective Field Theory: Nuclear Forces Nucleons interact via pion exchanges and contact interactions Consistent treatment of NN, 3N,… NN couplings fit to scattering data Δ (1232) Weinberg, van Kolck, Kaplan, Savage, Wise

Chiral EFT: N 2 LO 3N First non-vanishing 3N contributions: Next-to-next-to-leading order ν = 3 2 � 3 � = g A � � 1 · q � 1 � � 3 · q � 3 2 2 �� � 1 · � 3 � − 4 c 1 M � V 3 N 2 + M � 2 + M � 4 2 �� q 3 � q 1 8 F � � 3 � + c 4 � 1 � � 3 · � 2 q � 2 � � 1 � q � 3 · � + 2 c 3 q � 1 · q � � 3 · q � 3 + 1 − g A D � 3 2 � 1 · � 3 � � 1 · q 2 E � 2 · � 3 , 2 + M � 2 8 F � q 3

Chiral EFT: N 2 LO 3N First non-vanishing 3N contributions: Next-to-next-to-leading order ν = 3 2 � 3 � = g A � � 1 · q � 1 � � 3 · q � 3 2 2 �� � 1 · � 3 � − 4 c 1 M � V 3 N 2 + M � 2 + M � 4 2 �� q 3 � q 1 8 F � � 3 � + c 4 � 1 � � 3 · � 2 q � 2 � � 1 � q � 3 · � + 2 c 3 q � 1 · q � � 3 · q � 3 + 1 − g A D � 3 2 � 1 · � 3 � � 1 · q 2 E � 2 · � 3 , 2 + M � 2 8 F � q 3 Three undetermined π N couplings from NN fit

Chiral EFT: N 3 LO 3N Next-to-next-to-next-to-leading order ν = 4 Good news: no new constants Bad news: well, there’s all this

Aside: Effects of Adding Explicit Deltas ������������� �������������������������������� ��� � � �� ���������������������������������� � � �� ���������������������������������� ������������������������������������������������������� no effect up to N 2 LO (modulo reshuffling) � � �� expect large contributions to the ring & 2 π -1 π -topologies saturating some of the ����������������������������������������������� N 4,5,6 LO graphs in the Δ -less theory What is more efficient: Δ -less N 4 LO (and beyond?) vs Δ -full N 3 LO ?? � π - � π ���� � π Reshuffles effects to different chiral orders

SRG Evolution in HO Basis Most common to SRG evolve 3N in HO basis: 3B-Jacobi HO matrix elements � = 0 . 00 fm 4 � = ∞ fm � 1 � � 0 � E � � � JT � E � JT � � � H � � T int � + , T = 1 J � = 1 2 , � Ω = 24 MeV 2 E � � NCSM ground state 3 H 18 � 20 -6.5 ( E � , � � ) � 22 0 -7 E [MeV] 24 0.12 -7.5 � 0.32 [MeV] 26 -8 0.64 � � 1.16 � � � � � 28 -8.5 . 0 4 8 12 16 20 24 28 2 0 � E � 18 20 22 24 26 28 N m �� ( E, � ) 1) SRG-evolve both NN and 3N: NN+3N-full 2) NN Vlowk, refit 3N: NN+3N-fit

SRG Evolution in HO Basis Most common to SRG evolve 3N in HO basis: 3B-Jacobi HO matrix elements � = 0 . 02 fm 4 � = 2 . 66 fm � 1 � � 0 � E � � � JT � E � JT � � � H � � T int � + , T = 1 J � = 1 2 , � ٠= 24 MeV 2 E � � NCSM ground state 3 H 18 � 20 -6.5 ( E � , � � ) 22 � 0 -7 E [MeV] 24 0.12 -7.5 � 0.32 [MeV] 26 0.64 -8 � � 1.16 � � � � � � � � 28 -8.5 . 0 4 8 12 16 20 24 28 2 0 � E � 18 20 22 24 26 28 N m �� ( E, � ) 1) SRG-evolve both NN and 3N: NN+3N-full 2) NN Vlowk, refit 3N: NN+3N-fit

SRG Evolution in HO Basis Most common to SRG evolve 3N in HO basis: 3B-Jacobi HO matrix elements � = 1 . 28 fm 4 � = 0 . 94 fm � 1 � � 0 � E � � � JT � E � JT � � � H � � T int � + , T = 1 J � = 1 2 , � ٠= 24 MeV 2 E � � NCSM ground state 3 H 18 � 20 -6.5 ( E � , � � ) 22 � 0 -7 E [MeV] 24 0.12 -7.5 0.32 [MeV] 26 � -8 0.64 � � 1.16 � � � � � � � � � � 28 -8.5 . 0 4 8 12 16 20 24 28 2 0 � E � 18 20 22 24 26 28 N m �� ( E, � ) 1) SRG-evolve both NN and 3N: NN+3N-full 2) NN Vlowk, refit 3N: NN+3N-fit

Induced 3N Forces Effect of including 3N-ind? Exactly initial up to neglected 4N-ind V NN − 24 − 7.4 4 He 3 H NN-only 3 LO (500 MeV) N Ground-State Energy [MeV] − 7.6 NN + NNN-induced Ground-State Energy [MeV] − 25 − 7.8 − 26 − 8.0 NN-only − 27 3 LO (500 MeV) NN+NNN-induced N − 8.2 − 28 Expt. − 8.4 Expt. − 29 − 8.6 1 2 3 4 5 6 7 10 20 1 2 3 4 5 10 20 − 1 ] − 1 ] λ [fm λ [fm NN-only clear cutoff dependencs 3N-ind: dramatic reduction in cutoff dependence, no agreement with experiment

Induced 3N Forces Effect of including 3N-ind? Exactly initial up to neglected 4N-ind V NN − 24 − 24 − 7.4 − 7.4 4 He 4 He 3 H NN-only 3 H NN-only 3 LO (500 MeV) 3 LO (500 MeV) N N NN + NNN-induced Ground-State Energy [MeV] − 7.6 − 7.6 NN + NNN-induced Ground-State Energy [MeV] Ground-State Energy [MeV] Ground-State Energy [MeV] − 25 − 25 NN + NNN − 7.8 − 7.8 − 26 − 26 − 8.0 − 8.0 NN-only NN-only − 27 − 27 NN+NNN-induced NN+NNN-induced 3 LO (500 MeV) N +NNN-initial − 8.2 − 8.2 − 28 − 28 Expt. Expt. − 8.4 − 8.4 Expt. Expt. − 29 − 8.6 − 29 − 8.6 1 5 6 7 1 2 3 4 5 10 20 2 3 4 10 20 1 2 3 4 5 6 7 10 20 1 2 3 4 5 10 20 − 1 ] − 1 ] − 1 ] − 1 ] λ [fm λ [fm λ [fm λ [fm NN-only clear cutoff dependencs 3N-ind: dramatic reduction in cutoff dependence, no agreement with experiment NN+3N-full retains cutoff independence, reproduces experiment!

Benefits of Lower Cutoffs Use cutoff dependence to assess missing physics: return to Tjon line Varying cutoff moves along line Still never reaches experiment Tool, not a parameter! ing

Benefits of Lower Cutoffs Use cutoff dependence to assess missing physics: return to Tjon line Varying cutoff moves along line Tjon line for NN-only potentials 30 Still never reaches experiment SRG NN-only − 1 ) SRG NN+NNN ( λ >1.7 fm 29 Tool, not a parameter! λ =1.8 4 He) [MeV] Expt. λ =1.5 Including 3N reaches expt. 28 λ =2.0 λ =2.5 27 Why not perfect fit? λ =1.2 λ =3.0 E b ( 26 28.4 ing 3 LO N 28.3 25 (500 MeV) 28.2 8.45 8.5 24 7.6 7.8 8 8.2 8.4 8.6 8.8 3 H) [MeV] E b (

Cutoff Variation with 3N Forces Use cutoff variation to assess missing physics in few body systems Radii of triton and alpha particle calculated from NN+3N forces Minimal cutoff variation

Chiral Three-Body Forces in Light Nuclei Importance of chiral 3N forces established in light nuclei Converged NCSM (Navratil 2007) They work! What about nuclear matter?

Perturbative in Symmetric Nuclear Matter? H ( Λ ) = T + V NN ( Λ ) + V 3N ( Λ ) + V 4N ( Λ ) + · · · Yes, but if I remember, saturation isn’t correct Significant improvement with low-momentum interactions!

Perturbative in Symmetric Nuclear Matter? H ( Λ ) = T + V NN ( Λ ) + V 3N ( Λ ) + V 4N ( Λ ) + · · · empirical Now NN+3N-fit remain perturbative and reproduce saturation! Minor but non-negligible cutoff variation

3N Forces for Valence-Shell Theories Normal-ordered 3N : contribution to valence neutron interactions Effective two-body Effective one-body 16 16 O core O core a V 3 N ,eff a ' = 1 ∑ ab V 3 N ,eff a ' b ' = α ab V 3 N α a ' b ' ∑ αβ a V 3 N αβ a ' 2 α = core αβ = core Combine with microscopic NN: eliminate empirical adjustments

3N Forces for Valence-Shell Theories Effects of residual 3N between 3 valence nucleons? Normal-ordered 3N : microscopic contributions to inputs for CI Hamiltonian Effects of residual 3N between 3 valence nucleons? Coupled-Cluster theory with 3N: benchmark of 4 He 0- 1- and 2-body of 3NF dominate Residual 3N can be neglected Work on 16 O in progress Hagen, Papenbrock et al . (2007) Approximated residual 3N by summing over valence nucleon – Nucleus-dependent: effect small, not negligible by 24 O

Two-body 3N: Monopoles in sd -shell 1 Dominant effect from 0.5 T=1 one- Δ – as expected 0 from cutoff variation V(ab;T) [MeV] -0.5 3N forces produce clear -1 repulsive shift in monopoles V low k -1.5 +3N ( Δ ) -2 2 LO) + 3N (N -2.5 USDa USDb -3 -3.5 d5d5 d5d3 d5s1 d3d3 d3s1 s1s1 First calculations to show missing monopole strength due to neglected 3N Future : Improved treatment of high-lying orbits

Oxygen Anomaly First calculations using NN+3N Probe limits of nuclear existence with 3N forces F dripline 3N repulsion amplified with N: crucial for neutron-rich nuclei ? d 3/2 unbound at 24 O with 3N forces 4 Single-Particle Energy (MeV) 2 (d) V NN + 3N ( ∆ ,N LO ) forces low k 0 d3/2 -4 s 1/2 d5/2 -8 2 NN + 3N (N LO) NN + 3N ( ∆ ) NN 8 14 16 20 Neutron Number ( N ) Otsuka, Suzuki, JDH, Schwenk, Akaishi, PRL (2010)