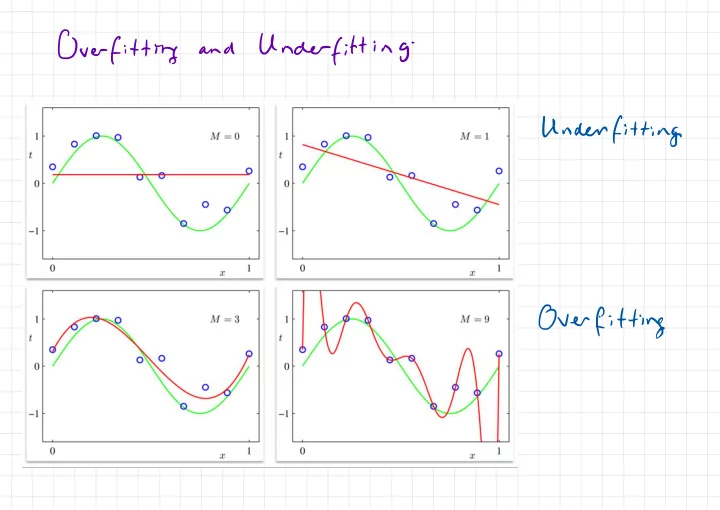

Over fitting Under fitting and - Under fitting Over fitting
distribution functions over Bayesian Regression / " ' i diggllloise dist ' f. fnpc f) fcxn ) - ,N En n=1 + En~ PIE yn = ... , ⇒ of Basis Function Linear • a fix f- ) ' • . • • x x I=×w = Iwaka D ×=tI÷El} := fCInl÷ f ( In ) Tvtocxn ) It In D= ' D t.ae#=t9tEIII1NX1NxDpxl - "
Polynomial Example Basis : Wttcfkn ) w°~p( I N ) En ) I t En~ PIE yn n= = ... , , 4 Reduces linear when ¢ to identity is reg . Polynomial Basis xD ¢d(×n ) = Prior in implies on f functions prior on
Ridge Regression ( Regularization ) LZ ia¥ TEI [ Objective : = IF cyn .it ' wto + wa . , I I=i I = o 10 =
Often Ridge Probabilistic Regression Interpretation : ETE - iii. cyn-wtoc.int ) ' to - wa Maximum Posteriori Estimation a Norm ( 0,62 ) Norm ( o , 5) IT ) En Wd En t ~ yn - = pin log 15 ) pin 15 ) angry ax = argument - ¥155 Pig , hi log ) = anginwax ) tlogpcw log piylw ) = anginwax
often Ridge Probabilistic Regression Interpretation : £ rider ④ I Lte ) ' into btw ¢⇒ ) , yn + - ,n= - . n - . . . log¥e Maximum Posteriori Estimation a Norm ( 0,62 ) Norm ( o , 5) IT ) En Wd En t ~ yn - = Norm ( Bto w--oThi ( In ) 62 ) yn ~ , argwfaxpcw-iys-a-gwyaxlogplyiwstlogp.tw ) ' ku ) ) log piyiwi In yn - = I ( log pins log =
Ridge Regression I Tolka ) S Norm Wdr Norinco ,6 ) ( o S ) En Enn t yn = , log piety ) argue ax D= % D= D= , - = no = o - I observations ) 6 precise → o uninformative prior ) C s → as
Plf 'S ) gf Posterior Predictive - I ) ↳ b 5 Ys Ys Yi ya ° Small D O ooo Distribution # y ° a ooo µ O Large 0 ooo A # y x* = Idf ply # Posterior [ - I f) 't 't ' ly ) Predictive ply pcfly ) previous given y* observations far new
Posterior Predictive Distribution ooo € o hi * f I . b 5 I 43 Ss y , ya ,*y* , ° Small o o 00 I 9--91 , " O I o CO l # y * f , O I Large 0 A # y y* . I f Incorporate about Idea uncertainty predictions in :
Processes Gaussian Informal Definition y Nonparametric " " of : data determined from Formal Nonparametric Distribution View Functions : on f ) fly function PC Mean ~ ° In , :w x ) µ( h( J function ... * • ' ) Covariance - × ,× • . fcx ) • h ) . F GPC µ . ~ YnIF=f~ • . , ( f I Norm ,6 ) ) × Likelihood - prior Posterior ) p( y f) fly , I pcf ) PC : = , :µ in , PC y ) :n ; likelihood Marginal
Processes Gaussian Practical View : Generalization Multivariate Normal of i= 1£ Prior ) pitch I ) function blini flu µ on at values finite [ lil :-. In , Em ) set of points m t ' E " - fetal E ( pi Norm E ) . ,FEmD - n , , . . Norml fu 6 ) Yul E. fan , x Pl5* Predictive pc j*Iy ) : = pigs
Distributions Joint Igf Values Function an Norm I lqY¥ , 1,1ha .*x N M N X N N El x acx.xx.gg ) I I ¥1 - ' ,X* I h ( ) be CX X x , M N M MX M Xl X = ( ME ) - Nord # , pika ) ) x ) pic t.lu#xlhcx:xmtotD . . , . hcxt.xt.fm?:ii...hcx.?.xnyhlxE,I - ( HIM . ,µEn , thx " thx 'm , In ) , ) - . . , . . . I E t E hit E ,X ) ) Now ( pic x ) = - , , kk ,Xlt6I ) Nonmlpikl 4- E ) Norm I EI ~ o n , 't ) I s hfxx tell ,XltdI Y pelxl *
lil Normals Multivariate " Properties of Gaussian Probability for variables density jointly RN NXM N ZE N MXN til , 1¥81 ) :/ pie , f) Norm = perm M M xN MXM ur Norm , A ) Marginals poet a- = Norm ( p ;D B ) pcp 's = N I XX I x N next ' Norm ' If ( I pip A- a ) Conditional 1/5 ; b- E ) = - - , c ) ' A- CT B - Mx M MXN NXM N Xxl
Distribution Predictive Computing the a- B a- I A tuft :¥¥÷D "i¥lK¥ :& * : " B b- D c Predictive values new on ( C Norm ( ' I C ) 4*1 b- 4 a- I CTA B " CT A- nu - - . , - kfxtxlfhlx ,xlt62IJ Norm ( pix ' II - MIN ) 't 't ~ , hlx.xlt62IThk.x.tl ) k(x4x* ) ( lek - \
Distribution Predictive Computing the Y a- B I A lek ,x* , he CXX ) * In at Norm ( / t delxtt.NL#x*)t62IH ° ) I ( 4*14=5 o , B b- D C Predictive values new on ' . nu Norm ( O ~ C ) y B CTA " - , Norm ( let XIX ) ( klx ' ) ' 5 ,x)taI ~ hlx.xlt62IThk.x.tl ) k(x*,x* ) ( tix - - yuk ) 5=4 Assume pix In ) practice : o = \
Processes Gaussian Practical View : Generalization Multivariate Normal of i= 1£ Prior ) pitch I ) function blini flu µ on at values finite [ lil :-. In , Em ) set of points m t ' E " - fetal E ( pi Norm E ) . ,FEmD - n , , . . Norml fu 6 ) Yul E. fan , x Can P'5t compute Predictive pcyttly ) linear ← ; = using pig ) algebra
Wr have does OICXIW not Gaussian Processes Interpretation diagonal be i to ( ) Bayesian Ridge Regression Features with N XD DXI Norm ( Norm ( ) Y )Efw ELY ) EI n m , tell ) OI ( Xo ) OIK ] ) mo = = = Cov [ 4 ] Cov I w ] IK ) I 62 t = Covlw ] # I Xlt IN 62 I + = N xD Dxb µ DX kk ④ G) So # HT ,Nt5I 6- I t = = - . - hkh.im ) CENTS , Ym ] fun =¢ dem ) Cov .
OIKIW does have not Gaussian Processes Interpretation be diagonal i to ( ) Bayesian Ridge Regression with Features Norm ( mo , Norm ( Y ) W EI n - , Equivalent Process Gaussian GPG.ucxt.hk.lt ) Norm ( I ) Y FIX ) Fr 62 n , IO ( x ) So KIT kcx OI ,x ) MX ) = mo = kernel Use Computational Advantage trick to : high feat dimensional evaluate products spaces in inner -
Gaussian Ridge Regression Processes us GPC.mx/,hlx.Xl ) Norm ( I ) 4 FIX ) Fr 62 n , 't 14=51 IO ( x ) So # KIT kcx OI ,x ) MX ) CID mo = = to N I ' S Derive Homework this in ; titty :X ) ( let x. x ) 0447=011×9 Ely his = # KIT ( ) # Cx )Ttg÷I5' y Ik Complexity : + III ) " OI Htt ) ( OI KY # OCD ) It Cxlty K ) = Posterior Ridge Regression to equivalent Conclusion : mean
Kennel Regularization Regression - based in 008 ¥1 ⑧ ⑧ Ifl ooo € ① o hi I . 3h55 , Ys ya , be yz9uy5 Small I y* " O I I D= o co i ' 15.1 # y I O Large 0 A # y y* . .de/0eCXm In In In kernel Choice of = § Old ( ) So ht > ) ) implies functor , choice of D e
Kernel Hyper parameters Choosing Rasmussen Carl Source : exp (-1×2*3) h( ' ) Squared Exponential x : x. = - l stronger Large regularization means
kernels Matern Idea functions h times differentiable prior over : Rainforth , Bessel PhD Thesis Tom function Source : - k=Lu - D I 'll ) 6f }l÷ , KfM2q leu ( ' ) E HE ,I 0=312,512 , - = " . - Gamma function
Kernels Basis Duvenaud PhD David Source Thesis : ,
Combinations kernels of Duvenaud PhD David Source Thesis : , ' ) ' ) Sumi ,E I be ,( I. thzk h( In ,I = . ' ) hz( I ,I ' ) Product ,k I be ,( I. hl In : . =
Gaussian Processes Limitations : Limitation Computational I Complexity i NXM µxN FIT .fr/Vonm(k(xIx)lklx.xlto2IYy hlx.xlt62IThk.x.tl ) k(x4x* ) ( lek - NXN NXM MAN MXN Limitation Dimensionality 2 : Rib best Gaussian work when Xue processes ( f with assumptions Intuition smoothness I to D f : dimensionality ) high D because helpful of not curse in
Bayesian Regression Processes Gaussian and Bayesian Regression ( XP f pcfly ) ; = angfmae Ridge MAP estimation regression is - Gaussian with weights prior on variances D= Regularization increases observation with 67 - weight decreases ' noise and with Idf Gaussian Processes ply 'T f) # plfly ) : y r . Provides estimate of uncertainty predictions in - Posterior equivalent is ridge to regression mean - > ) OCD ) complexity vs -
Recommend
More recommend