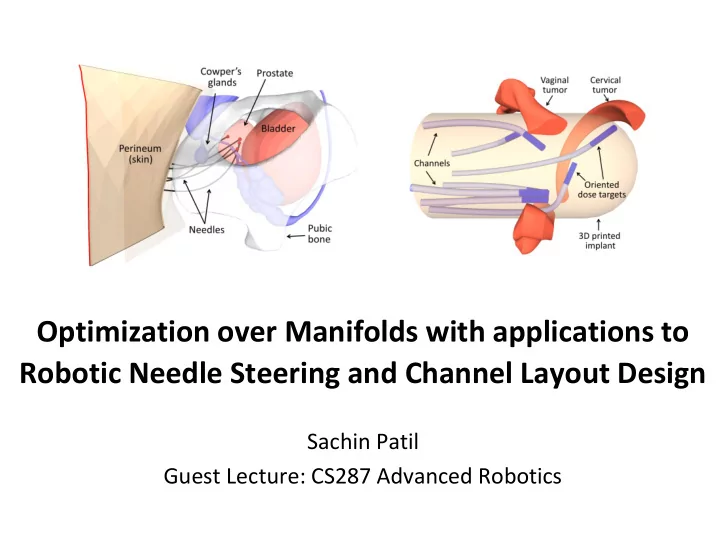
Optimization over Manifolds with applications to Robotic Needle - PowerPoint PPT Presentation

Optimization over Manifolds with applications to Robotic Needle Steering and Channel Layout Design Sachin Patil Guest Lecture: CS287 Advanced Robotics

Trajectory Optimization Optimization over n vector spaces

Not All State- Spaces are ‘Nice’ • Nonholonomic system cannot move in arbitrary directions in its state space 1 : [ , , ]  x y  2 • For a simple car: Configuration space is in (the SE(2) group)

Nonholonomy Examples      2 1 1 Bicycle: 2 1 1 1 Car pulling trailers: Rolling Ball: ?  2 SO (3)

C-Spaces as Manifolds Manifold: Topological space that near each point resembles Euclidean space Other examples:

Optimization over Manifolds n ?

Optimization over Manifolds n

Optimization over Manifolds n Define projection operator from tangent space to manifold

Case Study: Rotation Group (SO(3)) Rotation matrices:  • Unique representation 3 3 • ‘Smooth’ Optimization over SO(3) arises in robotics, graphics, vision etc.

Parameterization: Incremental Rotations  Why not directly optimize over rotation matrix entries?  Over-constrained (orthonormality)  Larger number of optimization variables  Define local parameterization in terms of incremental rotation : Incremental rotation to r reference rotation defined r in terms of axis-angle

Projection Operator e r [ ] : Point on SO(3) that can be reached by traveling along the r geodesic in direction r e r [ ]    0 r r z y    where [ ] r  r 0 r z x    r r 0 y x  1   X k and is the e X k  k 0 matrix exponential operator

Optimization Procedure i ˆ ˆ   1) Seed trajectory: i i [ R , , R ] 1 n 2) Objective subject to: Constraints min i i i   [ , r , r ] 1 n   i 1 ˆ ˆ i i  i [ r ] i [ r ] 3) Compute new trajectory: [ R e · 1 , , R e · n ] 1 n i   1  4) Reset increments: 0 0 [ , , ] r e r [ ]

Steerable Needle Steerable Prostate needle Cowper’s gland Skin Target Bladder Pelvis Steerable needles navigate around Steerable needles inside sensitive structures (simulated) phantom tissue

Steerable Needle Reaction forces from tissue Bevel-tip  3 State (needle tip) SE (3) : SO (3) • Position: 3D • Orientation: 3D Follows constant curvature paths Highly flexible [Webster, Okamura, Cowan, Chirikjian, Goldberg, Alterovitz United States Patent 7,822,458. 2010]

Steerable Needle: Opt Formulation

Steerable Needle Plans

Results Why is minimizing twist important?

Channel Layout (Brachytherapy Implants)

Channel Layout: Opt Formulation

Results

Takeaways  Optimization over manifolds – Generalization of optimization over Euclidean spaces  Define incremental parameterization and projection operators between tangent space and manifold  Optimize over increments; reset after each SQP iteration!

Parameterization: Euler Angles Euler angles What problems do you foresee in directly using Euler angles in optimization?

Parameterization: Euler Angles       Topology not preserved: [0,2 ] [0,2 ] [0,2 ]  Not unique, discontinuous  Gimbal lock

Parameterization: Axis-Angles Orientation defined as rotation around axis • 3-vector; norm of vector is the angle

Parameterization: Axis-Angles Distances are not preserved! Solution: Keep re-centering the axis-angle around a reference rotation (identity)