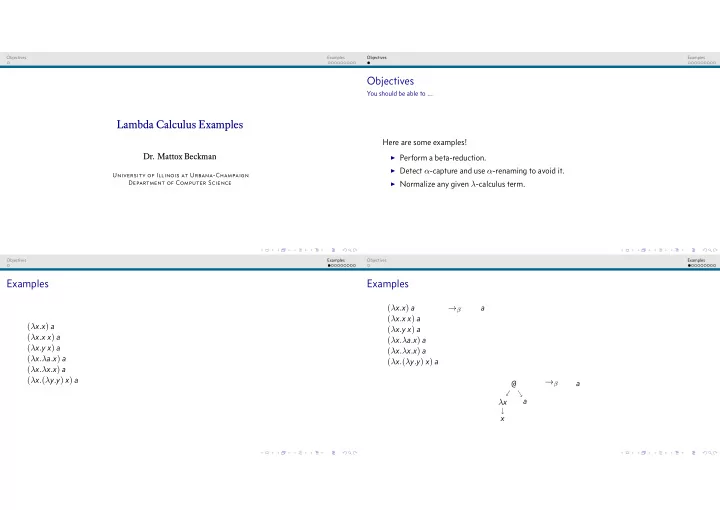
Objectives You should be able to ... Lambda Calculus Examples Here - PowerPoint PPT Presentation

Objectives Examples Objectives Examples Objectives You should be able to ... Lambda Calculus Examples Here are some examples! Dr. Mattox Beckman ◮ Perform a beta-reduction. ◮ Detect α -capture and use α -renaming to avoid it. University of Illinois at Urbana-Champaign ◮ Normalize any given λ -calculus term. Department of Computer Science Objectives Examples Objectives Examples Examples Examples ( λ x . x ) a a → β ( λ x . x x ) a ( λ x . x ) a ( λ x . y x ) a ( λ x . x x ) a ( λ x .λ a . x ) a ( λ x . y x ) a ( λ x .λ x . x ) a ( λ x .λ a . x ) a ( λ x . ( λ y . y ) x ) a ( λ x .λ x . x ) a ( λ x . ( λ y . y ) x ) a a @ → β a λ x x

Objectives Examples Objectives Examples Examples Examples ( λ x . x ) a a ( λ x . x ) a a → β → β ( λ x . x x ) a a a ( λ x . x x ) a a a → β → β ( λ x . y x ) a y a ( λ x . y x ) a → β ( λ x .λ a . x ) a ( λ x .λ a . x ) a ( λ x .λ x . x ) a ( λ x .λ x . x ) a ( λ x . ( λ y . y ) x ) a ( λ x . ( λ y . y ) x ) a → β @ → β @ @ @ y a a a a a λ x λ x @ @ y x x x Objectives Examples Objectives Examples Examples Examples ( λ x . x ) a a ( λ x . x ) a a → β → β ( λ x . x x ) a a a ( λ x . x x ) a a a → β → β ( λ x . y x ) a y a ( λ x . y x ) a y a → β → β ( λ x .λ a . x ) a ( λ x .λ a ′ . x ) λ a ′ . a ( λ x .λ a . x ) a ( λ x .λ a ′ . x ) λ a ′ . a → α → β → α → β ( λ x .λ x . x ) a ( λ x .λ x . x ) a λ x . x → β ( λ x . ( λ y . y ) x ) a ( λ x . ( λ y . y ) x ) a → β @ λ a → α,β @ λ x λ a ′ �→ x a a a a λ x λ x λ x λ a x x

Objectives Examples Objectives Examples Examples Examples ( λ x . x ) a a ( λ x . x ) a a → β → β ( λ x . x x ) a a a ( λ x . x x ) a a a → β → β ( λ x . y x ) a y a ( λ x . y x ) a y a → β → β ( λ x .λ a . x ) a ( λ x .λ a ′ . x ) λ a ′ . a ( λ x .λ a . x ) a ( λ x .λ a ′ . x ) λ a ′ . a → α → β → α → β ( λ x .λ x . x ) a λ x . x ( λ x .λ x . x ) a λ x . x → β → β ( λ x . ( λ y . y ) x ) a ( λ y . y ) a ( λ x . ( λ y . y ) x ) a ( λ y . y ) a → β a → β → β → β → β a → β → β a @ @ @ @ a a λ x λ y a λ x λ y a @ y @ y x x λ y λ y y y Objectives Examples Objectives Examples α capture Here’s One for You to Try! ◮ Convert this tree into an equivalent λ term. ◮ Identify the free variables. ◮ Simplify it by performing as many β reductions (and necessary α renamings) as possible. ( λ x .λ a . x ) a → α ( λ x .λ a ′ . x ) λ a ′ . a → β @ ◮ If a free occurrence of a variable gets placed under a λ that binds it, this is called α @ λ a capture. λ q λ x @ ◮ To resolve this, rename the binder . λ f f a a @ x f

@ f a @ @ q a a f f f f q f a aa Objectives Examples Objectives Examples Solution Solution, Step 1 @ 1 @ @ 1 @ λ a @ 2 λ a @ 2 λ a λ q @ λ q λ x λ x @ 4 λ q λ x @ 4 a a λ f f a a λ f ′ f λ f f a a @ @ 3 @ 3 x f x f x f ′ ( λ xf . fx )( λ q . f )( λ a . aa ) ( λ xf . fx )( λ q . f )( λ a . aa ) ( λ xf ′ . f ′ x )( λ q . f )( λ a . aa ) → α ◮ There is one free variable .... Objectives Examples Objectives Examples Solution, Step 2 Solution, Step 2 @ 1 @ 1 @ 1 λ a λ a λ f ′ λ a @ 2 @ 2 λ q λ q λ x @ 4 λ x @ 4 @ 3 @ 4 a a a a λ q a a λ f ′ f λ f ′ f f ′ f @ 3 @ 3 x x f ′ f ′ ( λ xf ′ . f ′ x )( λ q . f )( λ a . aa ) ( λ xf ′ . f ′ x )( λ q . f )( λ a . aa ) ( λ f ′ . f ′ ( λ q . f ))( λ a . aa ) → β → β

@ q a f @ a a a aa q f @ q q f f q f q f Objectives Examples Objectives Examples Solution, Step 3 Solution, Step 3 @ 1 @ 1 @ 3 λ q λ f ′ λ a λ f ′ λ a λ a @ 3 @ 4 @ 3 @ 4 f @ 4 a a a a a a f ′ λ q f ′ λ q f f ( λ f ′ . f ′ ( λ q . f ))( λ a . aa ) ( λ f ′ . f ′ ( λ q . f ))( λ a . aa ) ( λ a . aa )( λ q . f ) → β → β Objectives Examples Objectives Examples Solution, Step 4 Solution, Step 4 @ 3 @ 3 @ 4 λ q λ q λ q λ q λ a λ a f f f f @ 4 @ 4 a a a a ( λ f ′ . f ′ ( λ q . f ))( λ a . aa ) ( λ f ′ . f ′ ( λ q . f ))( λ a . aa ) ( λ q . f )( λ q . f ) → β → β

f f Objectives Examples Objectives Examples Solution, Step 5 Solution, Step 5 f @ 4 @ 4 λ q λ q λ q λ q f f f f ( λ q . f )( λ q . f ) ( λ q . f )( λ q . f ) f → β → β