( " ' nodes finite set of vertices root . :* :: - PowerPoint PPT Presentation

Oct 11, 2022 •186 likes •219 views

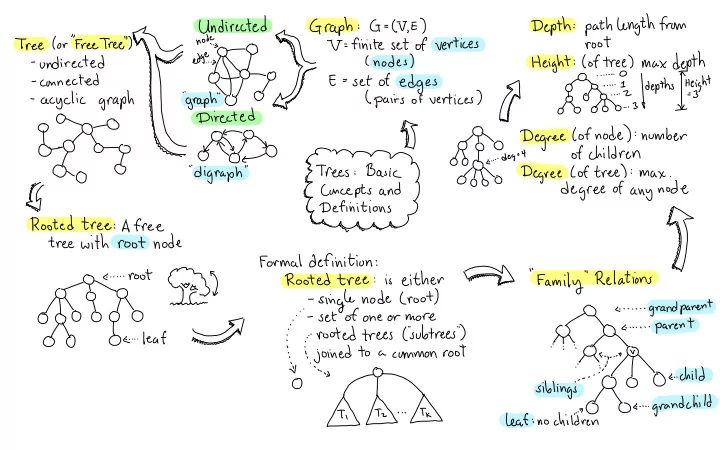
: path length from Depth Graph E) G= : ( " ' nodes finite set of vertices root . :* :: e.ci :* :i . " is ( pairs of vertices ) IF . - acyclic graph " graph " Directed

⇒ : path length from Depth Graph E) G= : ( ÷÷÷÷÷÷÷" ' nodes finite set of vertices root . :* :÷÷÷÷÷÷÷÷÷:÷¥ e.ci :* :i . " is ( pairs of vertices ) IF . - acyclic graph " graph " Directed ← TO %) ° Degree ( of node ) : number ↳ to-do 0 OT , off 't ? ?aegs4 8¥40 of children ftp.g?o:ningw7.68doDesreedkogtrtiee' " o_0 " " digraph ianmgxiode why ' § Rooted " " " To ene .de root 4731 Formal definition : " Relations EDM " " is either Family Rooted tree : - single node ( root ) ta - grandparent 041010610 go a- ' - set of one or more - - - - - ' - parent . ? too . be 0/10 - rooted trees ( : " subtrees " ) ¥ . " " . leaf : . " i. joined to a common root ' : I ' ' i. o ' a. child ( / ) . . 0 . ' sibling 's leaf ; noch ; ¥nb ← - grandchild . "
⇐ ⇐ wasted space ? rooted trees Representing : : A binary tree with Theorem root Each node stores a ( linked ) Eg " . list of its children n nodes has links htt null ③ ⑤ ' ① t.jo?jn%4f.s96 0h Node structure : ' ① ⑤ → next sibling Ff onneodmewe ' " " " " " " first child root £ : " class Btnodegejjodhatra FT In Java : %75inraeenteaetiinmT.in?.tnodese → 7¥d data ; Trees E BTNodehE > left ; > right %Q : ⑧ % lmk why w L u n root : ④ t ⑧ ( not full ) Full : ⇒ go a f " # # called the Binary representation ' ⑦ ⑥ ① ④ ① ⑤ Ye ⑤ Binary tree :D rooted tree t " ' i :& ' " ④ Of ③ 1$ ⑥ of degree 2 , where each " ' Node structure : ' ' ÷ n' Yun two children node has ( possibly null ) lefts right data : Every - leaf node Full non " £7 left ! right has 2 children
m complete Binary Tree : All levels traverse ( Btnodev ) l Traversals How to ( systematically ) visit : full ( except last ) null ) return ; of a rooted tree ? if ( v the nodes ( can be generalized ) visitors - Preorder 09-0 Binary Tree Traversals 2isirsproes@fiIInorderroot.i.gov - process In Innings ;¥÷i÷ Eiichi . . .de . , 4hq" - Lily parental } Challenge : traversals dy so ÷÷÷÷÷÷÷:÷ensimmM TO *d ④ / " n u , _ - a In order : An extended binary atbO*# µ DThm : § ④ tree with n internal nodes Another way to save space . . . Those wasteful null links Threaded binary tree : ( black ) has nil external . . " " " . . . store ( useful ) links in the nodes ( blue ) Q Extended binary ' O null links .( Use a mark bit O %§gQg : Replace IB to distinguish link types Observation : Every tree . ) extended binary tree each null link with E. g. In order Threads : a special leaf node :b BID I 'D Null left - inorder predecessor is full external node Null rights " successor 4

Recommend

Definition ! A (rooted) tree is a structure defined on a finite set of nodes that either: Trees

Definition ! A (rooted) tree is a structure defined on a finite set of nodes that either: Trees Contains no nodes, or Contains a specially designated node called the root and k>=0 disjoint sets of nodes T 1 ,,T k , where

352 views • 3 slides

Intro to graphs Minimum Spanning Trees Graphs nodes/vertices and edges between vertices - set

Intro to graphs Minimum Spanning Trees Graphs nodes/vertices and edges between vertices - set V for vertices, set E for edges - we write graph G = (V ,E) example : cities on a map (nodes) and roads (edges) Adjacency matrix a ij =1 if

980 views • 72 slides

What are Graphs? Nodes and Edges A graph consists of dots called nodes or vertices.

Name _________________ Date _____________ What are Graphs? Nodes and Edges A graph consists of dots called nodes or vertices. There are lines called edges that connect two nodes. Fun activity: Can you trace over all the edges of each

250 views • 5 slides

Finite state automata Finite graphs with labels on edges/nodes Lecture 2 a set of nodes

Finite state automata Finite graphs with labels on edges/nodes Lecture 2 a set of nodes (states) Model-Checking Finite-State Systems a set of edges (transitions) (untimed systems) a set of labels (alphabet) Finite Automata, CTL,

273 views • 10 slides

Model Finite set A of nodes, with partial order . For a, b 2 A , a b

Model Finite set A of nodes, with partial order . For a, b 2 A , a b means b is a downstream node for a . Some nodes are the suppliers of basic inputs, i.e., nodes a such that there is no a 0 a . Some

578 views • 19 slides

Graph Consists of nodes/vertices and edges. Edges may be directed or undirected. Edges

CPSC 3200 Practical Problem Solving University of Lethbridge Graph Consists of nodes/vertices and edges. Edges may be directed or undirected. Edges may be weighted. Representation: adjacency matrix or adjacency list

267 views • 11 slides

61A Lecture 19 Announcements Tree Class Tree Review Nodes Path Root value 3 Values Branch

61A Lecture 19 Announcements Tree Class Tree Review Nodes Path Root value 3 Values Branch 1 2 0 1 1 1 Leaf 0 1 Recursive description (wooden trees): Relative description (family trees): A tree has a root value and a list of

129 views • 10 slides

Graphs (Version of 21 November 2005) Definition: A graph G is a pair ( V, E ), where V is a finite

Graphs (Version of 21 November 2005) Definition: A graph G is a pair ( V, E ), where V is a finite set of items, called the vertices of G , and E is a binary relation on V (that is E V V ); the elements of E connect vertices and

531 views • 11 slides

SEARCH TREE Node: State in state tree Root node: Top of state tree Children: Nodes that can be

AI Lecture. Prof. Carolina Ruiz. Worcester Polytechnic Institute SEARCH TREE Node: State in state tree Root node: Top of state tree Children: Nodes that can be reached from a given node in 1 step (1 operator) Expanding: Generating the children of

335 views • 21 slides

2 6 1 2 3 : black nodes 1 1 1 : red nodes What is the size of the root of the above

Chapter 14: Augmenting Data Structures By augmenting already existing data structures one can build new data structures Augmenting a red-black tree For each node x , add a new field size(x) , the number of non- nil nodes in the subtree rooted at

424 views • 20 slides

SOLVING EQUATIONS IN FINITE ALGEBRAS Erhard Aichinger Institute for Algebra Austrian Science

SOLVING EQUATIONS IN FINITE ALGEBRAS Erhard Aichinger Institute for Algebra Austrian Science Fund FWF P29931 0/37 Using equation solving for: Graph coloring Task: Color the 10 vertices of the graph with 3 colors. d 1 No vertices connected by

963 views • 78 slides

The classification of root systems Maris Ozols University of Waterloo Department of C&O

The classification of root systems Maris Ozols University of Waterloo Department of C&O November 28, 2007 Definition of the root system Definition = R n be a real vector space. A finite subset R E is called Let E root system if

957 views • 60 slides

Tree Searching Tree searches A tree search starts at the A root and explores nodes from

Tree Searching Tree searches A tree search starts at the A root and explores nodes from there, looking for a goal node (a node that satisfies B C certain conditions, depending on the problem) D E F G For some problems, any goal

282 views • 16 slides

Data Setup (Transfer) CPU GPU vertices f0 f1 .. f10 f11 f0 f1 f2 f3 f4 f5 f6 f7 f8

Data Setup (Transfer) CPU GPU vertices f0 f1 .. f10 f11 f0 f1 f2 f3 f4 f5 f6 f7 f8 f9 f10 f11 12 numbers transferred Read mesh on CPU meaning not known GLfloat vertices[12] = { // 12 floats 6 2D vertices? -0.90, -0.90,

134 views • 11 slides

PRESS ROOT TO PRESS ROOT TO CONTINUE: PRESS ROOT TO PRESS ROOT TO CONTINUE: PRESS ROOT TO

Mario Vuksan & Tomislav PericinBlackHat USA 2013, Las Vegas PRESS ROOT TO PRESS ROOT TO CONTINUE: PRESS ROOT TO PRESS ROOT TO CONTINUE: PRESS ROOT TO PRESS ROOT TO PRESS ROOT TO PRESS ROOT TO CONTINUE: CONTINUE: CONTINUE: CONTINUE:

690 views • 45 slides

Certicate Transparency Root Explorer Nikita Korzhitskii Niklas Carlsson Web Public Key

Certicate Transparency Root Explorer Nikita Korzhitskii Niklas Carlsson Web Public Key Infrastructure (WebPKI) Root certificates of trusted Certificate Authorities e.g. GlobalSign Root CA, Amazon Root CA, GoDaddy Root CA Root 1 Root 2

347 views • 19 slides

tree traversal Oct. 25/26, 2017 1 2 Tree Traversal How to visit (enumerate, iterate through,

COMP 250 Lecture 20 tree traversal Oct. 25/26, 2017 1 2 Tree Traversal How to visit (enumerate, iterate through, traverse ) all the nodes of a tree ? 3 depthfirst (root){ // preorder if (root is not empty){ visit root for each

856 views • 49 slides

Slides built from Carter Chapter 4 Vertices Objects are made up of 3D points called vertices.

Slides built from Carter Chapter 4 Vertices Objects are made up of 3D points called vertices. A Vertex is a point in space. In 3D it has 3 coordinates, (X,Y,Z) We can generate vertices, design them, or load them Getting an

770 views • 33 slides

The zeta-function of the root system of type G 2 Kohji Matsumoto (Nagoya University) (a joint

The zeta-function of the root system of type G 2 Kohji Matsumoto (Nagoya University) (a joint work with Y.Komori and H.Tsumura) 1 V : r -dimensional real vector space , : inner product defined on V : finite reduced root system in V

268 views • 24 slides

Scaling the Root A study of the impact on the DNS root system of increasing the size and

Scaling the Root A study of the impact on the DNS root system of increasing the size and volatility of the root zone Jaap Akkerhuis Lyman Chapin Patrik Fltstrm Glenn Kowack Bill Manning Lars-Johan Liman Summary of Findings Root Scaling

558 views • 20 slides

Recursion on Trees 7 January 2019 OSU CSE 1 Structure of Trees Two views of a tree: A

Recursion on Trees 7 January 2019 OSU CSE 1 Structure of Trees Two views of a tree: A tree is made up of: A root node A string of zero or more child nodes of the root, each of which is the root of its own tree A tree is

557 views • 37 slides

Root Cause Analysis 1 Root Cause Analysis Root Cause Analysis is a method that is used to

Root Cause Analysis 1 Root Cause Analysis Root Cause Analysis is a method that is used to address a problem or non-conformance, in order to get to the root cause of the problem. It is used so we can correct or eliminate the cause,

389 views • 28 slides

Graph Representation and Traversals Mark Redekopp David Kempe Sandra Batista 2 GRAPH

1 CSCI 104 Graph Representation and Traversals Mark Redekopp David Kempe Sandra Batista 2 GRAPH REPRESENTATIONS 3 Graph Notation A graph is a collection of vertices h (or nodes) and edges that b c connect vertices a A vertex d

806 views • 26 slides

Definitions Topic 18 Binary Trees A tree is an abstract data type root node internal one entry

Definitions Topic 18 Binary Trees A tree is an abstract data type root node internal one entry point, the root nodes "A tree may grow a Each node is either a leaf or an internal node thousand feet tall, but An internal node has 1 or

286 views • 13 slides