Neutron matter based on chiral effective field theory interactions - - PowerPoint PPT Presentation

SLIDE 1

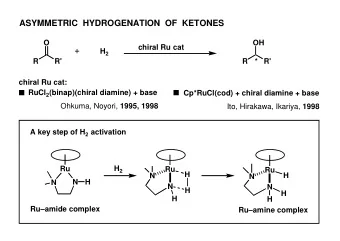
Neutron matter based on chiral effective field theory interactions

Ingo Tews, Technische Universität Darmstadt

Theory Seminar, LANL, April 3, 2014

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 1

SLIDE 2

Main points

• 1. Chiral effective field theory: Epelbaum et al., PPNP (2006) and RMP (2009)

◮ Systematic basis for nuclear forces, naturally includes many-body forces ◮ Very successful in calculations of nuclei and nuclear matter

• 2. Neutron matter calculations with chiral EFT: IT, Krüger, Hebeler, Schwenk, PRL (2013)

◮ Constraints on equation of state ◮ Constraints on astrophysical observables

• 3. Quantum Monte Carlo calculations with chiral EFT interactions

◮ Very precise for strongly interacting systems ◮ Need of local interactions (only depend on r = ri − rj ↔ q) ◮ Several sources of nonlocality in chiral EFT ◮ Can be removed to N2LO

Gezerlis, IT, Epelbaum, Gandolfi, Hebeler, Nogga, Schwenk, PRL (2013)

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 2

SLIDE 3

Motivation

Physics of neutron matter used in a wide variety of applications and density regimes:

• J. Hester (ASU) et al., CXC, HST, NASA

Universal properties at low densities:

◮ Ultracold atoms

Nuclear densities:

◮ Neutron-rich nuclei

Very high densities:

◮ Neutron stars

To understand these phenomena → better understanding of neutron matter

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 3

SLIDE 4

Motivation

• J. Hester (ASU) et al., CXC, HST, NASA

For model equations of state:

◮ Pressure is correlated with

neutron star radius

◮ Pressure variation by a factor

• f 6 at saturation density

(unrealistic) Hebeler, Lattimer,

Pethick, Schwenk, PRL (2010)

⇒ Sizeable radius range for

neutron stars

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 4

SLIDE 5

Motivation

8 10 12 14 16

Radius [km]

0.5 1 1.5 2 2.5 3

Mass [M°

.]

causality

For model equations of state:

◮ Pressure is correlated with

neutron star radius

◮ Pressure variation by a factor

• f 6 at saturation density

(unrealistic) Hebeler, Lattimer,

Pethick, Schwenk, PRL (2010)

⇒ Sizeable radius range for

neutron stars

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 4

SLIDE 6

Chiral Effective Field Theory for Nuclear Forces

Basic principle of effective field theory:

u d d u d d u d d

R λ≫R

At low energies (long wavelength) details not resolved!

◮ Choose relevant degrees of freedom for low-energy processes ◮ Systematic expansion of interaction terms constrained by symmetries

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 5

SLIDE 7

Chiral effective field theory for nuclear forces

Separation of scales: low momenta q ≪ breakdown scale ΛB Write most general Lagrangian and expand in powers of (q/ΛB)n n=0: leading order (LO), n=2: next-to-leading order (NLO), ... expansion parameter ≈ 1/3 Systematic: can work to desired accuracy and obtain error estimates

Weinberg, van Kolck, Kaplan, Savage, Wise, Epelbaum, Hammer, Kaiser, Machleidt, Meißner,...

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 6

SLIDE 8

Chiral effective field theory for nuclear forces

❞ ❡ ❞ ❡ ❞ ❡ ❞ ❡

Explicit degrees of freedom: pions and nucleons Long-range physics explicit, short-range physics expanded in general operator basis High-momentum physics absorbed into short-range couplings, fit to experiment

Weinberg, van Kolck, Kaplan, Savage, Wise, Epelbaum, Hammer, Kaiser, Machleidt, Meißner,...

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 7

SLIDE 9

Chiral effective field theory for nuclear forces

❞ ❡ ❞ ❡ ❞ ❡ ❞ ❡ ❞ ❡ ❞ ❡ ❞ ❡ ✏ ✏ ✮ ✏ ✏ ✶

Many-body forces are crucial Consistent interactions: same couplings for NN and many-body sector

Weinberg, van Kolck, Kaplan, Savage, Wise, Epelbaum, Hammer, Kaiser, Machleidt, Meißner,...

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 8

SLIDE 10

Chiral effective field theory for nuclear forces

❞ ❡ ❞ ❡ ❞ ❡ ❞ ❡ ❞ ❡ ❞ ❡ ✏ ✏ ✮ ✏ ✏ ✶

Many-body forces are crucial Consistent interactions: same couplings for NN and many-body sector In many calculations

• nly

N2LO 3N forces included

Weinberg, van Kolck, Kaplan, Savage, Wise, Epelbaum, Hammer, Kaiser, Machleidt, Meissner,...

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 9

SLIDE 11

3N Interactions at N2LO

3N forces: only two new couplings:

Hebeler et al., PRC (2010)

✐ ❥ ❦ ✐ ❥ ❦

cD and cE terms vanish in neutron matter for symmetric regulator

→ neutron matter exciting lab system

Only long-range two-pion exchange contributes for neutrons, depends on c1 and c3: Krebs et al., PRC (2012) N2LO: c1 = −(0.37 − 0.81) GeV−1 and c3 = −(2.71 − 3.40) GeV−1 N3LO: c1 = −(0.75 − 1.13) GeV−1 and c3 = −(4.77 − 5.51) GeV−1

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 10

SLIDE 12

Impact of 3N forces - neutron-rich nuclei

Shell model: Otsuka et al., PRL (2010)

NN + 3N forces: give correct physics of neutron-rich nuclei (oxygen dripline)

see also Hagen et al., PRL (2012), Hergert et al., PRL (2013)

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 11

SLIDE 13

Impact of 3N forces - nuclear matter

Chiral EFT constrains nuclear-matter energy per particle

MBPT: Hebeler et al., PRC (2011)

Couplings cD and cE fitted to

3H and 4He properties

NN + 3N forces: give correct saturation with theoretical uncertainties for symmetric nuclear matter

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 12

SLIDE 14

Impact of 3N forces - neutron matter

MBPT: Hebeler et al., PRC (2010)

NN + 3N forces: Uncertainties in many-body forces larger than many-body calculational uncertainties!

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 13

SLIDE 15

Chiral effective field theory for nuclear forces

❞ ❡ ❞ ❡ ❞ ❡ ❞ ❡ ❞ ❡ ❞ ❡ ✏ ✏ ✮ ✏ ✏ ✶

Recently: first complete N3LO neutron matter calculation

IT, Krüger, Hebeler, Schwenk, PRL 2013

In neutron matter:

◮ simpler, only certain parts of the

many-body forces contribute

◮ chiral 3- and 4-neutron forces are

predicted to N3LO

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 14

SLIDE 16

3N Interactions at N3LO

11 8(−1 + z)(1 + z)M 4

π

• 3zq3

1 +

• −1 + 10z2

q2

1q3 + 3z

• 1 + 2z2

q1q2

3 +

• 1 + 2z2

q3

3

• +

2M 2

πq2 2

• z
• −3 + z2

q3

1 +

• 3 − 9z2

q2

1q3 − z

• 5 + z2

q1q2

3 +

• −3 − 3z2 + 4z4

q3

3

• +

zg6

AMπ

• 2M 2

π + q2 3

q2

2q3 + 4M 2 π (zq1 + q3)

• 128F 6πq1 (−4 (−1 + z2) M 2

π + q2 2) q2 3 (4M 2 π + q2 3) ,

R4 = A (q2) g6

Aq2 2

• −2z2q2

1q3 +

• 1 + z2

q3

3 + 2M 2 π

• 2zq1 +
• 1 + z2

q3

• 128F 6π (−1 + z2)2 q2

1q3 3

+ A (q1) g6

A

• −2M 2

π

• 2zq2

1 +

• 1 + 3z2

q1q3 + 2zq2

3

• + q3
• 2z2q3

1 + 2z3q2 1q3 +

• 1 − 4z2 + z4

q1q2

3 − 2zq3 3

• 128F 6π (−1 + z2)2 q1q3

3

− A (q3) g6

A

128F 6π (−1 + z2)2 q2

1q2 3

• 2M 2

π

• −z2

−3 + z2 q2

1 + z

• 3 + z2

q1q3 +

• 1 + z2

q2

3

• +

q3

• −
• z + z3

q3

1 −

• 1 − z2 + 2z4

q2

1q3 + z

• 1 + z2

q1q2

3 +

• 1 + z2

q3

3

• −

I(4 : 0, −q1, q3; 0)g6

A

32F 6 (−1 + z2)2 q1 (−4 (−1 + z2) M 2

π + q2 2) q2 3

• q4

2q3

• z + z3

q2

1 +

• −1 + z22 q1q3 − 2zq2

3

• +

8(−1 + z)(1 + z)M 4

π

• 3z2q3

1 + 9z3q2 1q3 +

• −2 + 9z2 + 2z4

q1q2

3 + z

• 2 + z2

q3

3

• +

2M 2

πq2 2

• z2

−3 + z2 q3

1 +

• 2z − 8z3

q2

1q3 +

• 4 + 5z2

−3 + z2 q1q2

3 + 2z

• −3 + z2 + z4

q3

3

• +

zg6

AMπ

• 2M 2

π + q2 3

q2

2q3 + 4M 2 π (zq1 + q3)

• 128F 6πq1 (−4 (−1 + z2) M 2

π + q2 2) q2 3 (4M 2 π + q2 3) ,

R5 = A (q2) g6

Aq2 2

• −4M 2

π (q1 + zq3) + q3

• 2zq2

1 +

• −1 + z2

q1q3 − 2zq2

3

• 128F 6π (−1 + z2)2 q1q4

3

− A (q3) g6

A

128F 6π (−1 + z2)2 q1q3

3

• 2M 2

π

• z
• −3 + z2

q2

1 − 2

• 1 + z2

q1q3 − 2zq2

3

• + q3
• 1 + z2

q3

1 + 2z3q2 1q3−

• 1 + z2

q1q2

3 − 2zq3 3

• +

A (q1) g6

A

• 2M 2

π

• 2q2

1 + 4zq1q3 +

• 1 + z2

q2

3

• + q3
• −2zq3

1 +

• 1 − 3z2

q2

1q3 + 2zq1q2 3 +

• 1 + z2

q3

3

• 128F 6π (−1 + z2)2 q4

3

+ I(4 : 0, −q1, q3; 0)g6

A

32F 6 (−1 + z2)2 (−4 (−1 + z2) M 2

π + q2 2) q3 3

• q4

2q3

• 1 + z2

q2

1 + z

• −1 + z2

q1q3 −

• 1 + z2

q2

3

• +

8(−1 + z)(1 + z)M 4

π

• 3zq3

1 +

• −1 + 10z2

q2

1q3 + 3z

• 1 + 2z2

q1q2

3 +

• 1 + 2z2

q3

3

• +

2M 2

πq2 2

• z
• −3 + z2

q3

1 +

• 3 − 9z2

q2

1q3 − z

• 5 + z2

q1q2

3 +

• −3 − 3z2 + 4z4

q3

3

• −

g6

AMπ

• 2M 2

π + q2 3

q2

2q3 + 4M 2 π (zq1 + q3)

• 128F 6π (−4 (−1 + z2) M 2

π + q2 2) q3 3 (4M 2 π + q2 3) ,

R6 = A (q2) g6

A

• 2M 2

π + q2 2

• 128F 6π

+ A (q1) g6

A

• 2z
• M 2

π + q2 1

• q3 + q1
• 8M 2

π + 3q2 1 + q2 3

• 128F 6πq1

+ A (q3) g6

A

• 2zq1
• M 2

π + q2 3

• + q3
• 8M 2

π + q2 1 + 3q2 3

• 128F 6πq3

− g6

AMπ

128F 6πq1 (4M 2

π + q2 1) (4 (−1 + z2) M 2 π − q2 2) q3 (4M 2 π + q2 3)

• 5 + z2

q3

1q2 2q3 3 + 8M 6 π

• z
• −3 + 4z2

q2

1+

2

• 19 − 18z2

q1q3 + z

• −3 + 4z2

q2

3

• + 2M 4

π

• 4z
• −1 + z2

q4

1 +

• 77 − 36z2

q3

1q3 + 2z

• 33 + 8z2

q2

1q2 3+

• 77 − 36z2

q1q3

3 + 4z

• −1 + z2

q4

3

• + 2M 2

πq1q3

• 10 + z2

q4

1 + 2z

• 9 + 2z2

q3

1q3 +

• 29 − 7z2

q2

1q2 3+

2z

• 9 + 2z2

q1q3

3 +

• 10 + z2

q4

3

• −

I(4 : 0, −q1, q3; 0)g6

A

• 2M 2

π + q2 2

• 32F 6q1 (−4 (−1 + z2) M 2

π + q2 2) q3

• q1q2

2q3

• q2

1 + zq1q3 + q2 3

• + 4M 4

π

• zq2

1 − 2

• −2 + z2

q1q3 + zq2

3

• +

2M 2

π

• 4q1q3
• q2

1 + q2 3

• + z
• q4

1 + 6q2 1q2 3 + q4 3

• ,

12 R7 = 3g6

AMπ

• 2M 2

π + q2 2

• 256F 6πq2

1 (−4 (−1 + z2) M 2 π + q2 2) − 3A (q3) g6 A

• 2M 2

π + q2 2

1 + z2 q1 + 2zq3

• 256F 6π (−1 + z2)2 q3

1

− 3A (q1) g6

A

• 2M 2

π + q2 2

2zq1 +

• 1 + z2

q3

• 256F 6π (−1 + z2)2 q2

1q3

+ 3A (q2) g6

A

• 2M 2

π + q2 2

2zq2

1 +

• 1 + 3z2

q1q3 + 2zq2

3

• 256F 6π (−1 + z2)2 q3

1q3

+ 3I(4 : 0, −q1, q3; 0)g6

A

• 2M 2

π + q2 2

• 64F 6 (−1 + z2)2 q2

1 (4 (−1 + z2) M 2 π − q2 2)

• −q2

2

• 1 + z2

q2

1 + z

• 3 + z2

q1q3 +

• 1 + z2

q2

3

• +

4

• −1 + z2

M 2

π

• 1 + 2z2

q2

1 + 2z

• 2 + z2

q1q3 +

• 1 + 2z2

q2

3

• ,

R8 = − 3zg6

AMπ

• 2M 2

π + q2 2

• 256F 6πq1 (−4 (−1 + z2) M 2

π + q2 2) q3

+ 3zA (q3) g6

A

• 2M 2

π + q2 2

1 + z2 q1 + 2zq3

• 256F 6π (−1 + z2)2 q2

1q3

+ 3zA (q1) g6

A

• 2M 2

π + q2 2

2zq1 +

• 1 + z2

q3

• 256F 6π (−1 + z2)2 q1q2

3

− 3zA (q2) g6

A

• 2M 2

π + q2 2

2zq2

1 +

• 1 + 3z2

q1q3 + 2zq2

3

• 256F 6π (−1 + z2)2 q2

1q2 3

− 3I(4 : 0, −q1, q3; 0)zg6

A

• 2M 2

π + q2 2

• 64F 6 (−1 + z2)2 q1 (4 (−1 + z2) M 2

π − q2 2) q3

• −q2

2

• 1 + z2

q2

1 + z

• 3 + z2

q1q3 +

• 1 + z2

q2

3

• +

4

• −1 + z2

M 2

π

• 1 + 2z2

q2

1 + 2z

• 2 + z2

q1q3 +

• 1 + 2z2

q2

3

• ,

R9 = −3A (q2) g6

A

• 2M 2

π + q2 2

1 + z2 q2

1 + z

• 3 + z2

q1q3 +

• 1 + z2

q2

3

• 256F 6π (−1 + z2)2 q2

1q2 3

+ 3A (q1) g6

A

• 1 + z2

q3

1 + 2z

• 2 + z2

q2

1q3 − z2

−7 + z2 q1q2

3 + 2zq3 3 + 2M 2 π

• 1 + z2

q1 + 2zq3

• 256F 6π (−1 + z2)2 q1q2

3

+ 3A (q3) g6

A

• 2zq3

1 − z2

−7 + z2 q2

1q3 + 2z

• 2 + z2

q1q2

3 +

• 1 + z2

q3

3 + 2M 2 π

• 2zq1 +
• 1 + z2

q3

• 256F 6π (−1 + z2)2 q2

1q3

+ 3I(4 : 0, −q1, q3; 0)zg6

A

• 2M 2

π + q2 2

• 64F 6 (−1 + z2)2 q1 (−4 (−1 + z2) M 2

π + q2 2) q3

• q2

2

• −2q2

1 + z

• −5 + z2

q1q3 − 2q2

3

• +

4

• −1 + z2

M 2

π

• 2 + z2

q2

1 + 6zq1q3 +

• 2 + z2

q2

3

• −

3zg6

AMπ

• 2M 2

π + q2 2

• 256F 6πq1 (−4 (−1 + z2) M 2

π + q2 2) q3

, R10 = 3

• −1 + z2

g6

AMπ

• 2M 2

π + q2 2

• 256F 6π (−4 (−1 + z2) M 2

π + q2 2) + 3A (q2) g6 A

• 2M 2

π + q2 2

• (zq1 + q3) (q1 + zq3)

256F 6π (−1 + z2) q1q3 − 3A (q1) g6

A

• zq3

1 +

• 1 + 2z2

q2

1q3 − z

• −4 + z2

q1q2

3 + q3 3 + 2M 2 π (zq1 + q3)

• 256F 6π (−1 + z2) q3

− 3A (q3) g6

A

• q3

1 − z

• −4 + z2

q2

1q3 +

• 1 + 2z2

q1q2

3 + zq3 3 + 2M 2 π (q1 + zq3)

• 256F 6π (−1 + z2) q1

+ 3I(4 : 0, −q1, q3; 0)g6

A

• 2M 2

π + q2 2

• 64F 6 (−1 + z2) (4 (−1 + z2) M 2

π − q2 2)

• −q2

2

• q2

1 − z

• −3 + z2

q1q3 + q2

3

• +

4

• −1 + z2

M 2

π

• 1 + z2

q2

1 + 4zq1q3 +

• 1 + z2

q2

3

• ,

R11 = −A (q2) g6

Aq2 2

• 4M 2

π + q2 1 + q2 3

• 256F 6π (−1 + z2) q2

1q2 3

+ A (q3) g6

A

• 2M 2

π

• −1 + z2

q2

1 + 2zq1q3 + 2q2 3

• + q3
• zq3

1 +

• −1 + 2z2

q2

1q3 + zq1q2 3 + q3 3

• 256F 6π (−1 + z2) q2

1q2 3

+ A (q1) g6

A

• 2M 2

π

• 2q2

1 + 2zq1q3 +

• −1 + z2

q2

3

• + q1
• q3

1 + zq2 1q3 +

• −1 + 2z2

q1q2

3 + zq3 3

• 256F 6π (−1 + z2) q2

1q2 3

− I(4 : 0, −q1, q3; 0)g6

Aq2 2

(64F 6 (−1 + z2) q2

1 (−4 (−1 + z2) M 2 π + q2 2) q2 3)

• −
• 2M 2

π + q2 1

2M 2

π + q2 3

4M 2

π + q2 1 + q2 3

• +

2z3q1q3

• −4M 4

π + q2 1q2 3

• + z2

4M 2

π + q2 1 + q2 3

4M 4

π + 3q2 1q2 3 + 2M 2 π

• q2

1 + q2 3

• +

zq1q3

• 8M 4

π + q4 1 + q4 3 + 4M 2 π

• q2

1 + q2 3

• −

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 15

SLIDE 17

3N Interactions at N3LO

2π exchange 2π-1π exchange pion ring (involved) 1π-exchange contact (vanishes) 2π-exchange contact (2-body-contact CT )

Bernard et al., PRC (2008) & PRC (2011)

+relativistic corrections (2-body-contacts CT , CS)

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 16

SLIDE 18

4N Interactions at N3LO

Epelbaum, PLB (2006)

Less involved than 3N forces (no loops) In neutron matter only three diagrams contribute due to isospin structure 4N forces provide small contributions

Fiorilla et al., NPA (2012) Kaiser, EPJ A (2012) McManus, Riska, PLB (1980)

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 17

SLIDE 19

Energy per Particle in Hartree-Fock Approximation

Hartree-Fock is a very good approximation for the energy per particle for 3N forces at N2LO [Hebeler et al., PRC (2010)] Expected to be even better at higher orders! E N = 1

ρn!trσ1· · · trσn d3k1

(2π)3 · · ·

d3kn

(2π)3 f 2

Rnk1 · · · nkn

× 1 · · · n | An

• i1=...=in

V(i1, ... , in) | 1 · · · n all exchange terms included fR = exp

• −

k2

1 + ... + k2 n + k1 · k2 + ... + kn−1 · kn

nΛ2

R

nexp

, nexp = 4 cutoff variation: ΛR = (2 − 2.5) fm−1

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 18

SLIDE 20

Individual N3LO many-body contributions

• 4
• 2

2 4 E/N [MeV]

• 4
• 2

2 4 0.05 0.1 0.15 n [fm-3]

• 0.4
• 0.3
• 0.2
• 0.1

0.1 0.2 0.3 0.4 E/N [MeV] 0.05 0.1 0.15 n [fm-3] 0.05 0.1 0.15 n [fm-3] 0.05 0.1 0.15 0.2 n [fm-3]

• 0.4
• 0.3
• 0.2
• 0.1

0.1 0.2 0.3 0.4

IT, Krüger, Hebeler, Schwenk, PRL (2013)

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 19

SLIDE 21

Individual N3LO many-body contributions

• 4
• 2

2 4 E/N [MeV]

• 4
• 2

2 4

Expected size

0.05 0.1 0.15 n [fm-3]

• 0.4
• 0.3
• 0.2
• 0.1

0.1 0.2 0.3 0.4 E/N [MeV] 0.05 0.1 0.15 n [fm-3] 0.05 0.1 0.15 n [fm-3] 0.05 0.1 0.15 0.2 n [fm-3]

• 0.4
• 0.3
• 0.2
• 0.1

0.1 0.2 0.3 0.4

IT, Krüger, Hebeler, Schwenk, PRL (2013)

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 19

SLIDE 22

Individual N3LO many-body contributions

• 4
• 2

2 4 E/N [MeV]

• 4
• 2

2 4 EM 500 MeV EGM 450/700 MeV EGM 450/500 MeV

Expected size

0.05 0.1 0.15 n [fm-3]

• 0.4
• 0.3
• 0.2
• 0.1

0.1 0.2 0.3 0.4 E/N [MeV] 0.05 0.1 0.15 n [fm-3] 0.05 0.1 0.15 n [fm-3] 0.05 0.1 0.15 0.2 n [fm-3]

• 0.4
• 0.3
• 0.2
• 0.1

0.1 0.2 0.3 0.4

IT, Krüger, Hebeler, Schwenk, PRL (2013)

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 19

SLIDE 23

Individual N3LO many-body contributions

• 4
• 2

2 4 E/N [MeV]

• 4
• 2

2 4 EM 500 MeV EGM 450/700 MeV EGM 450/500 MeV

Expected size Large due to ∆ contributions shifted to N4LO

0.05 0.1 0.15 n [fm-3]

• 0.4
• 0.3
• 0.2
• 0.1

0.1 0.2 0.3 0.4 E/N [MeV] 0.05 0.1 0.15 n [fm-3] 0.05 0.1 0.15 n [fm-3] 0.05 0.1 0.15 0.2 n [fm-3]

• 0.4
• 0.3
• 0.2
• 0.1

0.1 0.2 0.3 0.4

IT, Krüger, Hebeler, Schwenk, PRL (2013)

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 19

SLIDE 24

Individual N3LO many-body contributions

• 4
• 2

2 4 E/N [MeV]

• 4
• 2

2 4 EM 500 MeV EGM 450/700 MeV EGM 450/500 MeV

Expected size Large due to ∆ contributions shifted to N4LO

0.05 0.1 0.15 n [fm-3]

• 0.4
• 0.3
• 0.2
• 0.1

0.1 0.2 0.3 0.4 E/N [MeV] 0.05 0.1 0.15 n [fm-3] 0.05 0.1 0.15 n [fm-3] 0.05 0.1 0.15 0.2 n [fm-3]

• 0.4
• 0.3
• 0.2
• 0.1

0.1 0.2 0.3 0.4 EGM 450/500 MeV EGM 450/700 MeV EM 500 MeV relativistic corrections 3N

IT, Krüger, Hebeler, Schwenk, PRL (2013)

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 19

SLIDE 25

Individual N3LO many-body contributions

• 4
• 2

2 4 E/N [MeV]

• 4
• 2

2 4 EM 500 MeV EGM 450/700 MeV EGM 450/500 MeV

Expected size Large due to ∆ contributions shifted to N4LO

0.05 0.1 0.15 n [fm-3]

• 0.4
• 0.3
• 0.2
• 0.1

0.1 0.2 0.3 0.4 E/N [MeV] 0.05 0.1 0.15 n [fm-3] 0.05 0.1 0.15 n [fm-3] 0.05 0.1 0.15 0.2 n [fm-3]

• 0.4
• 0.3
• 0.2
• 0.1

0.1 0.2 0.3 0.4 EGM 450/500 MeV EGM 450/700 MeV EM 500 MeV rel corrections 3N

small IT, Krüger, Hebeler, Schwenk, PRL (2013)

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 19

SLIDE 26

Individual N3LO many-body contributions

• 4
• 2

2 4 E/N [MeV]

• 4
• 2

2 4 EM 500 MeV EGM 450/700 MeV EGM 450/500 MeV

Expected size Large due to ∆ contributions shifted to N4LO

0.05 0.1 0.15 n [fm-3]

• 0.4
• 0.3
• 0.2
• 0.1

0.1 0.2 0.3 0.4 E/N [MeV] 0.05 0.1 0.15 n [fm-3] 0.05 0.1 0.15 n [fm-3] 0.05 0.1 0.15 0.2 n [fm-3]

• 0.4
• 0.3
• 0.2
• 0.1

0.1 0.2 0.3 0.4 EGM 450/500 MeV EGM 450/700 MeV EM 500 MeV rel corrections 3N

small IT, Krüger, Hebeler, Schwenk, PRL (2013)

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 19

SLIDE 27

Individual N3LO many-body contributions

• 4
• 2

2 4 E/N [MeV]

• 4
• 2

2 4 EM 500 MeV EGM 450/700 MeV EGM 450/500 MeV

Expected size Large due to ∆ contributions shifted to N4LO

0.05 0.1 0.15 n [fm-3]

• 0.4
• 0.3
• 0.2
• 0.1

0.1 0.2 0.3 0.4 E/N [MeV] 0.05 0.1 0.15 n [fm-3] 0.05 0.1 0.15 n [fm-3] 0.05 0.1 0.15 0.2 n [fm-3]

• 0.4
• 0.3
• 0.2
• 0.1

0.1 0.2 0.3 0.4 EGM 450/500 MeV EGM 450/700 MeV EM 500 MeV rel corrections 3N

small small + cancellations IT, Krüger, Hebeler, Schwenk, PRL (2013)

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 19

SLIDE 28

Results: Individual 3N Contributions

3N N3LO result at n0:

−(3.2 − 4.8) MeV/N for EGM potentials −0.5 MeV/N for EM potential

0.05 0.1 0.15

n [fm-3]

• 4
• 2

2 4 6 8 10

N2LO 3N (small ci)

0.05 0.1 0.15

n [fm-3]

• 4
• 2

2 4 6 8 10

E/N [MeV] N2LO 3N (large ci)

0.05 0.1 0.15

n [fm-3]

EM 500 MeV EGM 450/700 MeV EGM 450/500 MeV

p N3LO 3N p

0.05 0.1 0.15

n [fm-3]

EM 500 MeV EGM 450/700 MeV EGM 450/500 MeV

Total 3N (large ci)

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 20

SLIDE 29

Comparison: 4N Results with Fiorilla et al.

◮ 4NF in neutron matter

studied by Fiorilla et al.

◮ but only last two diagrams:

E N (ρ0) = −16.2 keV

◮ all topologies:

E N (ρ0) = −174 ± 10 keV

[S. Fiorilla, N. Kaiser, W. Weise, Nucl. Phys. A 880, 65 (2012)]

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 21

SLIDE 30

Chiral EFT for neutron matter

0.05 0.1 0.15

n [fm-3]

5 10 15 20

E/N [MeV]

EM 500 MeV (NN only) EGM 450/500 MeV (NN only) EGM 450/700 MeV (NN only)

NN forces only:

◮ uncertainties due to

many-body calculation small

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 22

SLIDE 31

Chiral EFT for neutron matter

0.05 0.1 0.15

n [fm-3]

5 10 15 20

E/N [MeV]

EM 500 MeV EGM 450/500 MeV EGM 450/700 MeV

NN forces only:

◮ uncertainties due to

many-body calculation small Many-body forces:

◮ have large impact on

neutron-matter energy

◮ uncertainties dominated by

3N forces (large c3)

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 22

SLIDE 32

Chiral EFT for neutron matter

0.05 0.1 0.15

n [fm-3]

5 10 15 20

E/N [MeV]

EM 500 MeV EGM 450/500 MeV EGM 450/700 MeV

Bands include:

◮ Λ = (2 − 2.5) fm−1 ◮ many-body uncertainties ◮ c1 = −(0.75 − 1.13) GeV−1

c3 = −(4.77 − 5.51) GeV−1

Krebs et al., PRC (2012)

Final N3LO result: E N (n0) = (14.1 − 21.0) MeV

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 23

SLIDE 33

Chiral EFT for neutron matter

0.05 0.1 0.15

n [fm-3]

5 10 15 20

E/N [MeV]

EM 500 MeV EGM 450/500 MeV EGM 450/700 MeV NLO lattice (2009) QMC (2010) APR (1998) GCR (2012)

Universal properties at low densities

◮ agreement with

Quantum Monte Carlo and NLO lattice calculations

Gezerlis, Carlson, PRC (2010) Epelbaum et al., EPJ A (2009)

Good agreement with other calculations at higher densities

◮ but in those

no theoretical uncertainties

Akmal et al., PRC (1998) Gandolfi et al., PRC (2012)

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 23

SLIDE 34

From N2LO to N3LO

0.05 0.1 0.15

n [fm-3]

5 10 15 20

E/N [MeV]

N2LO N3LO (only EGM) ◮ Final N2LO result:

E N (n0) = (15.5 − 21.4) MeV

◮ Final N3LO result (EGM only):

E N (n0) = (14.1 − 18.4) MeV

◮ E/N reduced from N2LO to N3LO ◮ Theoretical uncertainty reduced

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 24

SLIDE 35

Chiral EFT for neutron matter

0.05 0.1 0.15

n [fm-3]

5 10 15 20

E/N [MeV]

this work LS 180 LS 220 LS 375 FSU2.1 NL3 TM1 DD2 SFHo SFHx

Chiral EFT constrains neutron-matter energy per particle N3LO many-body forces add more density dependence Rules out many model equations of state

Lines from Hempel, Lattimer, G. Shen

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 25

SLIDE 36

Impact on Symmetry Energy

28 30 32 34 36

SV [MeV]

20 40 60 80

L [MeV]

Tamii et al. (2011) Hebeler et al. (2010) N3LO (this work) Kortelainen et al. (2010)

Neutron matter band puts constraints

• n symmetry energy and its

density dependence

Hebeler et al., PRL (2010)

◮ SV = 28.9 − 34.9 MeV ◮ L = 43.0 − 66.6 MeV

Good agreement with experimental constraints

Dipole polarizability - Tamii et al., PRL (2011) Nuclear masses - Kortelainen et al., PRC (2010)

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 26

SLIDE 37

Impact on Neutron Stars

Equation of state for neutron star matter: extend results to small Ye,p

Hebeler et al., PRL (2010) and APJ (2013)

Agrees with standard crust EOS after inclusion of many-body forces

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 27

SLIDE 38

Impact on Neutron Stars

Equation of state for neutron star matter: extend results to small Ye,p

Hebeler et al., PRL (2010) and APJ (2013)

Agrees with standard crust EOS after inclusion of many-body forces

13.0 13.5 14.0 log 10 [g / cm3] 31 32 33 34 35 36 37 log 10 P [dyne / cm2]

1 2 3

with ci uncertainties

crust

crust EOS (BPS) neutron star matter

12 23 1

Extend to higher densities using polytropic expansion

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 27

SLIDE 39

Impact on Neutron Stars

Nature (2010)

MPSR = 2.01M⊙

Science (2013)

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 28

SLIDE 40

Impact on Neutron Stars

Constrain resulting EOS: causality and observed 1.97 M⊙ neutron star Chiral EFT interactions provide strong constraints for EOS Rule out many model equations of state

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 29

SLIDE 41

Impact on Neutron Stars

8 10 12 14 16

Radius [km]

0.5 1 1.5 2 2.5 3

Mass [M°

.]

this work RG evolved

causality

Radius for 1.4 M⊙ neutron star:

◮ R = 9.7 − 13.9 km

Maximum mass neutron star:

◮ Mmax ≤ 3.05M⊙ (14km)

Uncertainties from many-body forces and polytropic expansion

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 30

SLIDE 42

Impact on Neutron Stars

If a 2.4 M⊙ neutron star was observed: Even stronger constraints on high-density equation of state

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 31

SLIDE 43

Impact on Neutron Stars

8 10 12 14 16

Radius [km]

0.5 1 1.5 2 2.5 3

Mass [M0

.]

this work

causality

Radius for 1.4 M⊙ neutron star:

◮ R = 11.5 − 13.9 km

Maximum mass neutron star:

◮ Mmax ≤ 3.05M⊙ (14km)

Uncertainties from many-body forces and polytropic expansion

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 32

SLIDE 44

Chiral condensate

Chiral condensate is order parameter for chiral phase transition

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 33

SLIDE 45

Chiral condensate

0.05 0.1 0.15 0.2

n [fm-3]

0.6 0.7 0.8 0.9 1

<q _q>n ____ <q _q>0 EGM 450/700 MeV EGM 450/500 MeV leading term ΣπN

Include:

◮ Explicit mπ variation ◮ No mπ-dependent contacts

Constraints on chiral condensate:

[W. Weise, Prog. Part. Nucl. Phys. (2012)]

◮ EGM 450/500: 66.8-69.3% at n0 ◮ EGM 450/700: 67.2-68.9% at n0

Without interaction:

◮ 62.3% at n0

Krüger, IT,Hebeler, Friman, Schwenk, PLB (2013)

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 34

SLIDE 46

Chiral EFT for neutron matter

0.05 0.1 0.15

n [fm-3]

5 10 15 20

E/N [MeV]

this work LS 180 LS 220 LS 375 FSU2.1 NL3 TM1 DD2 SFHo SFHx

Neutron matter from chiral EFT:

◮ chiral EFT constrains

neutron matter equation of state and astrophysical observables

Krüger, IT, Hebeler, Schwenk, PRC (2013)

So far used in perturbative calculations

◮ need for

nonperturbative benchmark

Lines from Hempel, Lattimer, G. Shen

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 35

SLIDE 47

Perturbativeness of NN potentials

0.05 0.1 0.15

n [fm-3]

5 10 15 20 25 30

E/N [MeV]

Hartree Fock 2nd order 3rd order

EGM 450/500 MeV

0.05 0.1 0.15

n [fm-3]

Hartree Fock 2nd order 3rd order

EGM 450/700 MeV

0.05 0.1 0.15

n [fm-3]

Hartree-Fock 2nd order 3rd order

EM 500 MeV

0.05 0.1 0.15

n [fm-3]

5 10 15 20 25 30 Hartree-Fock 2nd order 3rd order

POUNDerS N2LO NN

0.05 0.1 0.15

n [fm-3]

5 10 15 20 25 30

E/N [MeV]

Hartree-Fock 3rd order 2nd order

EGM 550/600 MeV

0.05 0.1 0.15

n [fm-3]

Hartree-Fock 3rd order 2nd order

EGM 600/600 MeV

0.05 0.1 0.15

n [fm-3]

Hartree-Fock 3rd order 2nd order

EGM 600/700 MeV

0.05 0.1 0.15

n [fm-3]

5 10 15 20 25 30 Hartree-Fock 3rd order 2nd order

EM 600 MeV

Krueger, IT, Hebeler, Schwenk, PRC 88 (2013)

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 36

SLIDE 48

Quantum Monte Carlo method

Solve the Schrödinger equation H | Ψ(R, τ) = − ∂

∂τ | Ψ(R, τ) , τ = i · t,

using the general solution

| Ψ(R, τ) =

• d3R′ G(R, R′, τ) | Ψ(R′, 0) .

with the propagator G(R, R′, τ)= R | e−Hτ | R′ ≈ R |

• e− V

2 ∆τe−T∆τe− V 2 ∆τN

| R′ → Analytically solvable only for local potentials: R | e− p2

i 2m ∆τ | R′ e− V(R)+V(R′) 2

∆τ

Carlson, Gandolfi, Gezerlis, PTEP (2012); Carlson, Schiavilla, RMP (1998)

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 37

SLIDE 49

Quantum Monte Carlo method

• 100
• 90
• 80
• 70
• 60
• 50
• 40
• 30
• 20

Energy (MeV)

AV18 AV18 +IL7 Expt.

0+

4He

0+ 2+

6He

1+ 3+ 2+ 1+

6Li

3/2− 1/2− 7/2− 5/2− 5/2− 7/2−

7Li

0+ 2+

8He

2+ 2+ 2+ 1+ 0+ 3+ 1+ 4+

8Li

1+ 0+ 2+ 4+ 2+ 1+ 3+ 4+ 0+

8Be

3/2− 1/2− 5/2−

9Li

3/2− 1/2+ 5/2− 1/2− 5/2+ 3/2+ 7/2− 3/2− 7/2− 5/2+ 7/2+

9Be

1+ 0+ 2+ 2+ 0+ 3,2+

10Be

3+ 1+ 2+ 4+ 1+ 3+ 2+ 3+

10B

3+ 1+ 2+ 4+ 1+ 3+ 2+ 0+ 0+

12C

Argonne v18 with Illinois-7 GFMC Calculations

24 November 2012

Carlson, Pieper, Wiringa et al. (2012)

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 38

SLIDE 50

Motivation

Chiral EFT:

◮ Systematic ◮ EFT includes nonlocal interactions

0.05 0.1 0.15 n [fm-3] 5 10 15 20 E/N [MeV]

this work LS 180 LS 220 LS 375 FSU2.1 NL3 TM1 DD2 SFHo SFHx

• 100
• 90
• 80
• 70
• 60
• 50
• 40
• 30
• 20

Energy (MeV) AV18 AV18 +IL7 Expt.

0+

4He

0+ 2+

6He

1+ 3+ 2+ 1+

6Li

3/2− 1/2− 7/2− 5/2− 5/2− 7/2−

7Li

0+ 2+

8He

2+ 2+ 2+ 1+ 0+ 3+ 1+ 4+

8Li

1+ 0+ 2+ 4+ 2+ 1+ 3+ 4+ 0+

8Be

3/2− 1/2− 5/2−

9Li

3/2− 1/2+ 5/2− 1/2− 5/2+ 3/2+ 7/2− 3/2− 7/2− 5/2+ 7/2+

9Be

1+ 0+ 2+ 2+ 0+ 3,2+

10Be

3+ 1+ 2+ 4+ 1+ 3+ 2+ 3+

10B

3+ 1+ 2+ 4+ 1+ 3+ 2+ 0+ 0+

12C

Argonne v18 with Illinois-7 GFMC Calculations

24 November 2012

Quantum Monte Carlo:

◮ Nonperturbative ◮ Need: local interactions

→ Combination of these approaches would be powerful!

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 39

SLIDE 51

Sources of nonlocality

Chiral EFT is momentum space expansion, two momenta:

• momentum transfer q = p′ − p
• momentum transfer in exchange channel k = (p′ + p)/2

Locality means:

r ′ | ˆ

V | r =

• V(r) δ(r − r ′),

if local V(r ′, r), if nonlocal After Fourier transformation, q → r but k → derivatives → nonlocal Two sources of nonlocality:

• usual regulator on relative momenta f(p) = e−(p/Λ)2n and f(p′)
• k-dependent contact interactions

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 40

SLIDE 52

Local chiral potential to N2LO

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 41

SLIDE 53

Local chiral potential to N2LO

Leading order: V (0) = V (0)

cont + VOPE

Contact potential: V (0)

cont = α1 + α2 σ1 · σ2 + α3 τ1 · τ2

+α4 σ1 · σ2 τ1 · τ2

→ only two independent (Pauli principle):

V (0)

cont = CS + CT σ1 · σ2

Regulate OPE in coordinate space: VOPE(r)

• 1 − e−(r/R0)4

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 41

SLIDE 54

Local chiral potential to N2LO

Next-to-leading order: V (2) = V (2)

cont + V (2) TPE

→ Regulate TPE in coordinate space

V (2)

cont = γ1 q2 + γ2 q2 σ1 · σ2 + γ3 q2 τ1 · τ2

+γ4 q2τ1 · τ2σ1 · σ2 +γ5 k2 + γ6 k2 σ1 · σ2 + γ7 k2 τ1 · τ2 +γ8 k2τ1 · τ2σ1 · σ2 +(σ1 + σ2)(q × k)(γ9 + γ10 τ1 · τ2) +(σ1 · q)(σ2 · q)(γ11 + γ12 τ1 · τ2) +(σ1 · k)(σ2 · k)(γ13 + γ14 τ1 · τ2)

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 42

SLIDE 55

Local chiral potential to N2LO

Next-to-leading order: V (2) = V (2)

cont + V (2) TPE

→ Regulate TPE in coordinate space

V (2)

cont = γ1 q2 + γ2 q2 σ1 · σ2 + γ3 q2 τ1 · τ2

+γ4 q2τ1 · τ2σ1 · σ2 +γ5 k2 + γ6 k2 σ1 · σ2 + γ7 k2 τ1 · τ2 +γ8 k2τ1 · τ2σ1 · σ2 +(σ1 + σ2)(q × k)(γ9 + γ10 τ1 · τ2) +(σ1 · q)(σ2 · q)(γ11 + γ12 τ1 · τ2) +(σ1 · k)(σ2 · k)(γ13 + γ14 τ1 · τ2)

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 42

SLIDE 56

Local chiral potential to N2LO

Next-to-next-to-leading order: V (3) = V (3)

TPE + V (3) IB

Regulator on contact interactions:

• dq

(2π)3 Cflocal(q2)eiq·r = C e−(r/R0)4

πΓ 3

4

• R3

Variation of cutoff R0 = 1.0 − 1.2 fm

≈ (500 − 400 MeV) ΛSFR = 1000 − 1400 MeV

Fitting of Ci to NN phase shifts

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 43

SLIDE 57

Potential in 1S0 channel

0.5 1 1.5 2 2.5

r [fm]

• 100

100 200 300 400 500

V(r) [MeV] R0 = 0.9 fm R0 = 1.0 fm R0 = 1.1 fm R0 = 1.2 fm 1S0

Note: potential is not observable! Potential in the 1S0 channel

◮ neutron-neutron system ◮ softening of the potential

when lowering the momentum space cutoff (increasing coordinate space cutoff)

Gezerlis, IT, Epelbaum, Freunek, Gandolfi, Hebeler, Nogga, Schwenk, in preparation

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 44

SLIDE 58

Phase shifts

50 100 150 200 250

• Lab. Energy [MeV]

10 20 30 40 50 60 70

Phase Shift [deg]

LO NLO N2LO

1S0

250 50 100 150 200 250

• Lab. Energy [MeV]
• 10
• 5

5 10 15 20 25 30 35 40 50 100 150 200 250

• Lab. Energy [MeV]
• 30
• 25
• 20
• 15
• 10
• 5

3P0 3P1

50 100 150 200 250

• Lab. Energy [MeV]

5 10 15 20

3P2

Comparison to EGM momentum space N2LO potentials:

Epelbaum, Glöckle, Meißner, Nucl. Phys. A (2005)

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 45

SLIDE 59

Phase shifts

50 100 150 200 250

• Lab. Energy [MeV]

10 20 30 40 50 60 70

Phase Shift [deg]

LO NLO N2LO

1S0

250 50 100 150 200 250

• Lab. Energy [MeV]
• 10
• 5

5 10 15 20 25 30 35 40 50 100 150 200 250

• Lab. Energy [MeV]
• 30
• 25
• 20
• 15
• 10
• 5

3P0 3P1

50 100 150 200 250

• Lab. Energy [MeV]

5 10 15 20

3P2

Comparison to POUNDERS N2LO potential:

Ekström et al., PRL 110 (2013)

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 46

SLIDE 60

AFDMC results for neutron matter

0.05 0.1 0.15

n [fm-3]

5 10 15

E/N [MeV]

AFDMC LO AFDMC NLO AFDMC N2LO R0=1.0 fm R0=1.2 fm

Auxiliary Field Diffusion Monte Carlo:

◮ so far only NN interaction ◮ statistical uncertainty smaller

than points

◮ order-by-order convergence up

to saturation density

◮ NLO ≈ N2LO due to large ci

Gezerlis, IT, Epelbaum, Freunek, Gandolfi, Hebeler, Nogga, Schwenk, in preparation, and PRL (2013)

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 47

SLIDE 61

AFDMC results for neutron matter

0.05 0.1 0.15 0.2

n [fm

• 3]

5 10 15

E/N [MeV]

SFR cutoff = 1000 MeV SFR cutoff = 1400 MeV

Auxiliary Field Diffusion Monte Carlo:

◮ Check influence of SRF cutoff:

Variation 1.0 − 1.4 GeV

◮ Effect less than 0.2 MeV

→ SFR cutoff has negligible effect

Gezerlis, IT, Epelbaum, Freunek, Gandolfi, Hebeler, Nogga, Schwenk, in preparation

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 48

SLIDE 62

MBPT results for neutron matter

0.05 0.1 0.15

n [fm-3]

5 10 15 20

E/N [MeV]

Hartree-Fock

N2LO R0=1.0 fm

0.05 0.1 0.15

n [fm-3]

Hartree Fock

N2LO R0=1.1 fm

0.05 0.1 0.15

n [fm-3]

5 10 15 20 Hartree Fock

N2LO R0=1.2 fm Gezerlis, IT, Epelbaum, Freunek, Gandolfi, Hebeler, Nogga, Schwenk, in preparation

Many-body perturbation theory:

◮ Hartree-Fock

u

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 49

SLIDE 63

MBPT results for neutron matter

0.05 0.1 0.15

n [fm-3]

5 10 15 20

E/N [MeV]

Hartree-Fock 2nd order

N2LO R0=1.0 fm

0.05 0.1 0.15

n [fm-3]

Hartree Fock 2nd order

N2LO R0=1.1 fm

0.05 0.1 0.15

n [fm-3]

5 10 15 20 Hartree Fock 2nd order

N2LO R0=1.2 fm Gezerlis, IT, Epelbaum, Freunek, Gandolfi, Hebeler, Nogga, Schwenk, in preparation

Many-body perturbation theory:

◮ Hartree-Fock +2nd order +3rd order (pp+hh) ◮ Bands correspond to different single-particle spectra (free, HF)

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 49

SLIDE 64

MBPT results for neutron matter

0.05 0.1 0.15

n [fm-3]

5 10 15 20

E/N [MeV]

Hartree-Fock 2nd order 3rd order

N2LO R0=1.0 fm

0.05 0.1 0.15

n [fm-3]

Hartree Fock 2nd order 3rd order

N2LO R0=1.1 fm

0.05 0.1 0.15

n [fm-3]

5 10 15 20 Hartree Fock 2nd order 3rd order

N2LO R0=1.2 fm Gezerlis, IT, Epelbaum, Freunek, Gandolfi, Hebeler, Nogga, Schwenk, in preparation

Many-body perturbation theory:

◮ Hartree-Fock +2nd order +3rd order (pp+hh) ◮ Bands correspond to different single-particle spectra (free, HF)

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 49

SLIDE 65

MBPT results for neutron matter

0.05 0.1 0.15

n [fm-3]

5 10 15 20

E/N [MeV]

AFDMC Hartree-Fock 2nd order 3rd order

N2LO R0=1.0 fm

0.05 0.1 0.15

n [fm-3]

AFDMC Hartree Fock 2nd order 3rd order

N2LO R0=1.1 fm

0.05 0.1 0.15

n [fm-3]

5 10 15 20 AFDMC Hartree Fock 2nd order 3rd order

N2LO R0=1.2 fm Gezerlis, IT, Epelbaum, Freunek, Gandolfi, Hebeler, Nogga, Schwenk, in preparation

Many-body perturbation theory:

◮ excellent agreement with AFDMC for low-cutoff potentials

(R0=1.2 fm (400 MeV))

◮ validates perturbative calculations for those interactions

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 49

SLIDE 66

MBPT results for neutron matter

0.05 0.1 0.15

n [fm-3]

5 10 15 20

E/N [MeV]

AFDMC Hartree Fock 2nd order 3rd order

NLO R0=1.0 fm

0.05 0.1 0.15

n [fm-3]

AFDMC Hartree-Fock 2nd order 3rd order

NLO R0=1.1 fm

0.05 0.1 0.15

n [fm-3]

5 10 15 20 AFDMC Hartree Fock 2nd order 3rd order

NLO R0=1.2 fm Gezerlis, IT, Epelbaum, Freunek, Gandolfi, Hebeler, Nogga, Schwenk, in preparation

Many-body perturbation theory:

◮ excellent agreement with AFDMC for low-cutoff potentials

(R0=1.2 fm (400 MeV))

◮ validates perturbative calculations for those interactions

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 50

SLIDE 67

Summary

Chiral effective field theory:

◮ Provides strong constraints for symmetry energy, neutron star EOS,

chiral condensate

◮ Inclusion of many-body forces is frontier

First QMC calculation with chiral EFT interactions

◮ Local N2LO chiral EFT potential ◮ Low-cutoff MBPT results in excellent agreement

Next (during the visit at LANL):

◮ Inclusion of leading 3N forces ◮ Use local potential in calculations of nuclei

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 51

SLIDE 68

Thanks

Thanks to my collaborators: Technische Universität Darmstadt:

• T. Krüger, K. Hebeler, B. Friman, A. Schwenk

Universität Bochum:

• E. Epelbaum

Los Alamos National Laboratory:

• S. Gandolfi

University of Guelph:

• A. Gezerlis

Forschungszentrum Jülich:

• A. Nogga

Thanks for your attention!

April 3, 2014 | Institut für Kernphysik | Theory Center | Ingo Tews | 52