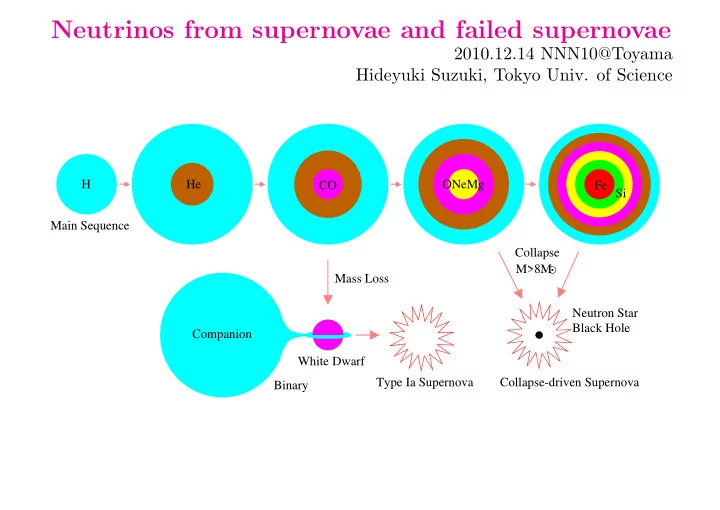
Neutrinos from supernovae and failed supernovae 2010.12.14 - PowerPoint PPT Presentation

Neutrinos from supernovae and failed supernovae 2010.12.14 NNN10@Toyama Hideyuki Suzuki, Tokyo Univ. of Science H He ONeMg CO Fe Si Main Sequence Collapse M>8M Mass Loss Neutron Star Black Hole Companion White Dwarf Type Ia Supernova Collapse-driven Supernova Binary

1 Collapse-Driven Supernova Explosion ∼ 10 14 g / cm 3 ) SN Core ( T ∼ 10MeV , ρ > • τ weak ≪ τ dyn Neutrino Trapping ⇒ Neutrinos are also in thermal equilibrium and in chemical equilibrium n ν ∼ n γ ∼ n e • mean free path length λ ν ≫ λ γ , λ e , λ N ⇒ Neutrinos carry the energy and drive the evolution of the core ⇒ SN core can be seen by neutrinos (neutrinosphere) SN as a neutrino source • source of all species ( ν e ,¯ ν e , ν µ ,¯ ν µ , ν τ ,¯ ν τ ) • T < O (100MeV) = m µ ⇒ n e − ≫ n µ , n τ : ν x ≡ ν µ , ¯ ν µ , ν τ , ¯ ν τ L ν dt ∼ O (10 53 )erg ∼ 10 4 L ν ⊙ τ ⊙ ∼ 10 2 L γ ⊙ τ ⊙ ∫ • τ ∼ O (10)sec, d > O (10 18 )cm • Spectral difference: hierarchy of average energy( O (10)MeV) σ ν e > σ ¯ ν e > σ ν x ⇒ � ω ν e � < � ω ¯ ν e � < � ω ν x � • Neutrinos pass through high density (matter and neutrinos) region( ρ = 0 ∼ 10 15 g / cm 3 ): High density MSW resonance, collective oscillation due to ν - ν interactions

H ν e He CO ONeMg Si Fe core Neutrinosphere Fe ρ >10 g/cm 11 9−10 ρ 3 c =10 g/cm 3 c ν trapping ( ρ > 10 10 − 10 12 g / cm 3 ) → ν e A ′ and e − p − ν e from e − A − → ν e n main opacity source: coherent scattering ν e A − → ν e A cross section σ ∝ A 2 ω 2 ν : λ ν A < λ ν N 10MeV ) − 1 ≫ nuclear size 1 . 2 A 1 1 ( ν wave length ¯ hc E ν 3 fm ∼ 5fm( A 3 ) E ν ∼ 20fm( 56 ) collapse σ∼ E^2 increase opaque ν trapping µ(ν) increase degenerate ν coherent nuclei survive e capture suppress scattering not so n−rich Positive feedback (Sato 1975)

ν neutronization e ν (all) burst shock stall bounce Proto Neutron 14 ρ >10 g/cm 3 c Star shock wave (collapse)~O(10−100)ms τ (neutronization burst)<O(10)ms t(stall)=O(100ms) τ Neutronization burst. Thompson et al. , ApJ 592 (2003) 434 Fig.6 (failed explosion) Shocked region e − p → n ν e A → np , σ (e − A → ν e A ′ ) < σ (e − p → ν e n)

Prompt explosion (Hillebrandt, Nomoto and Wolff 1984). M MS = 9 M ⊙ Failed Prompt explosion (Hillebrandt 1987). M MS = 20 M ⊙

Wilson’s Delayed explosion model (Colgate 1989).

shock revival ν wind PNS cooling ν heating Hot Bubble t(core exp.)=O(1)s (PNS cooling)=O(10)s τ Supernova Explosion Neutron Star Crab nebula (remnant of t(SNE)=hours−day SN1987A SN1054)

Classical Simulations Totani et al. , 1998 early phase: hierarchy of average energy late phase: n-rich matter interacts ¯ ν e and ν x almost equally. degeneracy prohibits ν e interactions, too. neutrinos from protoneutron star cooling phase (Suzuki 2002)

Energetics R Fe core − GM 2 GM 2 ( ) ∼ O (10 53 )erg • ∆ E G = core core R NS • E kin (obs . ) ∼ O (10 51 )erg , E rad (obs . ) ∼ O (10 49 )erg , E GW (sim . ) ∼ O (10 51 )erg • rest O (10 53 )erg ∼ E ν cf. E ν (SNIa) < 10 49 erg ν e ’s from neutronization of all protons 26 M Fe core � E ν e � ∼ 1 . 2 · 10 52 erg M Fe core � E ν e � 10MeV ∼ O (0 . 1) × E ν tot m Fe 1 . 4 M ⊙ = ⇒ thermal ν ≫ neutronization ν e = ⇒ ν e , ¯ ν e , ν x : roughly equipartiton

Neutrino Transfer distibution function f ν i ( t,� r, � p ν ) (7 independent variables) ( ∂f ν ) ∂f ν + d� r ∂f ν r + d� p ν ∂f ν = ∂t p dt p ∂� dt p ∂� p ν ∂t p ν int . • Spherically symmetric case: f ν i ( t, r, ω ν = p ν c, µ = cos θ ) (4 independent variables) ⇒ Fully general relativistic Boltzmann solver (Mezzacappa, Burrows, Janka, Sumiyoshi+Yamada > ∼ 2000) • Non-spherical case: 2D/3D ν transfer in progress Neutrino Interactions (minimal standard: Bruenn’85) e − p ← e + n ← e − A − → ν e A ′ e + A − ν e A ′ → ν e n → ¯ ν e p → ¯ e − e + ← → ν ¯ ν plasmon ← → ν ¯ ν NN − → NN ν ¯ ν ν e ¯ ν e ← → ν x ¯ ν x ν e ± − νν ′ − → ν e ± → νν ′ ν N − → ν N ν A − → ν A

Equation of States (EOS) for high density matter ( T � = 0 ) • Lattimer-Swesty 1991: FORTRAN code Liquid Drop model: K s = 180 , 220 , 375MeV, S v = 29 . 3MeV E/n ∼ − B + K s (1 − n/n s ) 2 / 18 + S v (1 − 2 Y e ) 2 + · · · • Shen’s EOS table (Shen et al. , 1998) RMF (n,p, σ, ρ, ω ) with TM1 parameter set( g ρ , · · · ) ⇐ Nuclear data includ- ing unstable nuclei ρ B , n B , Y e , T , F , U , P , S , A , Z , M ∗ , X n , X p , X α , X A , µ n , µ p grids: wide range T = 0 , 0 . 1 ∼ 100MeV ∆ log T = 0 . 1 Y e = 0 , 0 . 01 ∼ 0 . 56 ∆ log Y e = 0 . 025 ρ B = 10 5 . 1 ∼ 10 15 . 4 g / cm 3 ∆ log ρ B = 0 . 1 Extension with hyperons (Ishizuka, Ohnishi), quarks (Nakazato)

Modern Simulations Light ONeMg core + CO shell(1.38 M ⊙ ): weak explosion ( O (10 50 )erg) (Progenitor: Nomoto 8-10 M ⊙ ) ν -heating + nuclear reaction ⇒ weak explosion Fig. 1. Mass trajectories for the simulation with the W&H EoS as a function of post-bounce time (t pb ). Also plotted: shock position (thick solid line starting at time zero and rising to the upper right corner), gain radius (thin dashed line), and neutrinospheres ( ν e : thick solid; ¯ ν e : thick dashed; ν µ , ¯ ν µ , ν τ , ¯ ν τ : thick dash-dotted). In addition, the composition interfaces are plotted with di ff erent bold, labelled lines: the inner boundaries of the O-Ne-Mg layer at ∼ 0.77 M ⊙ , of the C-O layer at ∼ 1.26 M ⊙ , and of the He layer at 1.3769 M ⊙ . The two dot- ted lines represent the mass shells where the mass spacing between Fig. 3. Velocity profiles as functions of radius for di ff erent post - the plotted trajectories changes. An equidistant spacing of 5 × 10 − 2 M ⊙ bounce times for the simulation with the W&H EoS. The insert shows was chosen up to 1 . 3579 M ⊙ , between that value and 1 . 3765 M ⊙ it was the velocity profile vs. enclosed mass at the end of our simulation. 1 . 3 × 10 − 3 M ⊙ , and 8 × 10 − 5 M ⊙ outside. Kitaura et al. , AAp 450(2006)345 (Mezzacappa’07: 11.2 M ⊙ model explodes, too)

4 0 10 Accretion Phase Cooling Phase L/10 ν e -1 ] 3 52 erg s ν e ν µ/τ -1 2 10 L [10 1 -2 10 0 < ε > [MeV] 12 10 10 8 5 0 0.05 0.1 0.15 0.2 2 4 6 8 Time after bounce [s] Neutrino luminosities and average energies at infinity for 8.8 M ⊙ progenitor. L. H¨ udepohl et al. , PRL104 (2010) 251101

Phase transition into quark matter 53 erg/s] 53 erg/s] 1 1 Luminosity [10 Luminosity [10 0 0.255 0.26 0.265 Time after bounce [s] 0 30 rms Energy [MeV] 25 20 15 10 0 0.1 0.2 0.3 0.4 0.5 Time after bounce [s] FIG. 1: Neutrino luminosities and rms neutrino energies as functions of time after bounce, sampled at 500 km radius in the comoving frame, for a 10 M ⊙ progenitor star as modeled in [17]: ν e in solid (blue), ¯ ν e in dashed (red), and ν µ/τ in dot-dashed (green). In contrast to the deleptonization burst just after bounce ( t ∼ 5 ms) the second burst at t ∼ 257 − 261 ms is associated with the QCD phase transition. The inset shows the second burst blown up. Dasgupta et al. , PRD81 (2010) 103005 The second shock wave merges the first shock wave leading to explosion. ν e > ν e in the second burst (protonization) ¯

Modern simulations with GR 1D Boltzmann ν -transfer canonical models: no explosion Newton+O(v/c) Relativistic 3 10 Radius [km] 2 10 Fig. 1.—Trajectories of selected mass shells vs. time from the start of the simulation. The shells are equidistantly spaced in steps of 0.02 M , , and the 1 10 trajectories of the outer boundaries of the iron core (at 1.28 M , ) and of the silicon shell (at 1.77 M , ) are indicated by thick lines. The shock is formed 0 0.1 0.2 0.3 0.4 0.5 at 211 ms. Its position is also marked by a thick line. The dashed curve shows the position of the gain radius. Time After Bounce [s] WW 15 M ⊙ , M Fe = 1 . 28 M ⊙ , NR Boltzmann NH 13 M ⊙ , GR Boltzman, LS EOS+Si burning (tangent-ray method), only ν e ,¯ ν e , without Liebend¨ orfer et al. , Phys.Rev. D63 (2001) 103004 e − e + ↔ ν ¯ ν , LS EOS, Rampp et al. , ApJ 539 (astro-ph/0006418 v2) Fig.6 (2000) L33 Fig.1 10 4 10 3 radius [km] 10 2 10 1 10 0 Fig. 5. —Radial position (in km) of selected mass shells as a function of 0.0 0.2 0.4 0.6 0.8 1.0 time in our fiducial 11 M � model. NR 1D Boltzmann ν -transfer, Thompson et al. , time [sec] ApJ 592 (2003) 434 Fig.5 15 M ⊙ , Shen EOS, Sumiyoshi et al. , 2005.