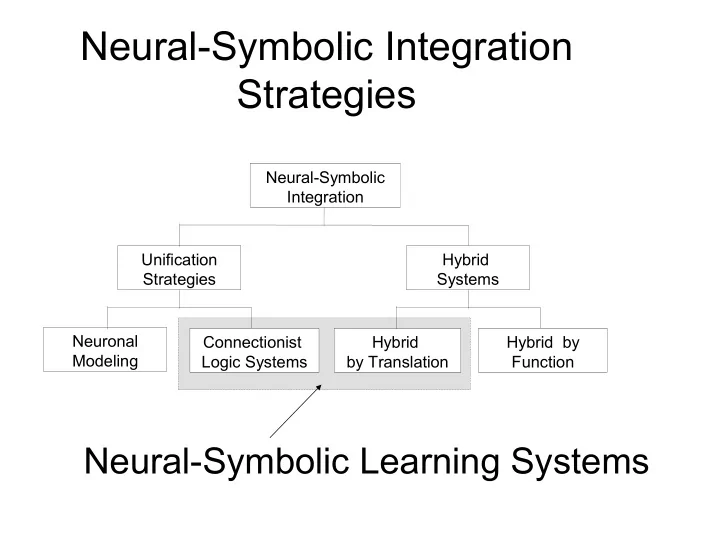
Neural-Symbolic Integration Strategies Neural-Symbolic Integration - PowerPoint PPT Presentation

Neural-Symbolic Integration Strategies Neural-Symbolic Integration Unification Hybrid Strategies Systems Neuronal Connectionist Hybrid Hybrid by Modeling Logic Systems by Translation Function Neural-Symbolic Learning Systems

CILP: Connectionist Inductive Logic Programming System Objective : To benefit from the integration of Artificial Neural Networks and Symbolic Rules. C ← F, ~G; F ← A ← B,C,~D; A ← E,F; B ← Exploiting Background Knowledge Explanation Capability Efficient Learning Massively Parallel Computation

CILP structure Connectionist System Inference Learning Machine 2 Explanation Examples 3 4 Neural Network 1 Symbolic Symbolic Knowledge Knowledge 5 1. Adding Background Knowledge (BK) 2. Computing BK in Parallel 3. Adding Training with Examples 4. Extracting Knowledge 5. Closing the Cycle

Theory Refinement Contents  Inserting Background Knowledge  Performing Inductive Learning with Examples  Adding Classical Negation  Adding Metalevel Priorities  Experimental Results

Inserting Background Knowledge A B θ A θ B Example: P = { A ← B,C,~D; W W W A ← E,F; θ 1 N 1 θ 2 N 2 θ 3 N 3 B ← } W W - W W W B C D E F Int er pr etatio ns General clause : A 0 ← A 1 …A m , ~A m+1 … ~ A n

Inserting Background Knowledge Theorem : For each general logic program P , there exists a feedforward neural network N with exactly one hidden layer and semi-linear neurons such that N computes T P . Corollary (analogous to [Holldobler and Kalinke 94]): Let P be an acceptable general program. There exists a recurrent neural network N r with semi-linear neurons such that, starting from an arbitrary initial input, N r converges to the unique stable model of P .

Computing with Background Knowledge Example: P = { A ← B,C,~D; A ← E,F; A B -(1+A min )W/2 0 B ← }. W W W Wr = 1 N1 N2 N3 Recurrently connected, N (1+A min )W (1+A min )W/2 0 converges to stable state: W W -W W W W { A = false, B = true, C = false, B C D E F T D = false, E = false, F = false } 1 Interpretations Amax Amin -1 1

CILP translation algorithm Produces neural network N given logic program P N can be trained with backpropagation subsequently Given P with clauses of the form: A if L1, ..., Lk Let p be the number of positive literals in L1, ..., Lk Let m be the number of clauses in P with A in the head Amin denotes the minimum activation for a neuron to be true Amax denotes the maximum activation for a neuron to be false Θh = (1+Amin).(k-1).W/2 (threshold of hidden neuron) ΘA = (1+Amin).(1-m).W/2 (threshold of output neuron) W > 2 (ln(1+Amin) – ln(1-Amin)) / (max(k,m).(Amin-1)+Amin+1) Amin > max(k,m)-1 / max(k,m)+1 Amax = -Amin (for simplicity)

Performing Inductive Learning with Background Knowledge • Neural Networks may be trained with examples to approximate the operator T P associated with a Logic Program P . • A differentiable activation function, e.g. the bipolar semi-linear function h(x) = (2 / (1 + e -x )) - 1, allows efficient learning with Backpropagation.

Performing Inductive Learning with Background Knowledge  We add extra input, output and hidden neurons, depending on the application  We fully-connect the network  We use Backpropagation

Adding classical negation General Program: Extended Program: Cross ← ~ Train Cross ← ¬ Train School bus crosses School bus crosses rail rail line in the absence line if there is proof of of proof of approaching no approaching train train Extended clause : L 0 ← L 1 …L m , ~L m+1 … ~ L n

The Extended CILP System A B ¬ C r 1 : A ← B, ¬C; W W W r 2 : ¬C ← B, ~ ¬E; N1 N2 N3 r 3 : B ← ~D W -W -W W W ¬ C ¬ E B D

Adding Classical Negation Theorem : For each extended logic program P , there exists a feedforward neural network N with exactly one hidden layer and semi-linear neurons such that N computes T P . Corollary : Let P be a consistent acceptable extended program. There exists a recurrent neural network N r with semi- linear neurons such that, starting from an arbitrary initial input, N r converges to the unique answer set of P .

Computing with Classical Negation Example: P = { B ← ~ C; A ¬ B B A ← B, ~ ¬ D; ¬ B ← A }. W W W N 1 N 3 N 2 Recurrently connected, N converges to stable state: -W W -W W { A = true, B = true, ¬ B = true, ¬ D A B C C = false, ¬ D = false }

Adding Metalevel Priorities ¬ x x -nW W r 1 r 2 d e b c a r1 > r2 = “ x is preferred over ¬ x ”, i.e. when r1 fires it should block the output of r2

Learning Metalevel Priorities ¬ guilty guilty P = { r 1 : guilty ← fingertips, r 2 : ¬guilty ← alibi, r 3 : guilty ← supergrass } r 1 r 2 r 3 r1 > r2 > r3 Training examples include: [(-1, 1, *), (-1, 1)] fingertips alibi super-grass [( 1, *, *), ( 1, -1)] where * means “ don’t care ”

Learning Metalevel Priorities ¬ guilty guilty W guilty, r1 = 3.97, W guilty, r2 = – 1.93, W ¬ guilty, r1 = – 1.93 r 1 r 2 r 3 W guilty, r3 = 1.94, W ¬ guilty, r2 = 1.94 W ¬ guilty, r3 = 0.00 fingertips alibi super-grass θ guilty = – 1.93, θ ¬ guilty = 1.93 r1 > r2 > r3 ?

Setting Linearly Ordered Theories W guilty,r3 = W W guilty,r2 = – W + δ ¬ guilty guilty W guilty,r1 = W guilty,r3 – W guilty,r2 + δ = 2W If W = 2, δ = 0.01: r 1 r 2 r 3 W guilty,r3 = 2 W guilty,r2 = – 1.99 W guilty,r1 = 4 fingertips alibi super-grass -3 < θ guilty < 1 r1 > r2 > r3 -1 < θ ¬ guilty < 3

Partially Ordered Theories X ¬X r2 > r1 r3 > r1 r 1 r 2 r 3 r 4 r4 > r1 Each of r 2 , r 3 and r 4 should block the conclusion of r 1

Problematic Case layEggs(platypus) monotreme(platypus) hasFur(platypus) hasBill(platypus) r1: mammal(x) ← monotreme(x) r2: mammal(x) ← hasFur(x) r1 > r3 r3: ¬ mammal(x) ← layEggs(x) r2 > r4 r4: ¬ mammal(x) ← hasBill(x) Cannot have r1 > r3, r2 > r4 without also having r1 > r4 and r2 > r3

CILP Experimental Results  Test Set Performance (how well it generalises)  Test Set Performance over small/increasing training sets (how important BK is)  Training Set Performance (how fast it trains)

CILP Experimental Results • Promoter Recognition: ♦ A short DNA sequence that preceeds the beginning of genes. Background Knowledge Promoter ← Contact, Conformation Contact ← Minus10, Minus35 ← @ -14 ‘tataat’ ← @ -13 ‘ta’, @ -10 ‘a’, @ -8 ‘t’ Minus 10 Minus 10 ← @ -13 ‘tataat’ ← @ -12 ‘ta’, @ -7 ‘t’ Minus 10 Minus 10 ← @ -37 ‘cttgac’ ← @ -36 ‘ttgac’ Minus 35 Minus 35 ← @ -36 ‘ttgaca’ ← @ -36 ‘ttg’, @ -32 ‘ca’ Minus 35 Minus 35 ← @ -45 ‘aa’, @ -41 ‘a’ Conformation Conformation ← @ -45 ‘a’, @ -41 ‘a’, @ -28 ‘tt’, @ -23 ‘t’, @ -21 ‘aa’, @ -17 ‘t’, @ -15 ‘t’, @ -4 ‘t’ Conformation ← @ -49 ‘a’, @ -44 ‘t’, @ -27 ‘t’, @ -22 ‘a’, @ -18 ‘t’, @ -16 ‘tg’, @ -1 ‘a’ Conformation ← @ -47 ‘caa’, @-43 ‘tt’, @-40 ‘ac’, @-22 ‘g’, @-18 ‘t’, @-16 ‘c’, @-8 ‘gcgcc’, @-2 ‘cc’

An Example Bioinformatics Rule Minus5 ← @-1'gc', @5't' Minus5 . . . a a g t c a g t c a g t c @-1 @1 @5

Promoter Recognition 53 examples of promoters 53 examples of non -promoters Initial Topology of the Network Minus35 Minus10 Conform. Contact Promoter -50 DNA +7 Minus35 Minus10 Conform. Contact

Test Set Performance (promoter recognition) • Comparison with systems that learn from examples only (i.e. no BK) C-IL2P 97.2 Backprop 94.3 Cobweb 94.3 P erceptron 91.5 ID3 80.2 Storm o 93.4 0 10 20 30 40 50 60 70 80 90 100 Test Set P erform ance

Test Set Performance (promoter recognition) • Comparison with systems that learn from examples and background knowledge KBCNN 98.1 C-IL2P 97.2 KBANN 92.5 Labyrinth 86.8 FOCL 85.8 E ither 79.0 0 10 20 30 40 50 60 70 80 90 100 Test Set P erformance

Test set performance on small/increasing training sets • Promoter recognition: comparison with Backprop and KBANN 0.6 0.5 0.4 B a c k p 0.3 K B A N C - I L 2 P 0.2 0.1 0 0 20 40 60 80 N u m b e r o f T r a i n i n

Training Set Performance (promoter recognition) • Comparison with Backprop and KBANN 0.6 0.5 RMS Error Rate 0.4 Backprop 0.3 KBANN C-IL2P 0.2 0.1 0 0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40 42 44 46 48 50 Training Epochs