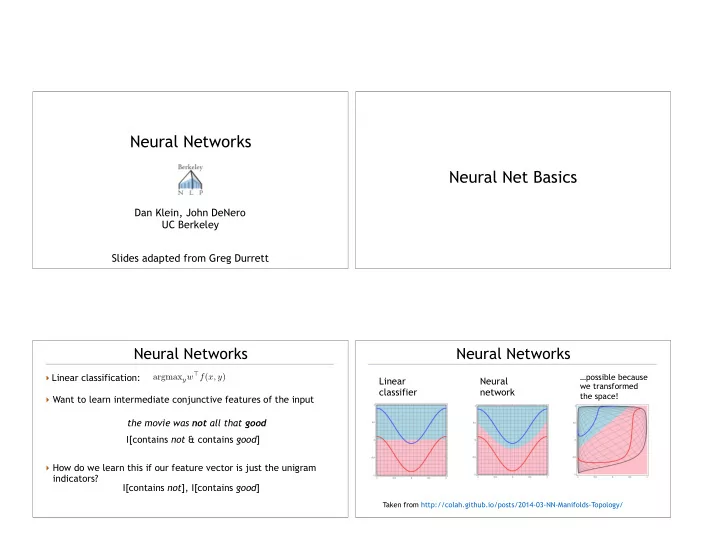
Neural Networks Neural Net Basics Dan Klein, John DeNero UC - PowerPoint PPT Presentation

Neural Networks Neural Net Basics Dan Klein, John DeNero UC Berkeley Slides adapted from Greg Durrett Neural Networks Neural Networks ‣ Linear classification: argmax y w > f ( x, y ) …possible because Linear Neural we transformed classifier network the space! ‣ Want to learn intermediate conjunctive features of the input the movie was not all that good I[contains not & contains good ] ‣ How do we learn this if our feature vector is just the unigram indicators? I[contains not ], I[contains good ] Taken from http://colah.github.io/posts/2014-03-NN-Manifolds-Topology/

Logistic Regression with NNs Neural Networks for Classification exp( w > f ( x , y )) ‣ Single scalar probability P ( y | x ) = P ( y | x ) = softmax( Wg ( V f ( x ))) y 0 exp( w > f ( x , y 0 )) P num_classes � ‣ Compute scores for all possible 
 probs d activations of "hidden" units [ w > f ( x , y )] y 2 Y labels at once (returns vector) � P ( y | x ) = softmax exp( p i ) ‣ softmax: exps and normalizes a P ( y | x ) f ( x ) softmax( p ) i = V softmax W P i 0 exp( p i 0 ) given vector z g ‣ Weight vector per class; 
 P ( y | x ) = softmax( Wf ( x )) d x n matrix num_classes x d W is [num classes x num feats] matrix nonlinearity 
 n features (tanh, relu, …) ‣ Now one hidden layer P ( y | x ) = softmax( Wg ( V f ( x ))) Objective Function Training Procedure P ( y | x ) = softmax( W z ) z = g ( V f ( x )) •Initialize parameters •For each epoch (one pass through all the training examples): ‣ Maximize log likelihood of training data observations •Shuffle the examples •Group them into mini-batches L ( x , i ∗ ) = log P ( y = i ∗ | x ) = log (softmax( W z ) · e i ∗ ) •For each mini-batch (these days often just called a "batch"): ‣ i *: index of the gold label • Compute the loss over the mini-batch ‣ e i : 1 in the i th row, zero elsewhere. This dot selects the i* th index • Compute the gradient of the loss w.r.t. the parameters • Update parameters according to a gradient-based optimizer X L ( x , i ∗ ) = W z · e i ∗ − log exp( W z ) · e j •Evaluate the current network on a held-out validation set j

Batching ‣ Batching data gives speedups due to more efficient matrix operations ‣ Need to process a batch at a time Training Tips # input is [batch_size, num_feats] 
 # gold_label is [batch_size, num_classes] def make_update(input, gold_label) ... probs = ffnn.forward(input) # [batch_size, num_classes] loss = torch.sum (torch.neg(torch.log(probs)).dot(gold_label)) ... ‣ A batch size of 32 is typical, but the best choice is 
 model & application dependent Initialization Initialization ‣ Nonlinear model…how does this affect things? 1) Can’t use zeroes for parameters to generate hidden layers: all values in that hidden layer are always 0 and have zero gradients. 2) Initialize too large and cells are saturated ‣ A common approach is random uniform/normal initialization with appropriate scale (small is typically good) " # r r ‣ Xavier Glorot (2010) 
 6 6 fan-in + fan-out , + U uniform initializer: − fan-in + fan-out ‣ If cell activations are large in absolute value, gradients are small. ‣ Want variance of inputs and gradients for each layer to be similar ‣ ReLU: Zero gradient when activation is negative.

Dropout Optimizer ‣ Probabilistically zero out some activations during training to ‣ Adam (Kingma and Ba, ICLR prevent overfitting, but use the whole network at test time 2015): very widely used. Adaptive step size + momentum ‣ Form of stochastic ‣ Wilson et al. NIPS 2017: regularization adaptive methods can ‣ Similar to benefits actually perform badly at test of ensembling: time (Adam is in pink, SGD in network needs to be black) robust to missing ‣ One more trick: gradient signals, so it has clipping (set a max value for redundancy your gradients) ‣ One line in Pytorch/Tensorflow Srivastava et al. (2014) Symbol Embeddings ‣ Words and characters are discrete symbols, 
 but input to a neural network must be real-valued ‣ Different symbols in language do have common characteristics that correlate with their distributional properties Embeddings ‣ An "embedding" for a symbol: a learned low-dimensional vector dim=128 Intuition: Low-rank approximation dim=2 to a co-occurrence matrix dim=32