n j = 0 k = 1 , 2 x x x i k k UC Irvine The above equation is - PowerPoint PPT Presentation

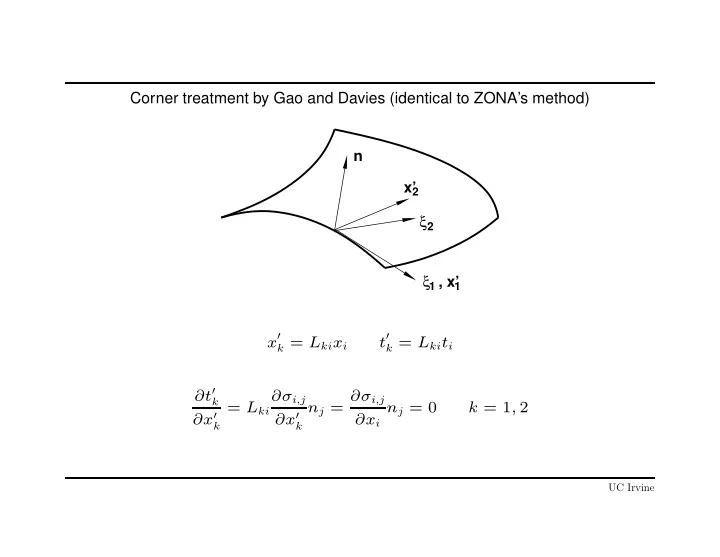
Corner treatment by Gao and Davies (identical to ZONA’s method) n x’ 2 ξ 2 1 , x’ ξ 1 x ′ t ′ k = L ki x i k = L ki t i ∂t ′ ∂σ i,j n j = ∂σ i,j k = L ki n j = 0 k = 1 , 2 ∂x ′ ∂x ′ ∂x i k k UC Irvine

The above equation is not generally valid, for several reasons: • non-zero body force ∂σ i,j = − b j � = 0 ∂x i • variation of the normal vector on a curved boundary ∂t ′ ∂ ( σ i,j n j ) ∂σ i,j k = L ki � = L ki n j ∂x ′ ∂x ′ ∂x ′ k k k • non-zero stress derivative in normal direction ∂σ i,j � = ∂σ i,j unless k = 1 , 2 , 3 L ki ∂x ′ ∂x i k UC Irvine

Generally: ∂t ′ ∂ ( σ i,j n j ) k = L ki � = 0 ∂x ′ ∂x ′ k k Problem: The stress is not given and cannot be expressed in terms of displacements, because it would involve displacement derivatives in normal direction which are not known. Is it possible to formulate an accurate/exact equation that involves only variations on the boundary? UC Irvine