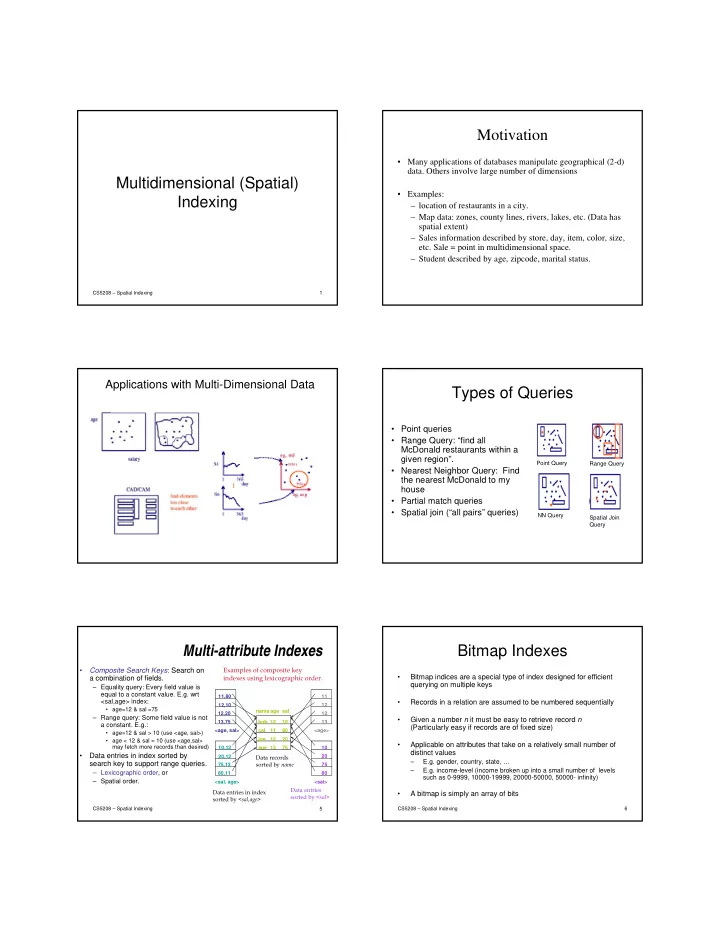
Motivation Many applications of databases manipulate geographical - PDF document

Motivation • Many applications of databases manipulate geographical (2-d) data. Others involve large number of dimensions Multidimensional (Spatial) • Examples: Indexing – location of restaurants in a city. – Map data: zones, county lines, rivers, lakes, etc. (Data has spatial extent) – Sales information described by store, day, item, color, size, etc. Sale = point in multidimensional space. – Student described by age, zipcode, marital status. CS5208 – Spatial Indexing 1 Applications with Multi-Dimensional Data Types of Queries • Point queries • Range Query: “find all McDonald restaurants within a given region”. Point Query Range Query • Nearest Neighbor Query: Find the nearest McDonald to my house • Partial match queries • Spatial join (“all pairs” queries) NN Query Spatial Join Query Multi-attribute Indexes Bitmap Indexes Examples of composite key • Composite Search Keys : Search on • Bitmap indices are a special type of index designed for efficient a combination of fields. indexes using lexicographic order. querying on multiple keys – Equality query: Every field value is equal to a constant value. E.g. wrt 11,80 11 <sal,age> index: • Records in a relation are assumed to be numbered sequentially 12,10 12 • age=12 & sal =75 name age sal 12,20 12 – Range query: Some field value is not • Given a number n it must be easy to retrieve record n 13,75 bob 12 10 13 a constant. E.g.: (Particularly easy if records are of fixed size) <age, sal> cal 11 80 <age> • age=12 & sal > 10 (use <age, sal>) joe 12 20 • age < 12 & sal = 10 (use <age,sal> • Applicable on attributes that take on a relatively small number of may fetch more records than desired) 10,12 sue 13 75 10 distinct values • Data entries in index sorted by Data records 20 20,12 – E.g. gender, country, state, … search key to support range queries. sorted by name 75,13 75 – E.g. income-level (income broken up into a small number of levels – Lexicographic order, or 80,11 80 such as 0-9999, 10000-19999, 20000-50000, 50000- infinity) – Spatial order. <sal, age> <sal> Data entries Data entries in index • A bitmap is simply an array of bits sorted by <sal> sorted by <sal,age> CS5208 – Spatial Indexing 5 CS5208 – Spatial Indexing 6

Use of Bitmap Indexes: Example Bitmap Indexes (Cont.) • In its simplest form, a bitmap index on an attribute has a bitmap for each value of the attribute • Queries are answered using logical (bitwise) operations – Bitmap has as many bits as records – Intersection (and) – In a bitmap for value v, the bit for a record is 1 if the record has the – Union (or) value v for the attribute, and is 0 otherwise – Complementation (not) – Size = nm bits where n is the #records, m is the #distinct values • Each operation takes two bitmaps of the same size and applies the operation on corresponding bits to get the result bitmap – Males with income level L1 • 10010 AND 10100 = 10000 • Can then retrieve required tuples • Counting number of matching tuples is even faster • Range queries? – Age IN [30,40] AND Salary IN [10k,20k] 7 CS5208 – Spatial Indexing 8 CS5208 – Spatial Indexing Compressed Bitmaps Compressed Bitmap (Cont.) • If n and m are large, then nm bits may incur high I/O • Consider 0000000000000110001 • Compress the bitmap – run-length encoding – The encoded sequence is … – A sequence of i 0’s followed by a 1 (run) is represented by some binary encoding of the integer i • Now consider 000000010000 (i.e., n = 12) – A number i is represented by (log 2 i -1) 1-bit (indicates • What is the compressed bitmap? the number of bits required to represent i ) and a single 0, followed by its binary value • E.g., 13 = 1101 (binary) is represented as 111 0 1101 • Decode 110111 13 log13-1 • Exceptions: i = 0 is 00; i = 1 is 01 – What about the (missing) 0’s? – Every run incurs 2 log 2 i bits CS5208 – Spatial Indexing 9 CS5208 – Spatial Indexing 10 Operating on Compressed Bitmap Operating on Compressed Bitmap • Need to decode first, then perform the • Need to decode first, then perform the bitwise operations bitwise operations • But can be done incrementally • But can be done incrementally • Suppose we ORed encodings: • Suppose we ORed encodings: 0 0 1 1 0 1 1 1 1 1 0 1 1 1 0 0 1 1 0 1 1 1 1 1 0 1 1 1 7 7 7 0 0 00000001 00000001 0 0 00000001 OUTPUT: 0 OUTPUT: 0 0 0 0 0 0 0 1 CS5208 – Spatial Indexing 11 CS5208 – Spatial Indexing 12

Why spatial index methods (SAMs)? Operating on Compressed Bitmap • B-tree & hash tables – Guarantee the number of I/O operations is • Need to decode first, then perform the respectively logarithmic and constant with respect bitwise operations to the collection’s size – Index a collection on a key • But can be done incrementally – Rely on a total order on the key domain, the order • Suppose we ORed encodings: of natural numbers, or the lexicographic order on strings 0 0 1 1 0 1 1 1 1 1 0 1 1 1 • There is no such total order for multidimensional objects and geometric 7 7 0 objects with spatial extent 00000001 0 00000001 • SAMs were designed to try as much as OUTPUT: 0 0 0 0 0 0 0 1 1 possible to preserve spatial object proximity CS5208 – Spatial Indexing 13 CS5208 – Spatial Indexing 14 Multidimensional Indexing Structures Grid File: A Space-based Approach • Space-Based structures: – Partition the embedding Space into rectangular cells – Independent from the distribution of the objects • Start with one bucket – Objects are mapped to the cells based on some geometric criterion for the whole space. – Eg: Grid file, Buddy-tree, KDB-tree • Data-Based structures: • Select dividers along – Organize by partitioning the set of objects based on spatial proximity such that each group can fit into a page each dimension. – Adapt to the objects’ distribution Partition space into – Eg. R-tree, R* tree, R+ tree • Mapping cells – Transform the data into lower dimensional space • Dividers cut all the – E.g., space filling curve way CS5208 – Spatial Indexing 15 CS5208 – Spatial Indexing 16 Grid File Implementation Grid File • Dynamic structure using a grid directory • Each cell corresponds to 1 disk page. – Grid array: a 2 dimensional array with • Many cells can point pointers to buckets (this array can be large, to the same page. disk resident) G(0,…, nx-1, 0, …, ny-1) • Cell directory – Linear scales: Two 1 dimensional arrays that potentially exponential in the number of used to access the grid array (main memory) dimensions X(0, …, nx-1), Y(0, …, ny-1) CS5208 – Spatial Indexing 17 CS5208 – Spatial Indexing 18