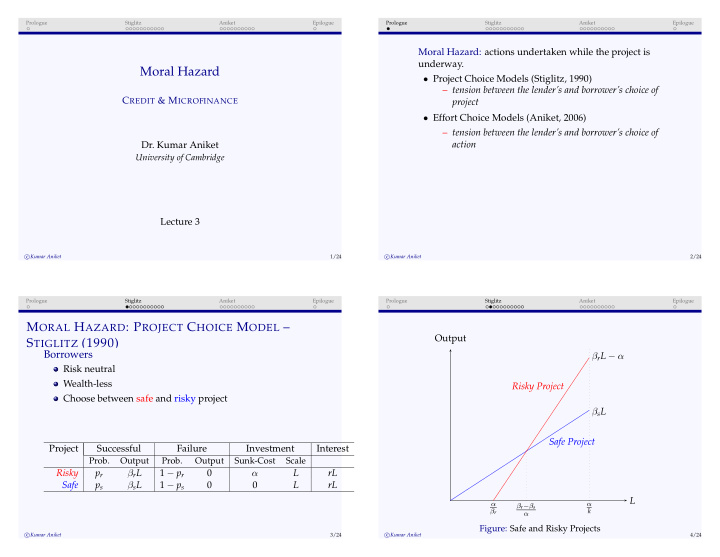



Prologue Stiglitz Aniket Epilogue Prologue Stiglitz Aniket Epilogue Moral Hazard: actions undertaken while the project is underway. Moral Hazard • Project Choice Models (Stiglitz, 1990) – tension between the lender’s and borrower’s choice of C REDIT & M ICROFINANCE project • Effort Choice Models (Aniket, 2006) – tension between the lender’s and borrower’s choice of action Dr. Kumar Aniket University of Cambridge Lecture 3 � Kumar Aniket c 1/24 � Kumar Aniket c 2/24 Prologue Stiglitz Aniket Epilogue Prologue Stiglitz Aniket Epilogue M ORAL H AZARD : P ROJECT C HOICE M ODEL – Output S TIGLITZ (1990) Borrowers β r L − α Risk neutral Wealth-less Risky Project Choose between safe and risky project β s L Safe Project Project Successful Failure Investment Interest Prob. Output Prob. Output Sunk-Cost Scale Risky p r β r L 1 − p r 0 α L rL Safe p s β s L 1 − p s 0 0 L rL L α α β r − β s k β r α Figure: Safe and Risky Projects � Kumar Aniket c 3/24 � Kumar Aniket c 4/24
Prologue Stiglitz Aniket Epilogue Prologue Stiglitz Aniket Epilogue B ORROWER ’ S P AYOFF FROM THE TWO PROJECTS I NDIVIDUAL L ENDING S WITCH L INE Switch Line: Locus of contracts ( r , L ) along which the Safe Project: Lower expected marginal return & 0 sunk borrower is indifferent between risky and safe project cost V s = p s ( β s L − rL ) V r > V s Risky Project: Higher expected marginal return & α sunk cost p r ( β r L − rL ) − α > p s ( β s L − rL ) V r = p r ( β r L − rL ) − α α L > (Output threshold) ∆ pr + k Assumption p r β r − p s β s = k Northeast of the switch line: Sunk cost investment α is overwhelmed by increased expected marginal productivity of . . . difference in expected marginal return constant risky project k and saving on the expected interest rate payment ∆ pr . � Kumar Aniket c 5/24 � Kumar Aniket c 6/24 Prologue Stiglitz Aniket Epilogue Prologue Stiglitz Aniket Epilogue L ENDER ’ S Z ERO P ROFIT C ONDITION r Risk adjusted interest rate r = ρ i = s , f (L-ZPC) p i Optimal Contract ( r ∗ , L ∗ ) : Switch line & (L-ZPC) Maximum loan size & Interest Rate α L ∗ = � � ρ ∆ p + k p s r ∗ = ρ L p s Figure: Switch Line � Kumar Aniket c 7/24 � Kumar Aniket c 8/24
b b b Prologue Stiglitz Aniket Epilogue Prologue Stiglitz Aniket Epilogue G ROUP L ENDING r Borrower’s payoffs V ss = p s ( β s L − rL ) − p s ( 1 − p s ) cL V rr = p r ( β r L − rL ) − α − p r ( 1 − p r ) cL ρ p r Joint liability payment c incurred with probability p i ( 1 − p i ) ρ Optimal Contract p s Payoffs ↓ due to the joint liability payment c Payoffs ↑ due to larger loans L α ∆ p ρ ps + k Figure: Switch Line and Optimal Contract under Individual Lending � Kumar Aniket c 9/24 � Kumar Aniket c 10/24 Prologue Stiglitz Aniket Epilogue Prologue Stiglitz Aniket Epilogue G ROUP L ENDING S WITCH L INE r Group Lending Switch Line: Lender’s Zero Profit Condition: α L = � ρ ∆ pr + k − ∆ p ( p s + p r − 1 ) c � � 1 − p s � r = − c p s p s Maximum Loan Size in Group Lending: ρ α p s where ϕ = L ∗ = “ 1 − p s Group Contract ” � � p s − ( 1 − p s ) c ∆ p + ( p s + p r − 1 ) ρ � � ρ p s ∆ p + k − ϕ c p s p s L Joint liability payment lets borrowers get larger loans α ∆ p ρ ps + k − ϕ c . . . L ∗ is increasing in c Figure: Switch Line and Optimal Contract under Group Lending � Kumar Aniket c 11/24 � Kumar Aniket c 12/24
Prologue Stiglitz Aniket Epilogue Prologue Stiglitz Aniket Epilogue P ROJECT C HOICE S UMMARY F IRST B EST Lender curtails loan size to prevent borrowers undertaking Borrower chooses π i � . . . π i where π h > π l x Project: risky loans with significantly high sunk cost − 1 → . . . 1 − π i Private Benfits B with π l 0 Individual liability loans Joint liability group loans Borrower’s Participation Constraint Borrower pay ρ Borrower pay ρ 1 1 π h ( x − r ) � 0 Lower risk exposure Higher risk exposure 2 2 Lender’s Zero Profit Constraint Small Loans Larger Loans 3 3 r � ρ May explain why we find the poorer section of our society are π h not able to undertake profitable investment Contract Space r Borrowers interact Can lender do better by ρ Socially Viable Projects x 0 π h cooperatively and not making the borrowers strategically amongst interact strategically Figure: First Best � Kumar Aniket c 13/24 � Kumar Aniket c 14/24 themselves amongst themselves Prologue Stiglitz Aniket Epilogue Prologue Stiglitz Aniket Epilogue S ECOND B EST Borrower’s Participation Lender’s Zero Profit Constraint m B Constraint r � ρ π h B(0) m π h ( x − r ) � 0 Borrower’s Incentive Compatibility Constraint π h ( x − r ) � π l ( x − r ) + B borrower’s monitor’s private benefits monitoring costs B x − r � ∆ π B(m) 45º m m B Contract Space ∆ π r Figure: Monitoring Function ρ B x − x 0 π h ∆ π Figure: Second Best � Kumar Aniket c 15/24 � Kumar Aniket c 16/24
Prologue Stiglitz Aniket Epilogue Prologue Stiglitz Aniket Epilogue D ELEGATED M ONITORING Borrower’s Participation Lender’s Zero Profit Constraint m Constraint r � ρ B(m)+m B(0) π h m π h ( x − r ) � 0 Borrower’s Incentive Monitor’s Incentive Compatibility Compatibility Constraint Constraint B(m * ) borrower’s monitor’s π h w − m � π l w π h ( x − r ) � π l ( x − r ) + B m * private benefits monitoring costs w � m B x − r � ∆ π B(m) ∆ π 45º 45º m m * m * m B ( m ) m Contract Space Figure: Optimal Monitoring Level ∆ π ∆ π r ρ x − B ( m ) − m x 0 π h ∆ π Figure: Delegated Monitoring � Kumar Aniket c 17/24 � Kumar Aniket c 18/24 Prologue Stiglitz Aniket Epilogue Prologue Stiglitz Aniket Epilogue S IMULTANEOUS G ROUP L ENDING x-r Multi-task environment: Borrower’s payoff + when α( B (0)+ m ) ) B E both projects succeed. Monitoring and exerting effort C Otherwise 0. B (0) The contract space is determined by the following two H m constraints. A α B (0) The individual borrower’s ICC for high effort when her peer G 1 exerts high effort and both choose m . B ( m ) π h π h ( x − r ) − m � π l π h ( x − r ) + B ( m ) − m The group’s collective compatibility condition such that D 2 m the group has the incentive to undertake both tasks m sim m seq O collectively. Figure: Monitoring Intensities in Group Lending ( π h ) 2 ( x − r ) − m � ( π l ) 2 ( x − r ) + B ( 0 ) � Kumar Aniket c 19/24 � Kumar Aniket c 20/24 1 π h r � x − π h ∆ π max [ B ( m ) , α ( B ( 0 ) + m )] where α = ։ π h + π l
Prologue Stiglitz Aniket Epilogue Prologue Stiglitz Aniket Epilogue S EQUENTIAL G ROUP L ENDING : A NIKET (2006) S EQUENTIAL G ROUP L ENDING WITH ALMOST P ERFECT I NFORMATION Borrower 1 gets the loan while Borrower 2 is waiting for loan As monitoring becomes more efficient, we get closer to the � Borrower 2 only gets loan if the Borrower 1 succeeds first best world or to almost perfect information. � Contract space determined by following constraints: 1 � � r � x − π h ∆ π max B ( m ) , m Simultaneous Lending Sequential Lending Payoff driven down to Payoffs driven down to 0. α B ( 0 ) First Best Only the more expensive individual task has to be Far from First Best incentivised Group’s collective incentive constraint does not have to Lender is able to reduce rent by lending sequentially satisfied. A greater range of project would be financed under Borrowers are interacting strategically and not co-operatively sequential lending Borrower’s obtain lower rents and a larger surplus is created � Kumar Aniket c 21/24 � Kumar Aniket c 22/24 Prologue Stiglitz Aniket Epilogue Prologue Stiglitz Aniket Epilogue C ONCLUSIONS x-r Stiglitz (1990) α( B (0 , )+ m ) β Shows that cooperative group lending increases loan size B (0 , β ) Aniket (2006) With almost perfect information, cooperative group lending relatively inefficient c shows sequential lending lower the productivity threshold B ( m, ) β to finance the projects α B (0 , ) β Especially useful if poorest have extremely low productivity project β m m sim m seq O Figure: Monitoring Intensities as Monitoring Efficiency Increases � Kumar Aniket c 23/24 � Kumar Aniket c 24/24
Recommend
More recommend