Medium-Mass Nuclei from First Principles Jason D son D. H . Holt - PowerPoint PPT Presentation

Medium-Mass Nuclei from First Principles Jason D son D. H . Holt olt 2v 1q1v 2q 3p1h 4p2h 2v 1q1v 2q 3p1h 4p2h

Drip Lines and Magic Numbers: The Evolving Nuclear Landscape Physics of exotic nuclei – era of coming decades What are the limits of nuclear existence? How do magic numbers form and evolve? 82 ! 126 ! Undiscovered 50 ! stable nuclei protons 82 ! known nuclei 28 ! 20 ! 50 ! 8 ! 28 ! 2 ! 20 ! 8 ! 2 ! neutrons

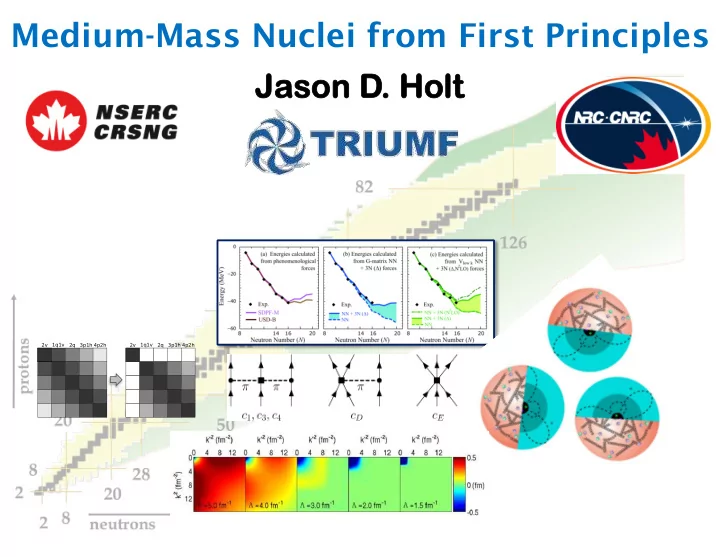
Drip Lines and Magic Numbers: 3N Forces in Medium-Mass Nuclei Exploring the frontiers of nuclear science: Worldwide joint experimental/theoretical effort What are the properties of proton/neutron-rich matter? What are the limits of nuclear existence? 82 ! Heavie viest o st oxy xygen isotope n isotope How do magic numbers form and evolve? 126 ! 0 (a) Energies calculated (b) Energies calculated (c) Energies calculated from phenomenological from G-matrix NN from V NN low k 2 forces + 3N ( ∆ ) forces + 3N ( ∆ ,N LO ) forces Energy (MeV) − 20 50 ! protons − 40 Exp. Exp. Exp. 2 SDPF-M 82 ! NN + 3N (N LO) NN + 3N ( ∆ ) NN + 3N ( ∆ ) USD-B NN NN − 60 8 14 16 20 8 14 16 20 8 14 16 20 28 ! Neutron Number ( N ) Neutron Number ( N ) Neutron Number ( N ) 20 ! 50 ! Otsuka, Suzuki, JDH, Schwenk, Akaishi, PRL (2010) 8 ! 28 ! π π π 2 ! 20 ! 8 ! 2 ! neutrons

Limits of Empirical Approach What are the properties of proton/neutron-rich matter? What are the limits of existence of matter? How do magic numbers form and evolve? Worldwide joint experimental/theoretical effort! 82 ! N=3 =34 m magic gic n num umbe ber in c r in calc lcium ium? 6 (a) Phenomenological Forces 5 + Energy (MeV) 126 ! 4 3 2 50 ! protons 1 1 2 0 82 ! Experiment GXPF1 KB3G 28 ! 20 ! 50 ! 42 44 46 48 50 52 54 56 58 Mode Model de l depe pende ndent e nt extr xtrapola polations tions 8 ! 28 ! Dif iffic icult to e ult to extr xtract phy t physic sics: c s: contin ontinuum uum, de , deform ormation tion 2 ! 20 ! Aim im: pr : predic dictiv tive ab ab initio the initio theory f ory far fr r from om sta stability bility 8 ! 2 ! neutrons

Drip Lines and Magic Numbers: 3N Forces in Medium-Mass Nuclei Exploring the frontiers of nuclear science: Worldwide joint experimental/theoretical effort What are the properties of proton/neutron-rich matter? What are the limits of nuclear existence? 82 ! New m w magic gic n num umbe bers in c s in calc lcium ium How do magic numbers form and evolve? 6 + Energy (MeV) 5 126 ! 4 3 2 50 ! 1 1 protons 2 0 NN NN+3N 82 ! NN+3N (MBPT) 44 48 52 56 60 64 68 28 ! Mass Number A 20 ! JDH, Otsuka, Schwenk, Suzuki, JPG (2012) 50 ! JDH, Menendez, Schwenk, JPG (2013) 8 ! 28 ! π π π 2 ! 20 ! 8 ! 2 ! neutrons

Drip Lines and Magic Numbers: 3N Forces in Medium-Mass Nuclei Exploring the frontiers of nuclear science: Worldwide joint experimental/theoretical effort What are the properties of proton/neutron-rich matter? What are the limits of nuclear existence? 82 ! New m w magic gic n num umbe bers in c s in calc lcium ium How do magic numbers form and evolve? 6 + Energy (MeV) 5 126 ! 4 3 2 50 ! 1 1 protons 2 0 NN NN+3N 82 ! NN+3N (MBPT) 44 48 52 56 60 64 68 28 ! Mass Number A 20 ! JDH, Otsuka, Schwenk, Suzuki, JPG (2012) 50 ! JDH, Menendez, Schwenk, JPG (2013) 8 ! 28 ! π π π 2 ! 20 ! 8 ! 2 ! neutrons

Drip Lines and Magic Numbers: 3N Forces in Medium-Mass Nuclei LETTER Exploring the frontiers of nuclear science: doi:10.1038/nature12522 Worldwide joint experimental/theoretical effort Evidence for a new nuclear ‘magic number’ from the What are the properties of proton/neutron-rich matter? level structure of 54 Ca What are the limits of nuclear existence? 82 ! New m w magic gic n num umbe bers in c s in calc lcium ium D. Steppenbeck 1 , S. Takeuchi 2 , N. Aoi 3 , P. Doornenbal 2 , M. Matsushita 1 , H. Wang 2 , H. Baba 2 , N. Fukuda 2 , S. Go 1 , M. Honma 4 , J. Lee 2 , K. Matsui 5 , S. Michimasa 1 , T. Motobayashi 2 , D. Nishimura 6 , T. Otsuka 1,5 , H. Sakurai 2,5 , Y. Shiga 7 , P.-A. So ¨m 2 , ¨derstro How do magic numbers form and evolve? ´n 10 & K. Yoneda 2 T. Sumikama 8 , H. Suzuki 2 , R. Taniuchi 5 , Y. Utsuno 9 , J. J. Valiente-Dobo 6 LETTER + Energy (MeV) 5 126 ! doi:10.1038/nature12226 4 3 Masses of exotic calcium isotopes pin down 2 nuclear forces 50 ! 1 1 protons 2 F. Wienholtz 1 , D. Beck 2 , K. Blaum 3 , Ch. Borgmann 3 , M. Breitenfeldt 4 , R. B. Cakirli 3,5 , S. George 1 , F. Herfurth 2 , J. D. Holt 6,7 , 0 NN M. Kowalska 8 , S. Kreim 3,8 , D. Lunney 9 , V. Manea 9 , J. Mene ´ndez 6,7 , D. Neidherr 2 , M. Rosenbusch 1 , L. Schweikhard 1 , A. Schwenk 7,6 , J. Simonis 6,7 , J. Stanja 10 , R. N. Wolf 1 & K. Zuber 10 NN+3N 82 ! NN+3N (MBPT) 44 48 52 56 60 64 68 28 ! Mass Number A 20 ! JDH, Otsuka, Schwenk, Suzuki, JPG (2012) 50 ! JDH, Menendez, Schwenk, JPG (2013) 8 ! 28 ! π π π 2 ! 20 ! 8 ! 2 ! neutrons

Approaches to Nuclear Structure “The first, the basic approach, is to study the elementary particles, their properties and mutual interaction. Thus one hopes to obtain knowledge of the nuclear forces. If the forces are known, one should, in principle, be able to calculate deductively the properties of individual nuclei. Only after this has been accomplished can one say that one completely understands nuclear structure… The other approach is that of the experimentalist and consists in obtaining by direct experimentation as many data as possible for individual nuclei. One hopes in this way to find regularities and correlations which give a clue to the structure of the nucleus... The shell model, although proposed by theoreticians, really corresponds to the experimentalist’s approach.” – M. Goeppert-Mayer, Nobel Lecture Ab initio approach vs. phenomenological Theories of medium-mass nuclei largely empirical Purpose of lectures is to show how shell model can be based on the first approach!

The Challenge of Ab Initio Nuclear Theory To understand the properties of complex nuclei from first principles Two significant issues: Interaction Not well understood Not obtainable from QCD Too “hard” to be useful Multiple energy scales Many-body Problem Not ‘exactly’ solvable above A ∼ 20 Here we focus on shell model

The Challenge of Ab Initio Nuclear Theory To understand the properties of complex nuclei from first principles Two significant issues: Interaction Not well understood Not obtainable from QCD Too “hard” to be useful Multiple energy scales Many-body Problem Not ‘exactly’ solvable above A ∼ 20 Here we focus on shell model

The Challenge of Ab Initio Nuclear Theory To understand the properties of complex nuclei from first principles Two significant issues: Interaction Not well understood Not obtainable from QCD Too “hard” to be useful Multiple energy scales Many-body Problem Not ‘exactly’ solvable above A ∼ 20 Here we focus on shell model How will we approach this problem: QCD ! NN (3N) forces ! Renormalize ! “Solve” many-body problem ! Predictions

The Challenge of Ab Initio Nuclear Theory To understand the properties of complex nuclei from first principles Nucleon-nucleon interaction Some history Anatomy of an NN interaction Construction from QCD? Ideas of Effective Field Theory Chiral EFT for nuclear forces Constraint by data How will we approach this problem: QCD ! NN (3N) forces ! Renormalize ! “Solve” many-body problem ! Predictions

The Challenge of Ab Initio Nuclear Theory To understand the properties of complex nuclei from first principles Renormalizing NN Interactions Basic ideas of RG Low-momentum interactions Similarity RG interactions Benefits of low cutoffs G-matrix renormalization How will we approach this problem: QCD ! NN (3N) forces ! Renormalize ! “Solve” many-body problem ! Predictions

The Challenge of Ab Initio Nuclear Theory To understand the properties of complex nuclei from first principles Microscopic Valence- Space Interactions Model spaces Many-body perturbation theory (MBPT) Calculating effective interaction In-medium Similarity RG Monopole part of interaction Deficiencies of this approach How will we approach this problem: QCD ! NN (3N) forces ! Renormalize ! “Solve” many-body problem ! Predictions

The Challenge of Ab Initio Nuclear Theory To understand the properties of complex nuclei from first principles Three-Nucleon Forces a b c Basic ideas – why needed? 3N from chiral EFT Implementing in shell model Relation to monopoles Predictions/new discoveries Connections beyond structure How will we approach this problem: QCD ! NN (3N) forces ! Renormalize ! “Solve” many-body problem ! Predictions

Part I: The Nucleon-Nucleon Interaction To understand the properties of complex nuclei from first principles Nucleon-nucleon interaction Some history Anatomy of an NN interaction Construction from QCD? Ideas of Effective Field Theory Chiral EFT for nuclear forces Constraint by data How will we approach this problem: QCD ! NN (3N) forces ! Renormalize ! Solve many-body problem ! Predictions