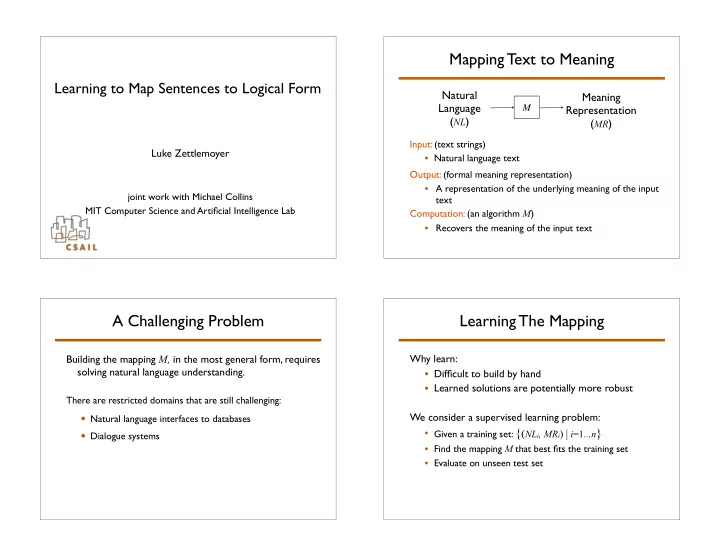
Mapping Text to Meaning Learning to Map Sentences to Logical Form - PowerPoint PPT Presentation

Mapping Text to Meaning Learning to Map Sentences to Logical Form Natural Meaning Language M Representation ( NL ) ( MR ) Input: (text strings) Luke Zettlemoyer • Natural language text Output: (formal meaning representation) • A representation of the underlying meaning of the input joint work with Michael Collins text MIT Computer Science and Artificial Intelligence Lab Computation: (an algorithm M ) • Recovers the meaning of the input text A Challenging Problem Learning The Mapping Why learn: Building the mapping M, in the most general form, requires solving natural language understanding. • Difficult to build by hand • Learned solutions are potentially more robust There are restricted domains that are still challenging: We consider a supervised learning problem: • Natural language interfaces to databases • Given a training set: { ( NL i , MR i ) | i =1 ...n } • Dialogue systems • Find the mapping M that best fits the training set • Evaluate on unseen test set

The Setup for This Talk A Simple Training Example NL : A single sentence Given training examples like: • usually a question Input: What states border Texas? MR : A lambda-calculus expression Output: � x.state ( x ) � borders ( x,texas ) • similar to meaning representations used in formal semantics classes in linguistics MR : Lambda calculus M : Weighted combinatory categorical grammar (CCG) • Can think of as first-order logic with functions • mildly context-sensitive formalism • Useful for defining the semantics of questions • explains a wide range of linguistic phenomena: Challenge for learning: coordination, long distance dependencies, etc. • Derivations (parses) are not in training set • models syntax and semantics • statistical parsing algorithms exist • We need to recover this missing information More Training Examples Outline • Combinatory Categorial Grammars (CCG) Input: What is the largest state? Output: argmax ( � x.state ( x ) , � x.size ( x )) • A learning algorithm: structure and parameters Input: What states border the largest state? Output: � x.state ( x ) � borders ( x, • Extensions for spontaneous, unedited text argmax ( � y.state ( y ) , � y.size ( y ))) Input: What states border states that border • Future Work: Context-dependent sentences states ... that border Texas? Output: � x.state ( x ) � ∃ y.state ( y ) � ∃ z.state ( z ) � ... � borders ( x,y) � borders ( y,z) � borders ( z,texas)

CCG CCG Lexicon [Steedman 96,00] Category Lexicon Words • Pairs natural language phrases with syntactic and Syntax : Semantics semantic information Texas NP : texas • Relatively complex: contains almost all information used during parsing Kansas NP : kansas borders (S\NP)/NP : � x. � y.borders ( y,x ) Parsing Rules (Combinators) • Small set of relatively simple rules state N : � x.state ( x ) • Build parse trees bottom-up Kansas City NP : kansas_city_MO • Construct syntax and semantics in parallel ... ... Parsing: Lexical Lookup Parsing Rules (Combinators) Application • X/Y : f Y : a => X : f(a) What states border Texas (S\NP)/NP S\NP NP NP S/(S\NP)/N N (S\NP)/NP � x. � y.borders ( y,x ) � y.borders ( y,texas ) texas � f. � g. � x.f(x) � g(x) � x.state(x) � x. � y.borders ( y,x ) texas • Y : a X\Y : f => X : f(a) NP S\NP S � y.borders ( y,texas ) kansas borders ( kansas,texas )

Parsing a Question Parsing Rules (Combinators) Application • X/Y : f Y : a => X : f(a) What states border Texas • Y : a X\Y : f => X : f(a) NP S/(S\NP)/N N (S\NP)/NP � f. � g. � x.f(x) � g(x) � x.state(x) � x. � y.borders ( y,x ) texas Composition S/(S\NP) S\NP • X/Y : f Y/Z : g => X/Z : � x.f(g(x)) � g. � x.state(x) � g(x) � y.borders ( y,texas ) • Y\Z : g X\Y : f => X\Z : � x.f(g(x)) S � x.state(x) � borders(x,texas) Other Combinators • Type Raising • Crossed Composition Features, Weights and Scores Weighted CCG x= border Texas What states Weighted linear model ( � , f , w ) : (S\NP)/NP S/(S\NP)/N N NP � x.state(x) � x. � y.borders ( y,x ) texas � f. � g. � x.f(x) � g(x) • CCG lexicon: � y= S/(S\NP) S\NP � g. � x.state(x) � g(x) � y.borders ( y,texas ) • Feature function: f ( x,y ) ∈ R m S � x.state(x) � borders(x,texas) • Weights: w ∈ R m Lexical count features: Quality of a parse y for sentence x f ( x,y ) = [ 0, 1, 0, 1, 1, 0, 0, 1, ... , 0] • Score: w · f ( x,y ) w = [-2, 0.1, 0, 2, 1, -3, 0, 0.3, ..., 0] w · f ( x,y ) = 3.4

Weighted CCG Parsing Outline Two computations: sentence x , parses y, LF z • Combinatory Categorial Grammars (CCG) • Best parse • A learning algorithm: structure and y * = argmax w � f ( x , y ) parameters y • Best parse with logical form z • Extensions for spontaneous, unedited text y = arg y s . t . L ( y )= z w · f ( x , y ) ˆ max • Future Work: Context-dependent sentences We use a CKY -style dynamic-programming algorithm with pruning A Supervised Learning Approach Learning: Two Parts Given a training set: {( x i , z i ) | i =1 ...n } • GENLEX subprocedure • x i : a natural language sentence • Create an overly general lexicon • z i : a lambda-calculus expression • A full learning algorithm Find a weighted CCG that minimizes error • Prunes the lexicon and estimates • induce a lexicon � parameters w • estimate weights w Evaluate on unseen test set

Lexical Generation GENLEX Input Training Example • Input: a training example ( x i ,z i ) Sentence: � Texas borders Kansas � Logic Form: � borders ( texas,kansas ) • Computation: Output Lexicon 1. Create all substrings of words in x i Words Category 2. Create categories from logical form z i Texas NP : texas 3. Create lexical entries that are the cross product of these two sets borders (S\NP)/NP : � x. � y.borders ( y,x ) • Output: Lexicon � Kansas NP : kansas ... ... Step 1: GENLEX Words Step 2: GENLEX Categories Input Logical Form: Input Sentence: borders(texas,kansas) Texas borders Kansas Output Categories: Ouput Substrings: ... Texas borders ... Kansas ... Texas borders borders Kansas Texas borders Kansas

Two GENLEX Rules All of the Category Rules Input Trigger Output Category Input Trigger Output Category a constant c NP : c arity one predicate p N : � x.p ( x ) a constant c NP : c arity one predicate p S\NP : � x.p ( x ) an arity two predicate p (S\NP)/NP : � x. � y.p ( y,x ) arity two predicate p (S\NP)/NP : � x. � y.p ( y,x ) arity two predicate p (S\NP)/NP : � x. � y.p ( x,y ) Example Input: � borders(texas,kansas) arity one predicate p N/N : � g. � x.p ( x ) � g(x) Output Categories: arity two predicate p N/N : � g. � x.p ( x,c ) � g(x) and constant c NP : texas NP : kansas � � arity two predicate p (N\N)/NP : � x. � g. � y.p ( y,x ) � g(x) (S\NP)/NP : � x. � y.borders ( y,x ) arity one function f NP/N : � g.argmax/min(g(x), � x.f(x)) arity one function f S/NP : � x.f(x) Step 3: GENLEX Cross Product GENLEX: Output Lexicon Input Training Example Words Category Sentence: � Texas borders Kansas � Texas NP : texas Logic Form: � borders ( texas,kansas ) Texas NP : kansas Texas (S\NP)/NP : � x. � y.borders ( y,x ) Output Lexicon borders NP : texas Output Substrings: Output Categories: � borders NP : kansas Texas borders (S\NP)/NP : � x. � y.borders ( y,x ) borders NP : texas X ... ... Kansas NP : kansas Texas borders Kansas NP : texas Texas borders (S\NP)/NP : � x. � y.borders ( x , y ) borders Kansas Texas borders Kansas NP : kansas Texas borders Kansas Texas borders Kansas (S\NP)/NP : � x. � y.borders ( y,x ) GENLEX is the cross product in these two output sets