Machine Learning for Computational Linguistics May 3, 2016 - PDF document

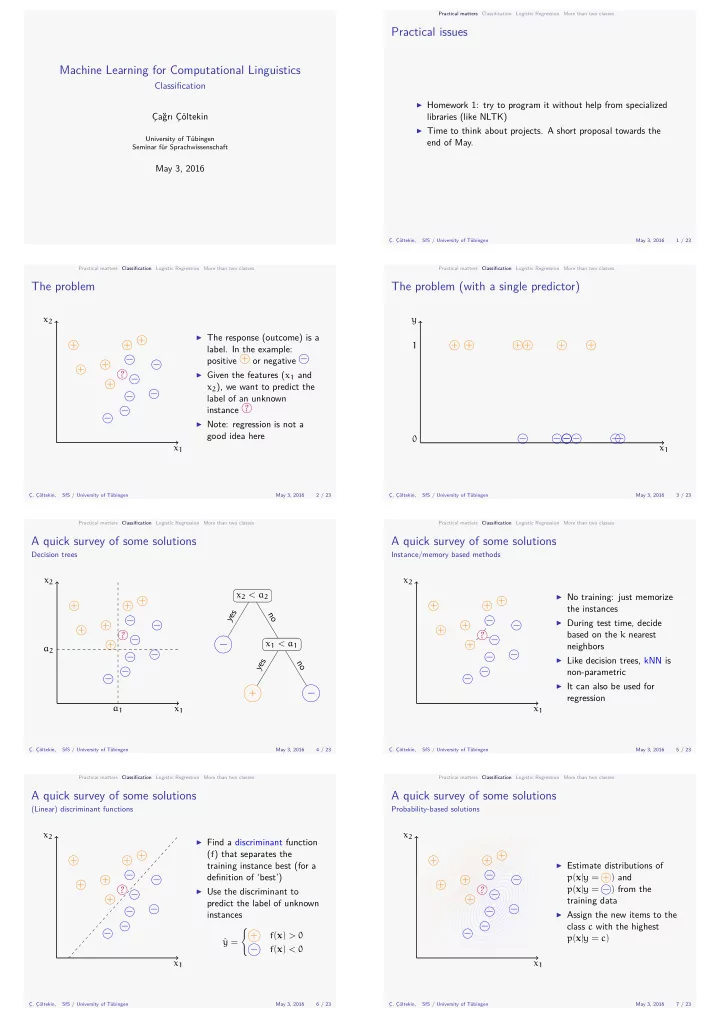
Machine Learning for Computational Linguistics May 3, 2016 regression non-parametric neighbors the instances Instance/memory based methods A quick survey of some solutions More than two classes Logistic Regression Classifjcation Practical matters 4 / 23 Classifjcation SfS / University of Tübingen Ç. Çöltekin, Decision trees A quick survey of some solutions More than two classes Logistic Regression Classifjcation Practical matters 3 / 23 May 3, 2016 SfS / University of Tübingen Ç. Çöltekin, Ç. Çöltekin, May 3, 2016 More than two classes May 3, 2016 May 3, 2016 SfS / University of Tübingen Ç. Çöltekin, training data Probability-based solutions A quick survey of some solutions More than two classes Logistic Regression Classifjcation Practical matters 6 / 23 SfS / University of Tübingen 5 / 23 Ç. Çöltekin, instances predict the label of unknown defjnition of ‘best’) training instance best (for a (Linear) discriminant functions A quick survey of some solutions More than two classes Logistic Regression Classifjcation Practical matters The problem (with a single predictor) SfS / University of Tübingen Logistic Regression end of May. The problem More than two classes Logistic Regression Classifjcation Practical matters 1 / 23 May 3, 2016 SfS / University of Tübingen Ç. Çöltekin, libraries (like NLTK) label. In the example: Practical issues More than two classes Logistic Regression Classifjcation Practical matters May 3, 2016 Seminar für Sprachwissenschaft University of Tübingen Çağrı Çöltekin Classifjcation 7 / 23 label of an unknown Ç. Çöltekin, Practical matters 2 / 23 May 3, 2016 SfS / University of Tübingen good idea here ▶ Homework 1: try to program it without help from specialized ▶ Time to think about projects. A short proposal towards the x 2 y + ▶ The response (outcome) is a + + + + + + + + 1 positive + or negative − − + − + ? ▶ Given the features ( x 1 and − + x 2 ), we want to predict the − − instance ? − − ▶ Note: regression is not a − − − − − − 0 x 1 x 1 x 2 x 2 x 2 < a 2 ▶ No training: just memorize + + + + + + yes no − − + − + − ▶ During test time, decide + + based on the k nearest ? ? − − − x 1 < a 1 + + a 2 − − − − ▶ Like decision trees, kNN is yes no − − − − ▶ It can also be used for + − a 1 x 1 x 1 x 2 x 2 ▶ Find a discriminant function + ( f ) that separates the + + + + + ▶ Estimate distributions of − − p ( x | y = +) and + − + − + + p ( x | y = −) from the ? ? − ▶ Use the discriminant to − + + − − − − ▶ Assign the new items to the − − class c with the highest { − − + f ( x ) > 0 p ( x | y = c ) ˆ y = − f ( x ) < 0 x 1 x 1

Practical matters 0.2 12 / 23 Practical matters Classifjcation Logistic Regression More than two classes Logit function 0.0 0.4 SfS / University of Tübingen 0.6 0.8 1.0 -4 -2 0 2 May 3, 2016 Ç. Çöltekin, p distributed normally 1 2 Test score P(dyslexia|score) Problems: are not bounded for correct predictions Ç. Çöltekin, function, with some ambiguity). SfS / University of Tübingen Classifjcation 11 / 23 Practical matters Classifjcation Logistic Regression More than two classes Example: transforming the output variable 4 logit(p) -1 More than two classes Ç. Çöltekin, SfS / University of Tübingen May 3, 2016 14 / 23 Practical matters Classifjcation Logistic Regression Logistic regression as a generalized linear model x Logistic regression is a special case of generalized linear models (GLM). GLMs are expressed with, family distributed binomially distributed normally Ç. Çöltekin, SfS / University of Tübingen May 3, 2016 logistic(x) 1.0 Ç. Çöltekin, Logit function SfS / University of Tübingen May 3, 2016 13 / 23 Practical matters Classifjcation Logistic Regression More than two classes -4 0.8 -2 0 2 4 0.0 0.2 0.4 0.6 0 May 3, 2016 100 simplifjed problem: Classifjcation Logistic Regression More than two classes A simple example 80 not based on a test applied to pre-verbal children. Here is a Test score 9 / 23 Dyslexia 82 0 22 1 62 1 Practical matters May 3, 2016 . 8 / 23 Logistic Regression More than two classes A quick survey of some solutions Artifjcial neural networks Ç. Çöltekin, SfS / University of Tübingen May 3, 2016 Practical matters SfS / University of Tübingen Classifjcation Logistic Regression More than two classes Logistic regression regression. It is a member of the family of models called generalized linear models Ç. Çöltekin, . We would like to guess whether a child would develop dyslexia or 15 / 23 . More than two classes Logistic Regression Classifjcation Practical matters 10 / 23 May 3, 2016 SfS / University of Tübingen Ç. Çöltekin, * The research question is from a real study by Ben Maasen and his colleagues. Data is fake as usual. . . . Example: fjtting ordinary least squares regression 60 40 20 0 x 2 + + + ▶ Logistic regression is a classifjcation method − ▶ In logistic regression, we fjt a model that predicts P ( y | x ) + − + x 1 ? ▶ Alternatively, logistic regression is an extension of linear − + y − − x 2 − − x 1 ▶ We test children when they are less than 2 years of age. ▶ The probability values ▶ We want to predict the diagnosis from the test score ▶ The data looks like between 0 and 1 ▶ Residuals will be large ▶ Residuals are not Instead of predicting the probability p , we predict logit(p) p logit ( p ) = log 1 − p p ˆ y = logit ( p ) = log 1 − p = w 0 + w 1 x p 1 − p (odds) is bounded between 0 and ∞ ▶ p ▶ log 1 − p (log odds) is bounded between − ∞ and ∞ ▶ we can estimate logit ( p ) with regression, and convert it to a probability using the inverse of logit e w 0 + w 1 x 1 p = ˆ 1 + e w 0 + w 1 x = 1 + e − w 0 − w 1 x which is called logistic function (or sometimes sigmoid 1 logistic ( x ) = 1 − e − x g ( y ) = Xw + ϵ ▶ The function g () is called the link function ▶ ϵ is distributed according to a distribution from exponential ▶ For logistic regression, g () is the logit function, ϵ is ▶ For linear regression g () is the identity function, ϵ is