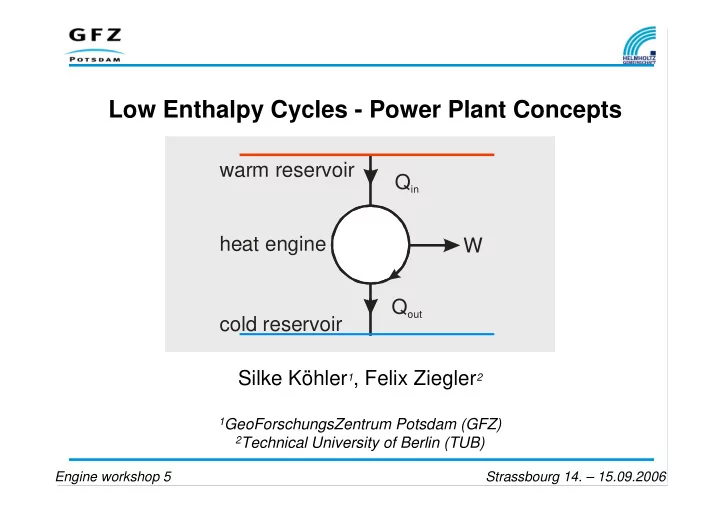

Low Enthalpy Cycles - Power Plant Concepts warm reservoir Q in heat engine W Q out cold reservoir Silke Köhler 1 , Felix Ziegler 2 1 GeoForschungsZentrum Potsdam (GFZ) 2 Technical University of Berlin (TUB) Engine workshop 5 Strassbourg 14. – 15.09.2006
Situation Heat source � Temperature 100°C – 200°C � Mass flow rate heat source 50 – 200 m³/h (~14 – 55 kg/s) � Limited heat capacity temperature cyclic ~ 5 to 50 MW th per well process � Sensible heat Goal: Electricity generation Tools heat sink � Cycles and systems � Design and optimisation entropy � Suitability of different cycles for particular applications
Optimisation of Ideal (Reversible) Cycles Internally and externally reversible � Carnot Cycle � Lorentz Cycle � Triangular Cycle Internally reversible � Rankine Cycle - ideal cycle for steam power processes Optimisation of the cycle locates the operating conditions for the optimal ideal cycle performance (Tamm et.al.)! Optimisation approach: � Locate constraints T, p � Locate free variables � Define optimisation criterium � objective function � Find Max / Min by analytical or numerical solving of the function
Carnot Cycle ∫ = Tds � q q in : A A23B � added heat q in : A A23B 2 3 � rejected heat q out : A A14B temperature ∫ = − = � w q q Tds in out � Net Work w: area A 1234 � Thermal efficiency η: 1 4 A 1234 area ratio q out : A A14B A A23B A B entropy
Optimisation of Carnot Cycle Constraints q η = − out 1 � Brine temperature, q in heat source mass flow rate ∫ = − = w q q Tds � Heat sink temperature in out T q , b r in , Free variable Carnot temperature cycle � Upper process temperature T e Possible objective functions � Thermal efficiency η � Net Work w heat sink � Added heat q in / Cooling of the brine T b,r entropy
Optimisation of Carnot Cycle η ↑ heat source heat source heat source w ↓ Carnot temperature temperature temperature T b,r ↑ cycle heat sink heat sink heat sink entropy entropy entropy η ↓ heat source heat source heat source w ↓ Carnot temperature temperature temperature T b,r ↓ cycle heat sink heat sink heat sink entropy entropy entropy
Optimisation of Carnot Cycle Constraints q η = − u 1 � Brine temperature, q o heat source mass flow rate ∫ ∫ = − = = − = w q q Tds w q q Tds � Heat sink temperature o u o u Free variable T q , b out o , Carnot temperature � Upper process cycle temperature Possible objective functions � Thermal efficiency η � Net Work w heat sink � Cooling of the brine T b,r entropy
Lorentz Cycle Constraints � Brine temperature, mass heat source flow rate � Heat sink temperature Free variable temperature temperature � Upper process temperature T e Possible objective functions � Thermal efficiency η � Net Work w heat sink � Added heat q in / Cooling of the brine T b,r entropy entropy
Optimisation of Lorentz Cycle η ↑ heat source heat source heat source w ↓ temperature temperature temperature T b,r ↑ heat sink heat sink heat sink entropy entropy entropy η ↓ heat source heat source heat source w ↓ temperature temperature temperature T b,r ↓ heat sink heat sink heat sink entropy entropy entropy
Reversible Triangular Cycle Fits in heat source / heat sink characteristics heat source No optimisation Availability? – not all state temperature changes can be realized with available hard ware Ideal cycles help to analyse complex heat sink problems Real cycles suffer losses entropy
Rankine Cycle (Organic Working Fluid) 1 2 isentropic compression 2 4 constant pressure heat addition preheater, evaporator KP 4 5 isentropic expansion p u p l 5 1 constant pressure heat rejection desuper- heater, condenser T e 3 4 temperature 5 2 T c 1 6 entropy
Actual Vapor Power Cycle (Organic Working Fluid) 1 2 irreversibility in the pump 2 3 pressure drop KP 3 4 pressure drop p u p l 4 5 irreversibility in the turbine 5 6 pressure drop 6 1 pressure drop T e 3 4 temperature 5 2 ideal cycle T c 1 real cycle 6 entropy
real cycle Irreversible Heat Transfer D T out T e D T in entropy T c temperature
ORC Layout evaporator turbine generator 4 G 3 preheater heat sink down 5 hole 2 pump 1 production injection feed condenser cooling well well pump water pump
Heat Transfer Diagram ORC Constraints � Brine: T b,in , mass flow rate, T b,in specific heat capacity e � Cooling medium: T CW,in , n i r b T CW,out , specific heat capacity D T min,in T e 4 3 temperature T b,out Free variables � Working fluid 5 � T e � ∆ T min,in , ∆ T min,out T c 1 6 2 D T min,out Objective function T CW,out T CW,in cooling water � Generator capacity Q out Q in � Heat transfer area transferred heat � (Ratio heat transfer area / generator capacity, ~ €/kW)
Kalina KCS 34 Layout 6’’ turbine generator desorber 6 G separator 7 5 6’ 8 9 10 pre- heater LT-recuperator 3 heat 4 4 sink HT- recuperator down 11 hole pump 2 1 production injection absorber cooling water feed well well pump pump basic solution rich vapor poor solution
Heat Transfer Diagram Kalina T b,in D T min,in 6’ 6 brine desorber temperature D T min,in T b,out 8 5 10 preheater 4 11 HT-preheater 3 absorber LT- preheater 1 D T min,out T CW,out cooling water T CW,in Q re Q out Q in transferred heat
Heat Transfer Diagram Kalina Constraints � Brine: T b,in , mass flow rate, T b,in specific heat capacity D T min,in 6 6’ � Cooling medium: T CW,in , T CW,out , specific heat capacity brine Free variables desorber temperature D T min,in T b,out � Composition basic solution 8 5 � Pressure desorption 10 preheater 4 � Pressure absorption & 11 HT-preheater � Q des 3 � Mass flow rate basic solution absorber & LT- preheater � Q 1 re 2 D T min,out T CW,out cooling water T CW,in Objective function Q out Q re Q in � Generator capacity transferred heat � Heat transfer area � (Ratio heat transfer area / generator capacity, ~ €/kW)
Return Temperature Brine, ORC & Kalina Optimised for work output 125 125 ORC Kalina return temperature brine (°C) 100 return temperature brine (°C) 100 75 75 50 50 25 25 air cooling air cooling water cooling water cooling 0 - 100°C 125°C 150°C 175°C 200°C 100°C 125°C 150°C 175°C 200°C (R290) (RC318) (R600a) (R600) (i-C5) initial temperature brine initial temperature brine, (working fluid)
Overall Efficiency ORC & Kalina Optimised for work output 10% 10% Kalina ORC 8% 8% overall efficiency overall efficiency 6% 6% 4% 4% 2% 2% air cooling air cooling water cooling water cooling 0% 0% 100°C 125°C 150°C 175°C 200°C 100°C 125°C 150°C 175°C 200°C (R290) (RC318) (R600a) (R600) (i-C5) initial temperature brine initial temperature brine, (working fluid) − − − P P P P P η = = gen DHpump FeedPump CWpump net ( ) & − sys & m c T T Q brine b b in brine , 0
Conclusions of Comparison Both systems are suitable for power production from low enthalpy reservoirs With given constraints from heat source and heat sink � ORC cool the brine more � Kalina reach higher thermal efficiency � High parasitic loads at ORC, especially for air cooling � ORC are more sensible to changes ORC of heat sink Suitability of the systems � Kalina KCS34 up to 150 ° C brine or CHP � ORC from 150 ° C brine temperature Improvements � Supercritical ORC may improve thermal efficiency � Other Kalina systems may improve cooling of brine
Geothermal Heat and Power Serial Parallel electrical waste heat energy electrical heat to district waste heat energy heating system power plant T power plant heating station T brine brine out T brine brine out s s Q H heating station T � brine temperature > temperature for heating purposes Q H � Not necessarily simultaneous heat to district heating system production � brine temperature ≈ temperature for heating Additional constraints due to � Subsystems compete heating demand! � Outlet temperature brine � Mass flow rate brine
Neustadt-Glewe Constraints � Brine temperature, net capacity to grid mass flow rate power plant � Heat sink temperature T generator capacity T b,out 210 kW el � Heating capacity in district heating system brine 98°C Free variable s 110 m³/h � Portion of brine through plant / upper process temperature heating station 6 MW geothermal Objective functions th 11 MW total th � Generator capacity ~ P mech � Cooling of the brine T b,out � Resource Utilization Factor heat to district heating system RUE (overall exergetic efficiency) ( ( ) ) − + ⋅ − − ⋅ − & P P m h h T s s exergy products RUE = = t p heatingsys tem HS HS HS HS , 0 0 , 0 ( ( ) ) ⋅ − − ⋅ − & exergy brine m h h T s s brine in in 0 0 0
Recommend
More recommend