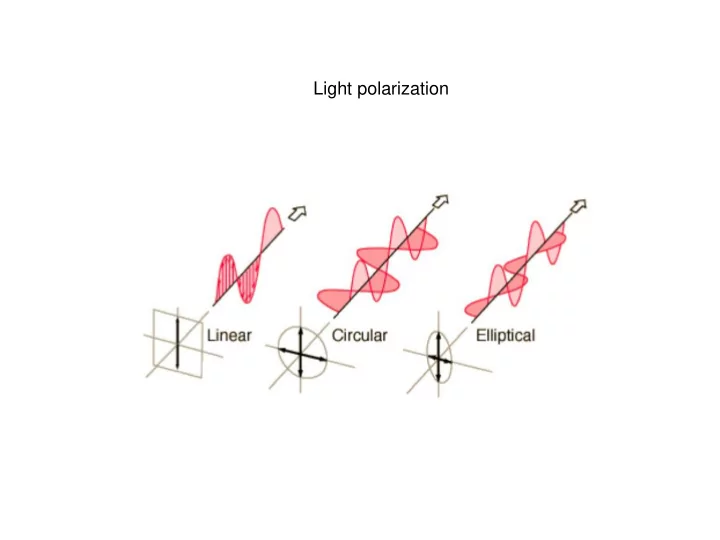
Light polarization nano@nanogune.eu I www.nanogune.eu - PowerPoint PPT Presentation

Light polarization nano@nanogune.eu I www.nanogune.eu nano@nanogune.eu I www.nanogune.eu

Jones vectors and matrices Since light is composed of oscillating electric and magnetic fields, Jones reasoned that the most natural way to represent light is in terms of the electric field vector. When written as a column vector, this vector is known as a Jones vector and has the form: These values can be complex numbers, so both amplitude and phase information is present. Oftentimes, however, it is not necessary to know the exact amplitudes and phases of the vector components. Therefore Jones vectors can be normalized and common phase factors can be neglected. TM or p TE or s Horizontal and vertical linear polarization states (reflection plane xz). nano@nanogune.eu I www.nanogune.eu nano@nanogune.eu I www.nanogune.eu

Normalized representation Linearly polarized light at 45 ° Right-circular polarized light - y E x E x t E y y E x Left-circular polarized light nano@nanogune.eu I www.nanogune.eu nano@nanogune.eu I www.nanogune.eu

Normalized representation Elliptically polarized light   1     E 1 ~   = = E = ox E     oy  e i   o       E e i be i   oy E ox y E oy b = e 2 /e 1   e 2 2 E E cos 2 b cos ox oy q = = tan 2 K − − 2 2 2 E E 1 b ox oy q K   2 E E sin e 1 2 b sin ox oy  = = sin 2 x K + + 2 2 2 E E 1 b E ox ox oy nano@nanogune.eu I www.nanogune.eu nano@nanogune.eu I www.nanogune.eu

To model the effect of a medium on light's polarization state, we use Jones matrices. Since we can write a polarization state as a (Jones) vector, we use matrices, A , to transform them from the input polarization, E 0 , to the ~ ~ output polarization, E 1 . = A ~ E E 1 0   = + a a E a E a E This yields: = 11 12 1 x 11 0 x 12 0 y A     = + a a E a E a E 21 22 1 y 21 0 x 22 0 y   1 0 =  A  For example, an x-polarizer can be written: x   0 0       E 1 0 E So: = = = 0 x 0 x   E A E     1 x 0   E   0 0   0 0 y nano@nanogune.eu I www.nanogune.eu nano@nanogune.eu I www.nanogune.eu

Other Jones matrices   0 0 =  A y-polarizer: A  y   0 1         A half-wave plate: 1 0 1 0 1 1 =  = A        − − − HWP         0 1 0 1 1 1       1 0 1 1 A half-wave plate rotates 45-degree- =       polarization to -45-degree, and vice − −       0 1 1 1 versa. A quarter-wave plate:         1 0 1 0 1 1 =  = A           QWP         0 i 0 i 1 i nano@nanogune.eu I www.nanogune.eu nano@nanogune.eu I www.nanogune.eu

A wave plate is not a wave plate if it’s oriented wrong. 0 ° or 90 ° Polarizer Remember that a wave plate wants ± 45 ° (or circular) polarization. Wave plate w/ axes at If it sees, say, x polarization, 0 ° or 90 ° nothing happens.       1 0 1 1 =       −       0 1 0 0 A HWP So use Jones matrices until you’re really on top of this!!! nano@nanogune.eu I www.nanogune.eu nano@nanogune.eu I www.nanogune.eu

Summary Retardation l /4 Retardation l /4 −1 0 Retardation l /2 1 0 Half-wave plate, Half-wave plate, Retardation l /2 fast axis vertical 0 1 fast axis horizontal 0 −1 1 0 In terms of waves (wavelength l ), General retarder, this is a retarder l * j /2 p 𝑓 𝑗𝜒 fast axis horizontal 0 nano@nanogune.eu I www.nanogune.eu nano@nanogune.eu I www.nanogune.eu

Rotated Jones matrices Okay, so E 1 = A E 0 . What about when the polarizer or wave plate responsible for A is rotated by some angle, q ? Rotation of a vector by an angle q means multiplication by a rotation matrix: ( ) ( ) = q = q E ' R E and E ' R E 0 0 1 1 where: q − q   cos( ) sin( ) ( ) q =   R q q   sin( ) cos( ) Rotating E 1 by q and inserting the identity matrix R ( q ) -1 R ( q ) , we have: ( ) ( ) ( )  ( ) ( )  − = q = q = q q 1 q E ' R E R A E R A R R E   1 1 0 0 ( ) ( ) ( ) ( ) ( )  −   −  = q q  q  = q q = 1 1 R A R R E R A R E ' A ' E '       0 0 0 Thus: ( ) ( ) − = q q 1 A ' R A R nano@nanogune.eu I www.nanogune.eu nano@nanogune.eu I www.nanogune.eu

Rotated Jones matrix for a polarizer ( ) ( ) − Applying this result to an x-polarizer: = q q 1 A ' R A R q − q q q       cos( ) sin( ) 1 0 cos( ) sin( ) ( ) q =  A      q q − q q x       sin( ) cos( ) 0 0 sin( ) cos( ) q − q q q     cos( ) sin( ) cos( ) sin( ) ( ) q =  A    q q x     sin( ) cos( ) 0 0   q q q 2 cos ( ) cos( )sin( ) ( ) q =   A q q q x 2   cos( )sin( ) sin ( )      ( ) 1/ 2 1/ 2 1 ( ) for small =     A 45  A  angles,   x x     1/ 2 1/ 2 0 nano@nanogune.eu I www.nanogune.eu nano@nanogune.eu I www.nanogune.eu

Jones Matrices for standard components nano@nanogune.eu I www.nanogune.eu nano@nanogune.eu I www.nanogune.eu

To model the effect of many media on light's polarization state, we use many Jones matrices. To model the effects of more than one component on the polarization state, just multiply the input polarization Jones vector by all of the Jones matrices: = A A A E E 1 3 2 1 0 A single Jones matrix (the product of the individual Jones matrices) can describe Remember to use the correct order! the combination of several components. nano@nanogune.eu I www.nanogune.eu nano@nanogune.eu I www.nanogune.eu

x Multiplying Jones Matrices z y Crossed polarizers: x-pol E 0 E = A A E E 1 1 y x 0 y-pol       0 0 1 0 0 0 = = A A       so no light leaks through. y x       0 1 0 0 0 0 rotated x-pol Uncrossed polarizers E E (slightly): 0 1        y-pol 0 0 1 0 0 ( )  = = A A         y x       0 1 0 0         E E 0 0 0 ( ) So I out ≈  2 I in,x  = = x x     A A       y x   E E     0   E y y x nano@nanogune.eu I www.nanogune.eu nano@nanogune.eu I www.nanogune.eu

The MagnetoOptical Effect p Reflected Light p z s s z θ Polarization Plane s θ θ p s p x p Sample x y s Transmitted Light Dielectric tensor    −    x =  0 Q m x    i i 0 0 M 0 z y 0      y =  0 Q m y  = −     =  ˆ ˆ 0 0  i i    0 z 0 x  z =  0 Q m z ;       −     0 0 i i   0 y x 0 Fresnell reflection coefficients M             E E 0 E r E r r     rp         ip pp ip pp ps rp = =               r r   0 r       E E E E sp ss ss rs is is rs E E E E r = r = r = r = rTM rTE rTE rTM sp pp ss ps E E E nano@nanogune.eu I www.nanogune.eu nano@nanogune.eu I www.nanogune.eu E iTM iTM iTE iTE

The MagnetoOptical Effect general case: Oblique incidence and arbitrary direction of M   r r   pp ps   r r   sp ss − q n 2 n 2 n 2 sin 2 q = − q = − q = 0 1 0 cos 1 sin 1 sin 2 2 1 1 n n 2 1 1 M  m y  xy = i  1 Q m z ;  xz = -i  1 Q m y ;  yz = i  1 Q m x ; r pp = r 0 pp + r pp  - m x - m z r ps  xy = -  yx ;  zx = -  xz ;  zy = -  yz ;  m x -m z r sp nano@nanogune.eu I www.nanogune.eu nano@nanogune.eu I www.nanogune.eu

MOKE configurations nano@nanogune.eu I www.nanogune.eu nano@nanogune.eu I www.nanogune.eu