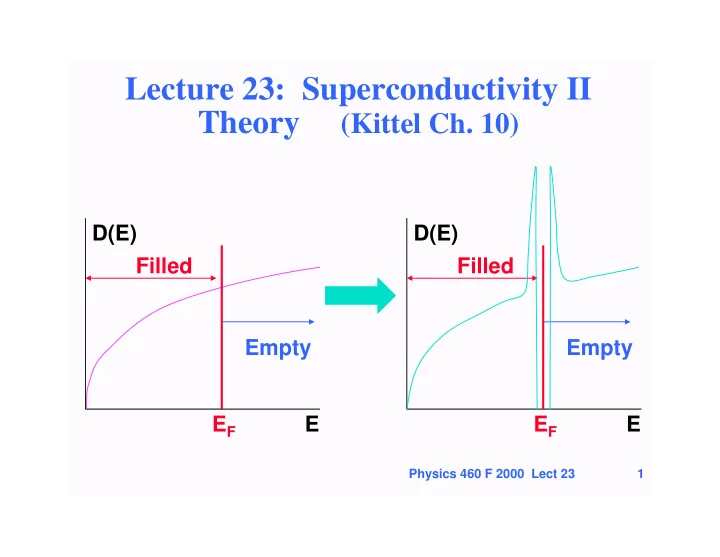

Lecture 23: Superconductivity II Theory (Kittel Ch. 10) D(E) D(E) Filled Filled Empty Empty E F E E F E Physics 460 F 2000 Lect 23 1
Outline • Superconductivity - Concepts and Theory • Key points Exclusion of magnetic fields can be used to derive energy of the superconducting state Heat Capacity shows there is a gap Isotope effect • How does a superconductor exclude B field? London penetration depth (1930’s) • Flux Quantization How we know currents are persistent! • Cooper instability - electron pairs Bardeen, Cooper, Schrieffer theory (1957) (Nobel Prize for work done in UIUC Physics) • (Kittel Ch 10 ) Physics 460 F 2000 Lect 23 2
Meisner Effect • Magnetic field B is excluded B = H + µ 0 M • For type I superconductors, µ 0 M = - H for T < T c • Perfect Diamagnetism ! - µ 0 M B Super- Super- conducting conducting Normal Normal H c H H c H Physics 460 F 2000 Lect 23 3 From previous lecture
Meisner Effect (1934) • A superconductor can actively push out a magnetic field - Meisner effect • (For H < H c in type I superconductors and H < H c1 in type II superconductors) Excludes Magnetic Field Zero Field Cooled Field Cooled H H 0 0 T > T c T < T c T > T c T < T c Physics 460 F 2000 Lect 23 4 From previous lecture
Effect of a Magnetic Field • Magnetic fields tend to destroy superconductivity Note: H = external applied field B = internal field B = H + µ 0 M M = Magnetization H Phase Transition H c SUPERCONDUCTING Normal STATE IS A NEW PHASE OF MATTER Super- conducting T T c Physics 460 F 2000 Lect 23 5 From previous lecture
Energy : normal vs. superconducting • The free energy F of the superconductor plus magnetic field is increased because magnetic field B is excluded • The normal state energy is nearly independent of field • Transition at H c Superconducting F S (H) = F S (0) + H 2 /2 µ 0 F F N Normal F S (0) H c H Physics 460 F 2000 Lect 23 6
Energy : normal vs. superconducting 2 /2 µ 0 = F N (0) • Therefore F S (H c ) = F S (0) + H c ∆ F = F N (0) - F S (0) = H c 2 /2 µ 0 or • Typical Values: ∆ F ~ 10 -7 eV/electron ! SMALL ! Superconduc. F S (H) = F F S (0) + H 2 /2m 0 F N Normal F S (0) H c H Physics 460 F 2000 Lect 23 7
Energy : normal vs. superconducting • How do we understand the small values ∆ F ~ 10 -7 eV/electron ? • Similar to the description of thermal energy ∆ F ~ D(E F ) ∆ E 2 ~ ∆ k 2 where ∆ E is the region affected - as shown by the gap in the heat capacity - agrees with experiment D(E) Filled k F ∆ E ∆ k Empty E F E Physics 460 F 2000 Lect 23 8
Coherence Length • The typical length associated with the mechanism of superconductivity is the feature associated with ξ = 1/ ∆ k = hv F /2 ∆ E the Fermi surface is where ∆ E is the region affected (Understood from the BCS theory – see later) Typical values ξ = 1,600 nm Al T c = 1.19K ξ = 83 nm k F Pb T c = 7.18K ∆ k Physics 460 F 2000 Lect 23 9
How is a field excluded? • What makes B = 0 inside superonductor? • Supercurrents flowing on the boundary! • Easiest geometry - long thin rod B = 0 inside Current around boundary causes field inside that cancels the external field - H A supercurrent that flows with no decay Physics 460 F 2000 Lect 23 10
Thickness of region where current flows • Supercurrents J flowing on the boundary! Superconductor Normal state or vacuum Supercurrent Both B field and J decay into superconductor H H Physics 460 F 2000 Lect 23 11
Thickness of region where current flows Normal state Superconductor • London Penetration or vacuum Depth λ L • Maxwell’s Eq.: ∇ × B = µ 0 j ∇ × ∇ × B = - ∇ 2 B = µ 0 ∇ × j • Also B = ∇ × A (A not unique) • London PROPOSED Both B field that in the gauge and J decay into ∇ A = 0, A normal = 0, superconductor H 2 ) j = - A/( µ 0 λ L λ L so ∇ × j = - B /( µ 0 λ L 2 ) Physics 460 F 2000 Lect 23 12
London Equations • Here we give a derivation of the London equations that gives physical insight and the expression for the penetration depth λ L • The free energy for the system with a supercurrent and the penetrating B field is n s = superfluid density F = F 0 + E kin + E mag v(r) = velocity where E mag = ∫ d r B 2 /8 π and E kin = ∫ d r ½ mv 2 n s with j(r) = n s q v(r) • Using ∇ × B = µ 0 j we find F = F 0 + (1/8 π) ∫ d r [B(r) 2 + λ L 2 = ε 0 mc 2 /n s q 2 2 ( ∇ × B(r)) 2 ], where λ L • Varying the form of B(r) by adding δ B(r) the change δ F is δ F = (1/4 π) ∫ d r [B(r) δ B(r) + λ L 2 ( ∇ × B(r)) ( ∇ × δ B(r)) ] Integration 2 ∇ × ∇ × B(r)] δ B(r) = (1/4 π) ∫ d r [B(r) - λ L by parts • At the minimum, δ F = 0 for all possible δ B(r) which requires that 2 ∇ × ∇ × B(r) = B(r) + λ L 2 ∇ 2 B(r) = 0 B(r) - λ L • Which leads to the London Equation Physics 460 F 2000 Lect 23 13
Thickness of region where current flows Normal state Superconductor • Therefore or vacuum ∇ 2 B = B/ λ L 2 Solution: B decays into superconductor with the form B(x) = B(0) exp(-x/ λ L ) Both B field and J decay into • Explains Meisner effect superconductor H B vanishes inside the λ L superconductor Physics 460 F 2000 Lect 23 14
The superconducting state is a quantum state • Landau and Ginsburg (before the BCS theory) proposed all the electrons act together to form a new state Ψ, with | Ψ | 2 = n s where n s is the superfluid density 1/2 - No current flowing • Ground state: Ψ G = n s 1/2 ) exp( i θ (r)) - the phase in • Consider now Ψ = ( n s a wavefunction corresponds to a current • The velocity operator is v = p/m = (1/m)( - i h ∇ - (q/c)A) Thus j = q Ψ ∗ v Ψ = (n s q/m) (h ∇θ - (q/c)A) and curl j = - (n s q 2 /mc) B Physics 460 F 2000 Lect 23 15
The superconducting state is a quantum state - II • This quantum state leads to a theory of the London penetration depth • The equation curl j = - (n s q 2 /mc) B and the London proposal 2 ) curl j = - B /( µ 0 λ L See earlier slide leads to for alternative 2 = ε 0 mc 2 / n s q 2 λ L derivation • Agrees with experiment! BUT what is m? What is q? How do we really know it is quantum in nature? Physics 460 F 2000 Lect 23 16
Quantized Flux • The flux enclosed in a ring is quantized! • Consider a line inside the superconductor The current j = 0 inside • h ∇θ - (q/c)A = 0 inside the superconductor Magnetic field threading ring H Current only near surface Physics 460 F 2000 Lect 23 17
Quantized Flux -II • The line integral of ∇θ is the change in θ around the loop = 2 π x integer • The line integral of A is the surface integral of B (See Kittel p 281) = total flux Φ enclosed in the ring • Result: Φ = ( 2 π hc/q) x integer -- quantized! Line integral on a closed contour inside the superconductor • Result: Charge q = 2e - pairs ! Physics 460 F 2000 Lect 23 18
Persistent Currents • How can the current stop flowing? • Only if some of the flux Φ leaks out of the ring • But the flux can only decrease by quanta! • There is an energy barrier for the flux to go through the superconductor to escape - time for current to decrease can be ~ age of universe! Physics 460 F 2000 Lect 23 19
Two length scales in superconductivity • London Penetration depth 2 = ε 0 mc 2 /nq 2 (particles of mass m, charge q) λ L • (Understood from the BCS theory that m and q are for an electron pair – see later) Typical values Al T c = 1.19K ξ = 1,600 nm λ L = 160 nm ξ / λ L = 0.01 T c = 7.18K ξ = 83 nm λ L = 370 nm ξ / λ L = 0.45 Pb The ratio determines type I ( ξ / λ L <<1) and type II ( ξ / λ L > ~1) superconductors see later Other examples are given in Kittel Physics 460 F 2000 Lect 23 20
Type II • Type II superconductors are ones where it is favorable to break up the field into quanta - the smallest posible unit of flux in each “vortex” shown - for H c1 < H < H c2 • Lattice of quantized flux units H applied Magnetic flux penetrates through the superconductor by creating small regions normal metal Physics 460 F 2000 Lect 23 21
BCS theory • Hints: Must involve phonons, small energy scale • First: Cooper instability • If for some reason there were an attractive interaction between two electrons above the Fermi energy in a metal, they would form a bound pair below the Fermi energy no matter how weak the interaction! • Two electrons of k F opposite k and opposite spin form a bound state • Fermi surface is unstable! Physics 460 F 2000 Lect 23 22
BCS theory - II • What could cause the attraction? - phonons! • The Coulomb interaction is repulsive • But phonons can cause the “Mattress effect” - one electron causes the lattice to distort - the second electron is attracted the the distortion even after the first electron has left! • Two electrons of opposite k and opposite spin form a bound state! Physics 460 F 2000 Lect 23 23
BCS theory - III • The Cooper idea shows there is a problem for two electrons - but what do all the electrons do? • This is the key advance of BCS - to construct a new quantum wavefunction for all the electrons • Fundamental change only for electrons within a energy range ∆ E near the Fermi surface • Opens an energy gap - explains the specific heat • Forms single quantum state Ψ separated by a gap from other states Physics 460 F 2000 Lect 23 24
Recommend
More recommend