l l
play

L L 2 = + 0 1 t v v Detector 1 0 THE VESUVIO SPECTOMETER - PowerPoint PPT Presentation

May 10, 2023 •451 likes •641 views

Time of Flight Measurement Principle ( ) = 2 2 h 1 m v v L 0 0 1 2 ( ) = + 2 2 2 2 q m v v 2 v v cos 0 1 0 1 2 M q = L 1 y Moderator Sample q

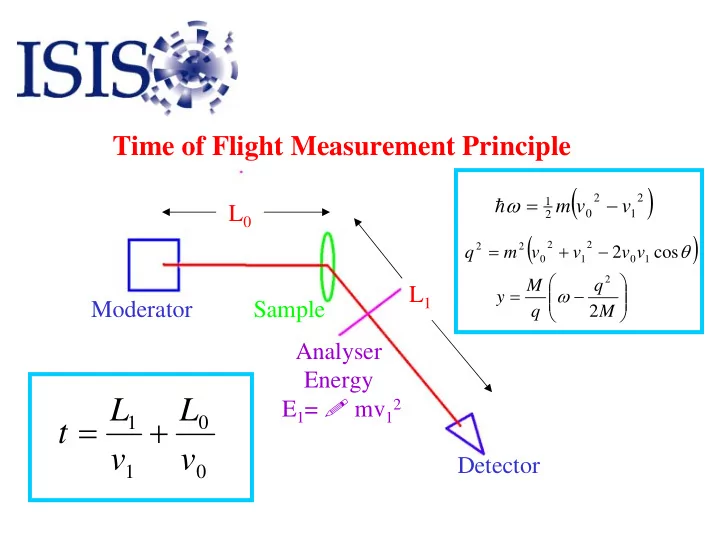
  1. Time of Flight Measurement Principle ( ) ω = − 2 2 h 1 m v v L 0 0 1 2 ( ) = + − θ 2 2 2 2 q m v v 2 v v cos 0 1 0 1   2 M q   = ω − L 1 y   Moderator Sample   q 2 M Analyser Energy E 1 = ! mv 1 L L 2 = + 0 1 t v v Detector 1 0

  2. THE VESUVIO SPECTOMETER

  3. The Filter Difference Method

  4. RESOLUTI ON COMPONENT ON VESUVI O • Geometrical component a a Gaussian • Energy component a a Gaussian and Lorentzian Au and U f oils U resonances: a a 6. 7 eV, 20. 7 eV, 37 eV • • FWHM (intrinsic width at 6. 7 eV) a a 0. 04 eV a a 0. 11 eV • Doppler broadning at RT a a 0. 06 eV • Doppler broadning at 70 K

  5. DOUBLE DIFFERENCE TECHNIQUE Gold Foil U Foil 1-e -Nt σ =Nt σ as σ→ 0

  6. Double Differenced and Single Differenced Pb Data taken with Au Foil

  7. Impulse Approximation r + r r p q p Momentum transfer r + r κ = κ = 2 2 ( p q ) / 2 M p / 2 M f i r r r   + 2 r 2 2 M q ( p q ) p   = = ω − ω = − ˆ y p . q     q 2 M 2 M 2 M ˆ Momentum along q Energy transfer

  8. Kinetic Energy of 4 He Potential Energy of 4 He

  9. Quantum Correlations in H 2 O/D 2 O Mixtures A Driesmann, et al PRL 79 2839 (1997)

  10. DI NS in H 2 S

  11. IMPULSE APPROXIMATION r M ω = Dynamic Structure Factor ˆ S ( q , ) J ( q , y ) q r r r r ∫ = δ − Radon Transform ˆ J ( q , y ) n ( p ) ( y p . q ) d p   2 M q   = ω − y   Longitudinal momentum component   q 2 M

  12. RADON TRANSFORM y r r r r ∫ = δ − ˆ J ( q , y ) n ( p ) ( y p . q ) d p

  13. Momentum Distribution is “Diffraction Pattern” of Wave function r r r r r 2 ∫ = ψ n ( p ) ( r ) exp( i p . r ) d r

  14. Reconstruction of Momentum Distribution from Neutron Compton Profile Hermite polynomial Spherical Harmonic − 2 exp( y ) ∑ = ˆ ˆ J ( q , y ) a H ( y ) Y ( q ) + π n , l , m 2 n l l , m n , l , m a n,l,m is Fitting coefficient − 2 r exp( p ∑ + + = − 2 n l n l l 1 / 2 2 ˆ n ( p ) 2 n ! ( 1 ) a p L ( p ) Y ( p ) π n , l , m n lm 3 / 2 n , l , m Laguerre polynomial

Recommend

More recommend