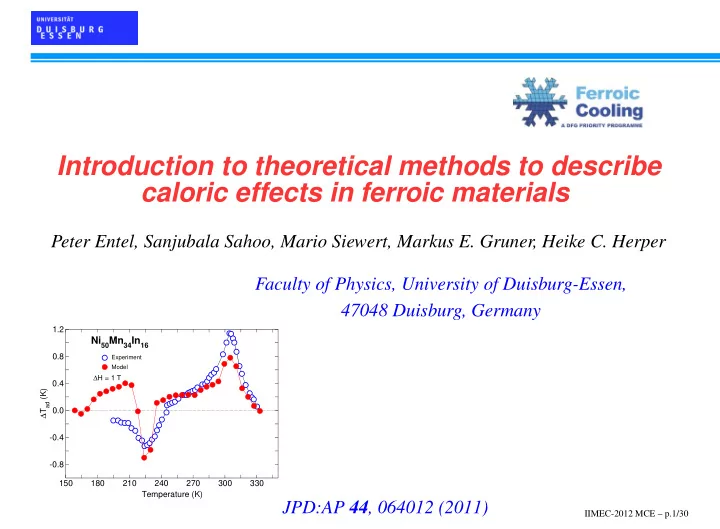

Introduction to theoretical methods to describe caloric effects in ferroic materials Peter Entel, Sanjubala Sahoo, Mario Siewert, Markus E. Gruner, Heike C. Herper Faculty of Physics, University of Duisburg-Essen, 47048 Duisburg, Germany 1.2 Ni 50 Mn 34 In 16 0.8 Experiment Model ∆ H = 1 T 0.4 ∆ T ad (K) 0.0 -0.4 -0.8 150 180 210 240 270 300 330 Temperature (K) JPD:AP 44 , 064012 (2011) IIMEC-2012 MCE – p.1/30
Motivation: Functional properties of Heuslers Interplay of magnetism and structural transformation: – Exchange bias (EB) effect: Shift of magnetic hysteresis curve – Magnetocaloric effect (MCE): Conventional (heating) and inverse (cooling) effect – Magnetic shape memory effect (MSME): Huge strain effect in the martensitic phase in an external magnetic field Origin: Competing ferro- and antiferromagnetic interactions IIMEC-2012 MCE – p.2/30
Introduction Solid state refrigeration can reduce the worldwide CO 2 emission Cooling requires to control the entropy of the refrigeration medium: (possible at phase transitions) Solid state refrigeration requires diffusionless transformation because diffusion is too slow IIMEC-2012 MCE – p.3/30
Introduction Solid state refrigeration can reduce the worldwide CO 2 emission Cooling requires to control the entropy of the refrigeration medium: (possible at phase transitions) Solid state refrigeration requires diffusionless transformation because diffusion is too slow S. Fähler et al., Adv. Eng. Mater. 13 , 1 (2011) L. Mañosa et al., Nat, Mater. 9 , 478 (2010) IIMEC-2012 MCE – p.3/30
Introduction Solid state refrigeration can reduce the worldwide CO 2 emission Cooling requires to control the entropy of the refrigeration medium: (possible at phase transitions) Solid state refrigeration requires diffusionless transformation because diffusion is too slow Barocaloric cooling cycle: Adiabatic compression of austenite in- duces martensite / twins and increases T Heat is releasesed to external reservoir Adiabatic decompression induces austen- ite and decreases T System is connected to cold reservoir be- coming colder S. Fähler et al., Adv. Eng. Mater. 13 , 1 (2011) L. Mañosa et al., Nat, Mater. 9 , 478 (2010) IIMEC-2012 MCE – p.3/30
Electrocaloric effect cooling cycle Cycle involving two constant-entropy transitions and two at constant field E IIMEC-2012 MCE – p.4/30
Electrocaloric effect cooling cycle Cycle involving two constant-entropy transitions and two at constant field E J. F . Scott., Annu. Rev. Res. 41 , 229 (2011) Z. Zhao et al., Nat, Mater. 5 , 8233 (2006) IIMEC-2012 MCE – p.4/30
Electrocaloric effect cooling cycle Cycle involving two constant-entropy transitions and two at constant field E Electrocaloric cooling cycle: (a) Initial state T - E is rapidly applied bringing the crystal to lower entropy (b) At higher T - subsequently the crystal is allowed to cool at constant E lowering entropy to (c) (c) E is reduced to 0 and further cooling by adiabatic depolarization (d) System warms up to J. F . Scott., Annu. Rev. Res. 41 , 229 (2011) initial state absorbing Z. Zhao et al., Nat, Mater. 5 , 8233 (2006) heat from the local IIMEC-2012 MCE – p.4/30
Electrocaloric entropy change Calculated entropy S(T) of BaTiO 3 : IIMEC-2012 MCE – p.5/30
Electrocaloric entropy change Calculated entropy S(T) of BaTiO 3 : H.-X. Cao et al., J. Appl. Phys. 106 , 094104 (2009) ∆ T (model calculation) is of the order of 10 K IIMEC-2012 MCE – p.5/30
Electrocaloric entropy change Calculated entropy S(T) of BaTiO 3 : H.-X. Cao et al., J. Appl. Phys. 106 , 094104 (2009) ∆ T (model calculation) is of the order of 10 K IIMEC-2012 MCE – p.5/30
Caloric effects in ferroic materials Magnetocaloric effect (MCE): Magnetic materials change their thermodynamic properties like entropy and specific heat under the influence of a control parmeter: S(T, V, H, x, . . . ), C(T, V, H, x, . . . ) Effect known since 1880: E. Warburg, Ann. Phys. 13 , 131 (1881) Last decade: Materials which work at ambient temperature MCE: ∆ S ( T, H ) ≈ 10 J/(kg K), ∆ T ad ( T, H ) ≈ 1 − 10 K Challenge: How can one improve “systematically” the caloric effect? Issue: Strong interaction of experimental and theoretical groups Reviews: A.M. Tishin & Y.I. Spichkin (IOP , Bristol, 2003) The Magnetocaloric Effect and its Applications N.A. de Oliveira & P .J. von Ranke, Phys. Rep. 489 , 89 (2010) Theoretical aspects of the magnetocaloric effect V.D. Buchelnikov & V.V. Sokolovskii, Phys. Met. Metallogr. 112 , 633 (2011) Magnetocaloric effect in Ni-Mn-X (X = Ga, In, Sn, Sb) Heusler alloys IIMEC-2012 MCE – p.6/30
Giant MCE Materials 1990 FeRh Nikitin et al. 1997 Gd 5 (Ge 1 − x Si x ) 4 Pecharsky & Gschneidner 1998 RCo 2 Foldeaki et al. 2000-2002 La(Fe, Si) 13 Hu et al., Fukamichi et al. 2001 MnAs 1 − x Sb x Wada et al. 2002 MnFe(P , As) Tegus et al. 2003 Co(S 1 − x Se x ) 2 Yamada & Goto 2005 Ni 2 Mn 1+ x In 1 − x Krenke et al. 2009 MnCoGeB Trung et al. Complex crystalline and magnetic structures & “magnetostructural” phase transformations IIMEC-2012 MCE – p.7/30
Example of magnetostructural transition Valence electron number/atom ( e / a ) Valence electron number/atom ( e / a ) 7.50 7.55 7.60 7.65 7.70 7.75 7.80 7.50 7.55 7.60 7.65 7.70 7.75 7.80 270 P (L2 1 ) 600 600 600 600 Ni 2+x Mn 1-x Ga Ni 2+x Mn 1-x Ga Ni 2 MnGa 260 continuous 500 500 500 500 250 multicritical PM L2 1 PM PM L2 1 PM Temperature (K) Temperature (K) Temperature (K) point MCE T C T C martensite martensite 400 400 400 400 discontinuous X 240 discontinuous FM L2 1 FM L2 1 FM L2 1 FM L2 1 300 300 300 300 T I T I 230 M S M S 5M MSME 200 200 200 200 220 FM 5M, 7M FM L1 0 FM 5M, 7M FM L1 0 I (c/a < 1) (c/a > 1) (c/a < 1) (c/a > 1) 100 100 100 100 210 Phonon softening (TA 2 ) of P phase: precursor to the X-phase? FM non-modulated tetragonal martensite FM non-modulated tetragonal martensite 200 0 0 0 0 0 20 40 60 80 100 120 0.0 0.1 0.2 0.3 0.4 0.0 0.1 0.2 0.3 0.4 Compressive stress σ || [001] P (MPa) Ni excess (x) Ni excess (x) IIMEC-2012 MCE – p.8/30
Example of magnetostructural transition Valence electron number/atom ( e / a ) Valence electron number/atom ( e / a ) 7.50 7.55 7.60 7.65 7.70 7.75 7.80 7.50 7.55 7.60 7.65 7.70 7.75 7.80 270 P (L2 1 ) 600 600 600 600 Ni 2+x Mn 1-x Ga Ni 2+x Mn 1-x Ga Ni 2 MnGa 260 continuous 500 500 500 500 250 multicritical PM L2 1 PM PM L2 1 PM Temperature (K) Temperature (K) Temperature (K) point MCE T C T C martensite martensite 400 400 400 400 discontinuous X 240 discontinuous FM L2 1 FM L2 1 FM L2 1 FM L2 1 300 300 300 300 T I T I 230 M S M S 5M MSME 200 200 200 200 220 FM 5M, 7M FM L1 0 FM 5M, 7M FM L1 0 I (c/a < 1) (c/a > 1) (c/a < 1) (c/a > 1) 100 100 100 100 210 Phonon softening (TA 2 ) of P phase: precursor to the X-phase? FM non-modulated tetragonal martensite FM non-modulated tetragonal martensite 200 0 0 0 0 0 20 40 60 80 100 120 0.0 0.1 0.2 0.3 0.4 0.0 0.1 0.2 0.3 0.4 Compressive stress σ || [001] P (MPa) Ni excess (x) Ni excess (x) 23 50% Ni 48% Ni 46% Ni 44% Ni Ni 2-x Mn 1+x+y Ga 1-y 300 K 22 (e/a = 7.64) M S = 280 K (e/a = 7.61) Ga (at. %) 21 370 K (e/a = 7.74) 20 Tetragonal Ni 49 Mn 32 Ga 19 Mixed T C = 368, M S = 353 K Orthorhombic 19 Cubic / 5M 26 28 30 32 34 Mn (at. %) IIMEC-2012 MCE – p.8/30
Example of magnetostructural transition Valence electron number/atom ( e / a ) Valence electron number/atom ( e / a ) 7.50 7.55 7.60 7.65 7.70 7.75 7.80 7.50 7.55 7.60 7.65 7.70 7.75 7.80 270 P (L2 1 ) 600 600 600 600 Ni 2+x Mn 1-x Ga Ni 2+x Mn 1-x Ga Ni 2 MnGa 260 continuous 500 500 500 500 250 multicritical PM L2 1 PM PM L2 1 PM Temperature (K) Temperature (K) Temperature (K) point MCE T C T C martensite martensite 400 400 400 400 discontinuous X 240 discontinuous FM L2 1 FM L2 1 FM L2 1 FM L2 1 300 300 300 300 T I T I 230 M S M S 5M MSME 200 200 200 200 220 FM 5M, 7M FM L1 0 FM 5M, 7M FM L1 0 I (c/a < 1) (c/a > 1) (c/a < 1) (c/a > 1) 100 100 100 100 210 Phonon softening (TA 2 ) of P phase: precursor to the X-phase? FM non-modulated tetragonal martensite FM non-modulated tetragonal martensite 200 0 0 0 0 0 20 40 60 80 100 120 0.0 0.1 0.2 0.3 0.4 0.0 0.1 0.2 0.3 0.4 Compressive stress σ || [001] P (MPa) Ni excess (x) Ni excess (x) 23 50% Ni 48% Ni 46% Ni 44% Ni Ni 2-x Mn 1+x+y Ga 1-y 300 K 22 (e/a = 7.64) M S = 280 K (e/a = 7.61) Top: V. V. Khovaylo et al., PRB 72 , 224408 (2005) Ga (at. %) 21 370 K H. Kushida et al., Scripta Mater. 60 , 96 (2009) (e/a = 7.74) 20 Left: Tetragonal Ni 49 Mn 32 Ga 19 Mixed M. Richard et al., Scripta Mater. 54 , 1797 (2006) T C = 368, M S = 353 K Orthorhombic 19 Cubic / 5M 26 28 30 32 34 Mn (at. %) IIMEC-2012 MCE – p.8/30
Recommend
More recommend