
Improved fluid models for runaway generation and decay Ola Embr´ eus ul¨ Adam Stahl, Linnea Hesslow, T¨ unde F¨ op Chalmers University of Technology, Gothenburg, Sweden Ola Embr´ eus | embreus@chalmers.se 1/19
CHALMERS The runaway fluid j RE = − en RE � v � � � 1 � v � � = d p v � f RE . n RE The runaway current evolution is given by d j RE � Γ( E , t ) u ( E , t ) + d � = − ecn RE d t u ( E , t ) , d t 1 d n RE Γ( E , t ) ≡ d t , n RE u ( E , t ) ≡ � v � � / c . Ola Embr´ eus | embreus@chalmers.se 2/19
CHALMERS The runaway fluid Kinetic simulations unnecessary whenever Γ( E , t ) = Γ( E ( t )) u ( E , t ) = u ( E ( t )) , i.e. when the system is in momentaneous steady-state. 1 d j RE 1 ∂ u d E = Γ( E ) + u ( E ) ∂ E j RE d t d t Ola Embr´ eus | embreus@chalmers.se 3/19
CHALMERS The runaway fluid Requires slowly varying parameters → May be the case during the current quench τ c = 4 πε 2 0 m 2 e c 3 = m e c Collision time of relativistic electron : ln Λ n e e 4 eE c ∂ j RE /∂ t ≈ j RE ˆ j RE L Decay time of current : τ decay ∼ E c τ decay ∼ e µ 0 I RE I RE 2 π m e c ≈ 8 . 5 kA ≫ 1 τ c Ola Embr´ eus | embreus@chalmers.se 4/19
CHALMERS Example: Let’s compare time-dependent vs steady state growth rates � � 2 − 0 . 8 t E ( t ) = E c t ∆ E Ola Embr´ eus | embreus@chalmers.se 5/19
CHALMERS � � 2 − 0 . 8 t E ( t ) = E c t ∆ E × 10 − 3 5 0.85 0 � v � � /c τ c Γ -5 0.8 -10 t ∆ E = ∞ t ∆ E = ∞ -15 0.75 1.2 1.4 1.6 1.8 2 1.2 1.4 1.6 1.8 2 E/E c E/E c Ola Embr´ eus | embreus@chalmers.se 5/19
CHALMERS Self-similar evolution occurs both for growth and decay: 10 − 5 10 − 5 E = 1 . 2 E c E = 2 E c 10 − 10 d n RE / d E k d n RE / d E k 10 − 7 10 − 15 t = 0 t = 0 t = 300 τ c 10 − 20 t = 100 τ c 10 − 9 t = 600 τ c t = 200 τ c t = 900 τ c t = 300 τ c 10 − 25 0 20 40 60 80 0 20 40 60 80 Kinetic energy E k [MeV] Kinetic energy E k [MeV] Ola Embr´ eus | embreus@chalmers.se 6/19
CHALMERS � � 2 − 0 . 8 t E ( t ) = E c t ∆ E × 10 − 3 5 0.85 0 � v � � /c τ c Γ -5 t ∆ E = 10 τ c t ∆ E = 10 τ c 0.8 = 100 τ c = 100 τ c -10 = 1000 τ c = 1000 τ c = ∞ = ∞ -15 0.75 1.2 1.4 1.6 1.8 2 1.2 1.4 1.6 1.8 2 E/E c E/E c Ola Embr´ eus | embreus@chalmers.se 7/19
When quasi-steady state is valid, the mission of kinetic theory is only to determine Γ( E , ... ) (and to a lesser extent � v � � ) How do we determine Γ as accurately as possible?
CHALMERS Avalanche generation To describe knock-on collisions we add a (simplified) Boltzmann operator: d f e d t = C FP { f e } + C boltz { f e } , � � ∂σ ab C boltz { f a , f b } ( p ) = d p 1 d p 2 ∂ p v rel f a ( p 1 ) f b ( p 2 ) � d p ′ v rel σ ab ( p , p ′ ) f b ( p ′ ) − f a ( p ) Generally we can linearize ( n RE ≪ n e ) C boltz { f e , f e } ≈ C boltz { f e , f e 0 } + C boltz { f e 0 , f e } . � �� � � �� � test-particle field-particle Ola Embr´ eus | embreus@chalmers.se 9/19
CHALMERS Avalanche generation The two most established knock-on models today: C knock-on = C boltz { n e δ ( p ) , f e } (only field-particle term) 1 Rosenbluth-Putvinski: f e ( p ) = n RE lim p 2 δ ( p − p 0 ) δ ( cos θ − 1 ) p 0 →∞ Chiu-Harvey: f e ( p ) = F ( p ) δ ( cos θ − 1 ) � � � 1 F ( p ) = − 1 f e ( p ) d ( cos θ ) [Rosenbluth, Putvinski NF 1997; Chiu, Rosenbluth, Harvey NF 1998] Ola Embr´ eus | embreus@chalmers.se 10/19
CHALMERS Avalanche generation So how do these operators behave? Ola Embr´ eus | embreus@chalmers.se 11/19
CHALMERS Avalanche generation Both models have limitations: • Double counting collisions • Non-conservation of momentum and energy – Rosenbluth-Putvinski even creates infinite energy and momentum! • Chiu-Harvey model ignores pitch-angle distribution • Arbitrary cut-off affecting solutions Ola Embr´ eus | embreus@chalmers.se 12/19
CHALMERS Avalanche generation We solved this, by • Accounting for full f e ( p ) • Including the test-particle term [restores conservation laws] • Modify ln Λ in Fokker-Planck operator [avoids double counting] Ola Embr´ eus | embreus@chalmers.se 13/19
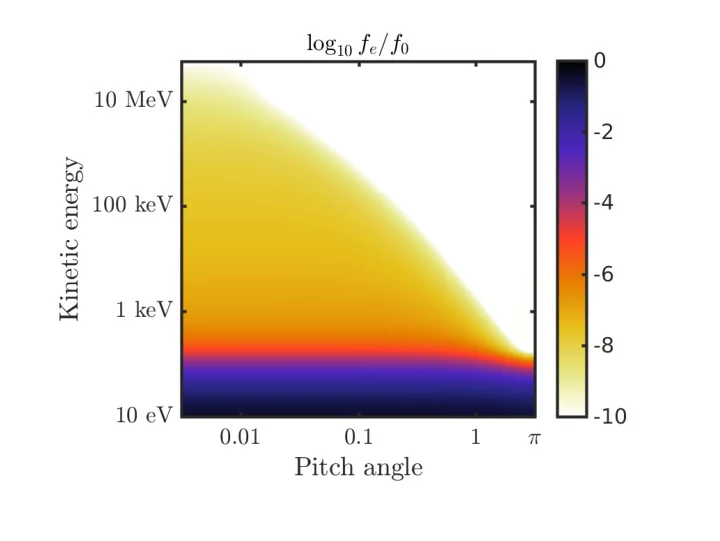
CHALMERS Avalanche generation Ola Embr´ eus | embreus@chalmers.se 14/19
CHALMERS Avalanche generation 0.045 Full Boltzmann We can now revisit a classical Field-particle Rosenbluth-Putvinski calculation [R-P , NF 1998] : E c − 1) R-P theory The steady state avalanche 0.04 growth rate Γ / ( E 1 d n RE Γ = n RE d t 0.035 0 10 20 30 E E c − 1 Ola Embr´ eus | embreus@chalmers.se 15/19
CHALMERS Avalanche generation in a near-threshold electric field An interesting situation occurs when E ∼ E c , as radiation losses become important. [P . Aleynikov and B. N. Breizman, PRL 114 , 155001 (2015)] Ola Embr´ eus | embreus@chalmers.se 16/19
CHALMERS Near-threshold electric field Approximate Γ calculated from the avalanche cross-section � γ max ∂σ Γ( E ) ≈ v ∂γ d γ. γ min Negative growth for small E : Reverse knock-ons predicted! [P . Aleynikov and B. N. Breizman, PRL 114 , 155001 (2015)] Ola Embr´ eus | embreus@chalmers.se 17/19
CHALMERS Near-threshold electric field 0.03 No avalanche • Significant reverse knock-on Full Boltzmann Aleynikov-Breizman theory however not observed in 0.02 Γ [arb. units] kinetic simulations 0.01 • Runaway decay is described mainly by Fokker-Planck 0 dynamics when Γ � 0. -0.01 1.5 2 2.5 E/E c Ola Embr´ eus | embreus@chalmers.se 18/19
CHALMERS Summary • Runaway fluids — Strictly valid when background variations slow (for example current quench) — Accuracy then only limited by the kinetics used to find Γ( E , ... ) — Runaway dissipation can be described in the fluid picture • Avalanche runaway modelling — Conservative knock-on operator from Boltzmann — Formally eliminates double counting collisions, and describes reverse knock-on Runaway kinetic theory is here to stay. Ola Embr´ eus | embreus@chalmers.se 19/19
Recommend
More recommend