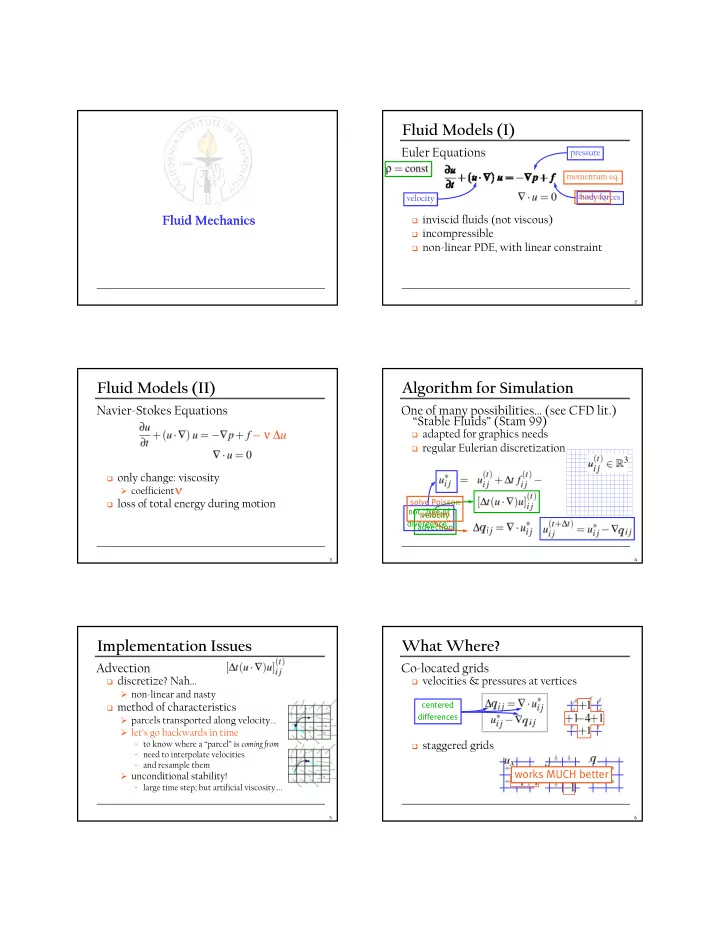
Fluid Models (I) Euler Equations pressure momentum eq. mass eq. - PDF document

Fluid Models (I) Euler Equations pressure momentum eq. mass eq. body forces velocity  inviscid fluids (not viscous) Fluid Mechanics Fluid Mechanics  incompressible  non-linear PDE, with linear constraint 2 Fluid Models (II) Algorithm for Simulation Navier-Stokes Equations One of many possibilities… (see CFD lit.) “Stable Fluids” (Stam 99)  adapted for graphics needs  regular Eulerian discretization  only change: viscosity  coefficient  loss of total energy during motion solve Poisson not “free of problem velocity divergence” advection 3 4 Implementation Issues What Where? Advection Co-located grids  discretize? Nah…  velocities & pressures at vertices  non-linear and nasty  method of characteristics centered differences  parcels transported along velocity… p p g y  let’s go backwards in time  staggered grids − to know where a “parcel” is coming from − need to interpolate velocities − and resample them works MUCH better  unconditional stability! − large time step; but artificial viscosity…. 5 6

  u   u   “Geometry” of Fluids? Geometry Revealed           u u p u u p   t t Euler equations seem clear Pressure disappears when we take the curl:  advection + div-free projection ad infinitum (vorticity)  Stam’s Stable Fluids do this wonderfully well  numerous follow-up work (Fedkiw et al. )  vorticity measures the “spin” of a parcel  but what does it mean, geometrically? , g y  vorticity is “advected” along the flow ti it i “ d t d” l th fl  “total energy” is rather unintuitive  the circulation around any  is there a notion of momentum preservation? closed loop is constant Yes  as it gets advected (by Stokes)   ( t ) u . dl  but of course, we need to massage the PDE C ( t ) − known as Kelvin’s theorem  so as to reveal the geometric structure − call it preserv. of angular momentum if you want 7 8 Geometry Revealed Towards a Proper Discretization So we know: Domain discretization = simplicial complex Integral of vorticity constant on advected sheet  fluxes through faces for velocity Additionally,  defines u  intrinsic (coordinate-free) and eulerian  if we ignore complex topology for a moment » reminiscent of staggered grids…  net flux for divergence  net flux for divergence b because u is divergence free! d f  − what comes in…must come out Vorticity is the only real variable here  flux spin for vorticity and Kelvin’s is a defining property  Torque created on a “paddle wheel” (Navier-Stokes: loss along the way)  valid for any grid… 9 10 Discrete Kelvin’s Theorem Results Guarantees circulation preservation… New method for any discrete loop!  exact discrete vorticity preservation  big loop = union of small ones  arbitrary simplicial meshes  … even on curved spaces  see also [Feldman et al. ’05, Bargteil et al ’06]  everything is intrinsic  everything is intrinsic  basic operators very simple (super parse)  great flows for small meshes!  computationally efficient even on coarse mesh  no need for millions of vortex particles  Difference with Stable Fluids?  trace back integrals, not point values 11 12

Channel Smoking Bunny 7k vertices, 32k tets; 0.45s per frame on PIV (3GHz) 13 14 Merging Vortices Movie 15 16