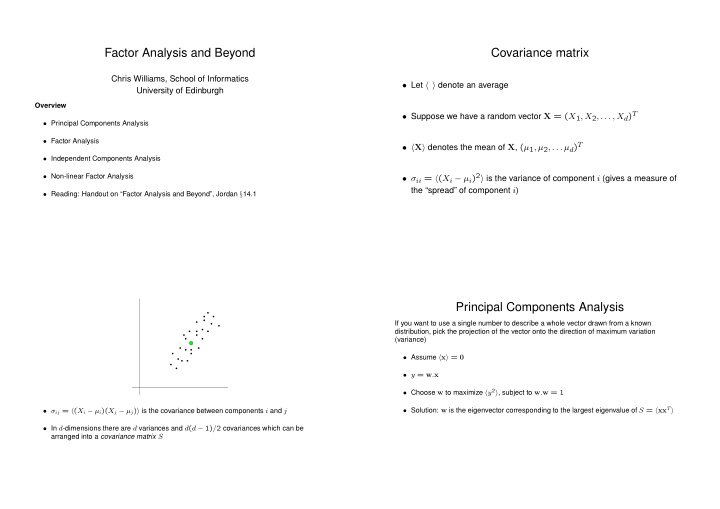



Factor Analysis and Beyond Covariance matrix Chris Williams, School of Informatics • Let � � denote an average University of Edinburgh Overview • Suppose we have a random vector X = ( X 1 , X 2 , . . . , X d ) T • Principal Components Analysis • Factor Analysis • � X � denotes the mean of X , ( µ 1 , µ 2 , . . . µ d ) T • Independent Components Analysis • σ ii = � ( X i − µ i ) 2 � is the variance of component i (gives a measure of • Non-linear Factor Analysis the “spread” of component i ) • Reading: Handout on “Factor Analysis and Beyond”, Jordan § 14.1 Principal Components Analysis . . . . . . . . If you want to use a single number to describe a whole vector drawn from a known . . . . . . . distribution, pick the projection of the vector onto the direction of maximum variation (variance) . . . . . . . . . . • Assume � x � = 0 . • y = w . x • Choose w to maximize � y 2 � , subject to w . w = 1 • Solution: w is the eigenvector corresponding to the largest eigenvalue of S = � xx T � • σ ij = � ( X i − µ i )( X j − µ j ) � is the covariance between components i and j • In d -dimensions there are d variances and d ( d − 1) / 2 covariances which can be arranged into a covariance matrix S
Factor Analysis • Generalize this to consider projection from d dimensions down to m • S has eigenvalues λ 1 ≥ λ 2 ≥ . . . λ d ≥ 0 • A latent variable model; can the observations be explained in terms of a • The directions to choose are the first m eigenvectors of S corresponding to λ 1 , . . . , λ m small number of unobserved latent variables ? • w i . w j = 0 i � = j • Fraction of total variation explained by using m principal components is • FA is a proper statistical model of the data; it explains covariance � m i =1 λ i between variables rather than variance ( cf PCA) � d i =1 λ i • PCA is basically a rotation of the axes in the data space • FA has a controversial rˆ ole in social sciences • visible variables : x = ( x 1 , . . . , x p ) , W is called the factor loadings matrix p ( x ) is like a multivariate Gaussian pancake • latent variables: z = ( z 1 , . . . , z m ) , z ∼ N (0 , I m ) • noise variables: e = ( e 1 , . . . , e p ) , e ∼ N (0 , Ψ) , where p ( x | z ) ∼ N ( W z + µ , Ψ) Ψ = diag( ψ 1 , . . . , ψ p ) . � p ( x ) = p ( x | z ) p ( z ) d z Assume p ( x ) ∼ N ( µ , WW T + Ψ) x = µ + W z + e then covariance structure of x is C = WW T + Ψ
FA example [from Mardia, Kent & Bibby, table 9.4.1] • Rotation of solution: if W is a solution, so is WR where RR T = I m as ( WR )( WR ) T = WW T . Causes a problem if we want to interpret • Correlation matrix factors. Unique solution can be imposed by various conditions, e.g. that W T Ψ − 1 W is diagonal. mechanics 1 0 . 553 0 . 547 0 . 410 0 . 389 vectors 1 0 . 610 0 . 485 0 . 437 algebra 1 0 . 711 0 . 665 analysis 1 0 . 607 statstics 1 • Is the FA model a simplification of the covariance structure? S has p ( p + 1) / 2 independent entries. Ψ and W together have p + pm free parameters (and uniqueness condition above can reduce this). FA model • Maximum likelihood FA (impose that W T Ψ − 1 W is diagonal). Require makes sense if number of free parameters is less than p ( p + 1) / 2 . m ≤ 2 otherwise more free parameters than entries in S . m = 1 m = 2 (not rotated) m = 2 (rotated) FA for visualization Variable ˜ ˜ w 1 w 1 w 2 w 1 w 2 p ( z | x ) ∝ p ( z ) p ( x | z ) 1 0.600 0.628 0.372 0.270 0.678 Posterior is a Gaussian. If z is low dimensional. Can be used for visualization (as with PCA) 2 0.667 0.696 0.313 0.360 0.673 3 0.917 0.899 -0.050 0.743 0.510 x 2 4 0.772 0.779 -0.201 0.740 0.317 o 5 0.724 0.728 -0.200 0.698 0.286 data . latent space space x = z w • 1-factor and first factor of the 2-factor solutions differ (cf PCA) . z x 1 • problem of interpretation due to rotation of factors 0
Learning W , Ψ Comparing FA and PCA • Maximum likelihood solution available (Lawley/J¨ oreskog). • Both are linear methods and model second-order structure S • EM algorithm for ML solution (Rubin and Thayer, 1982) • FA is invariant to changes in scaling on the axes, but not rotation invariant (cf PCA). – E-step: for each x i , infer p ( z | x i ) – M-step: do linear regression from z to x to get W • FA models covariance , PCA models variance • Choice of m difficult (see Bayesian methods later). Probabilistic PCA Example Application: Handwritten Digits Recognition [Tipping and Bishop (1997)] Hinton, Dayan and Revow, IEEE Trans Neural Networks 8(1), 1997 Let Ψ = σ 2 I . • Do digit recognition with class-conditional densities • 8 × 8 images ⇒ 64 · 65 / 2 entries in the covariance matrix. • In this case W ML spans the space defined by the first m eigenvectors of • 10-dimensional latent space used S • Visualization of W matrix. Each hidden unit gives rise to a weight image ... • In practice use a mixture of FAs! • PCA and FA give same results as Ψ → 0 .
Useful Texts Independent Components Analysis • A non-Gaussian latent variable model, plus linear transformation, e.g. on PCA and FA m � e −| z i | P ( z ) ∝ i =1 • B. S. Everitt and G. Dunn “Applied Multivariate Data Analysis” Edward x = W z + µ + e Arnold, 1991. • Rotational symmetry in z -space is now broken • C. Chatfield and A. J. Collins “Introduction to Multivariate Analysis”, • p ( x ) is non-Gaussian, go beyond second-order statistics of data for fitting model Chapman and Hall, 1980. • Can be used with dim( z ) = dim( x ) for blind source separation • http://www.cnl.salk.edu/~tony/ica.html • K. V. Mardia, J. T. Kent and J. M. Bibby “Multivariate Analysis”, Academic Press, 1979. Non-linear Factor Analysis � P ( x ) = P ( x | z ) P ( z ) d z For factor analysis P ( x | z ) ∼ N ( W z + µ , σ 2 I ) If we make the prediction of the mean a non-linear function of z , we get non-linear factor analysis, with P ( x | z ) ∼ N ( φ ( z ) , σ 2 I ) and φ ( z ) = ( φ 1 ( z ) , φ 2 ( z ) , . . . , φ p ( z )) T . However, there is a problem— we can’t do the integral analytically, so we need to approximate it. K P ( x ) ≃ 1 � P ( x | z k ) K k =1 where the samples z k are drawn from the density P ( z ) . Note that the approximation to P ( x ) is a mixture of Gaussians.
Fitting the Model to Data x 3 . . . φ . . . • Adjust the parameters of φ and σ 2 to maximize the log likelihood of the z 2 . . . data. z 1 x 2 • For a simple form of mapping φ ( z ) = � i w i φ i ( z ) we can obtain EM x 1 updates for the weights { w i } and the variance σ 2 . • We are fitting a constrained mixture of Gaussians to the data. The • Generative Topographic Mapping (Bishop, Svensen and Williams, 1997/8) algorithm works quite like the SOM (but is more principled as there is an objective function). Visualization + P(z|x) • The mean may be a bad summary of the z posterior distribution.
Recommend
More recommend