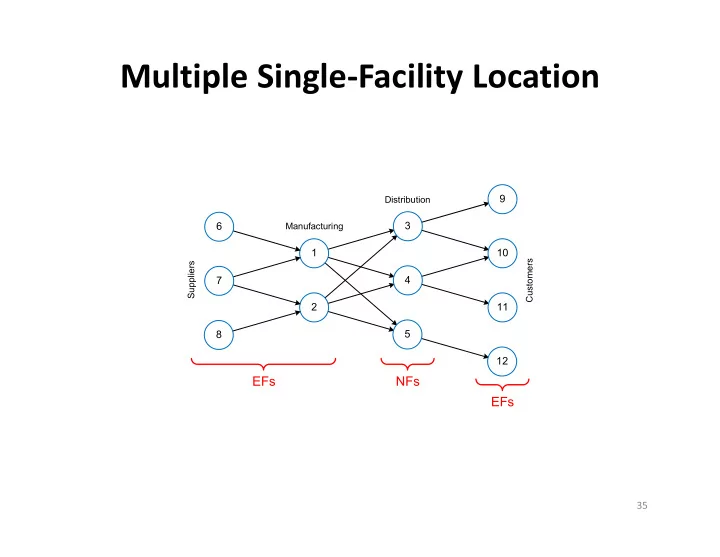
Multiple Single-Facility Location 9 Distribution 3 6 - PowerPoint PPT Presentation

Multiple Single-Facility Location 9 Distribution 3 6 Manufacturing 1 10 Customers Suppliers 7 4 2 11 5 8 12 EFs NFs EFs 35

Best Retail Warehouse Locations 36

Optimal Number of NFs TC Transport Cost 1 2 3 4 5 6 Number of NFs 37

Fixed Cost and Economies of Scale   • How to estimate facility fixed cost? β     f   =   TPC max TPC , TPC act min 0   f   – Cost data from existing facilities can be f < f   max 0 used to fit linear estimate  0.62, Hand tool mfg.  • y -intercept is fixed cost, k  0.48, Construction =  β – Economies of scale in production 0.41, Chemical processing    k > 0 and β < 1  0.23, Medical centers = + TPC k c f est p TPC TPC act 0 β − 1 = = APC f act β f f 0 TPC 0 k TPC act ( = 0.5) = + APC c est p f TPC est Actual EF cost = k fixed cost APC act APC est = c constant unit production cost p k = f / f min/max feasible scale min max TPC min c p = f Minimum Efficient Scale MES = TPC / f base cost/rate 0 0 f min f MES f 0 f max 38 Production Rate (ton/yr)

MILP [ ] = + c 6 8 max 6 x 8 x c x LP: max ' 1 2 + ≤     s.t. 2 x 3 x 11 2 3 11 1 2 ≤ s.t. Ax b = = A , b         2 0 7 ≤ 2 x 7 1 ≥ x 0 ≥ x x , 0 1 2 MILP: some x integer i 4 ILP: x integer { } ∈ BLP: x 0,1 3   1 x 3 2   2 2 , * *   ′ = = x c x 31 2 1 3   13   1 0 1 2 3 4 5 6 x 1 39

Branch and Bound [ ] + = 2 max 6 x 8 x c 6 8 1 2 UB = 31 , LB = 0 3 s.t. 2 x + 3 x ≤ 11     2 3 11 1 2 x ≤ x ≥ 3 4 A = , b =     1 1     ≤ 2 0 7 2 x 7 1 1 = = UB 31 , LB 0 ≥ 3 x x , 0 1 2 x ≤ x ≥ 1 2 x x , integer 2 2 4 1 2 UB = 31, LB = 26 30 1 x ≤ 2 3 UB = 31 , LB = 26 x ≥ 3 1 1 3 x 2 303 2 2 = = UB 30 , LB 26 31 3 2 1 313 28 x ≥ 3 x ≤ 2 2 2 2 313 1 26 2 2 = = UB 30 , LB 28 = = UB 30 , LB 30 3 3 2 <  = − gap 30 30 1 0 1 2 3 4 5 6 3 x 1 40

MILP Formulation of UFL    + min k y c x i i ij ij ∈ ∈ ∈ i N i N j M  = ∈ s.t. x 1, j M ij ∈ i N ≥ ∈ ∈ y x , i N j , M i ij ≤ ≤ ∈ ∈ 0 x 1, i N j , M ij { } ∈ ∈ y 0,1 , i N i where { } = ∈ = k fixed cost of NF at site i N 1,..., n i { } = ∈ = c variable cost from to serve EF i j M 1,..., m ij  1, if NF established at site i =  y i  0, otherwise = x fraction of EF demand served from NF at site . j i ij 41

MILP Formulation of p -Median   min c x ij ij ∈ ∈ i N j M  = s.t. y p i ∈ i N  = ∈ x 1, j M ij ∈ i N ≥ ∈ ∈ y x , i N j , M i ij ≤ ≤ ∈ ∈ 0 x 1, i N j , M ij { } ∈ ∈ y 0,1 , i N i where = p number of NF to establish { } = ∈ = c variable cost from to serve EF i j M 1,..., m ij  1, if NF established at site i =  y i  0, otherwise = x fraction of EF demand served from NF at site . j i ij 42