i A is a finite quiver Q that embeds in dimemodelw.boundanI a - PDF document

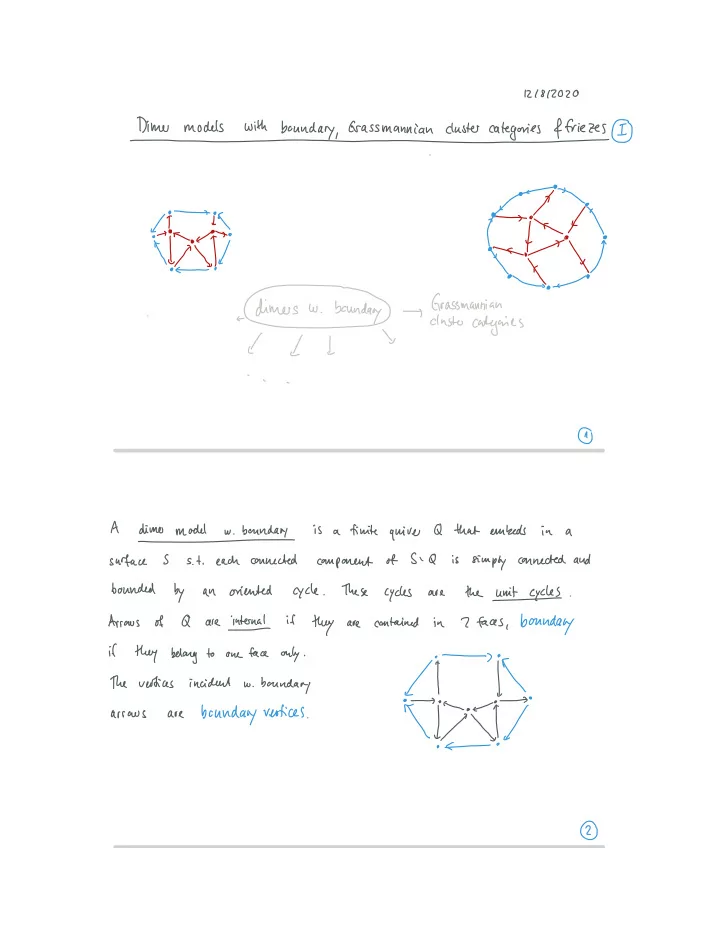
121812020 Dimemodelswithboundarydrassmanniandustercategoriesffriet Einasiumaniaigmes i A is a finite quiver Q that embeds in dimemodelw.boundanI a component of S Q surface S is simply connected and s t each connected bounded by the unicycles an oriented cycle These are cycles Arrows of if Q are internal 2 faces bounday in contained they are if belong to one face only they or µ The vertices incident w boundary o f o f boundary vertices arrows are If e

Quivers arising from Example Verdes fr diag's boundary triangulations of disks of surfaces segments arrows for rotations filings of surfaces insideD's tiles on disk Postnikovl alternating strand diagrams ortpYghna.cn q y vertices.gg k.nl diagrams on disk Scott degeneration of them ex arrows from Fent of strands a j r o o triangulations of disks of surfaces hextijaaimakadninius n It filings of surfaces I is

subset of ScottBranin on Pn I divterannadiMaiagrams Correspondences trianguisltigings ftp.lapadmeut zag paths toffee road maybe graphs P plabic graphs eta dEoiwqqk4 reduced nous amies EA I akin tiling 7 and under Images connected are reduced fully them The plabic graphs arising from flings of Pat have A black node deg a 23 t n white nodes on bdy other are blade nodes every closed face is a quadrilateral adf.edpfffateaawwqteuamddfatoao.ie Alton Sh Strand E r diagram permutation at asana grown is 5 1918 permutations dn 2 appendix by M Glick in BMartin 18 arXiv 1601.05080

emodels Algebasfrandim Q dime model i S cycles of Q w boundary the unit u E Wa rest t 5,8 WE Czt Cut Cg r iii t E For QQ basis given by all paths in Q Trivial paths b re Q vertex multiplication by concatenation of paths from idempotent trivial A a of Q clime algebra f eat ten paths atbdy vertices e Aae Ba the of Q i boundary algebra i more to this