How is Light Made? How is Light Made? Can be considered as EITHER - PDF document

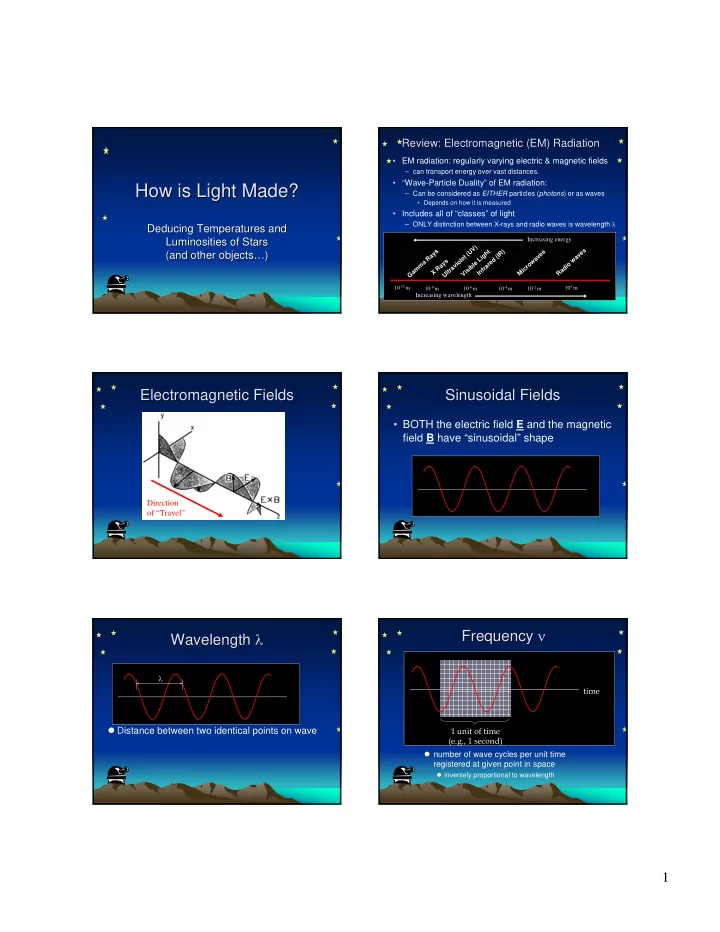
Review: Electromagnetic (EM) Radiation Review: Electromagnetic (EM) Radiation • EM radiation: regularly varying electric & magnetic fields – can transport energy over vast distances. • “Wave-Particle Duality” of EM radiation: How is Light Made? How is Light Made? – Can be considered as EITHER particles ( photons ) or as waves • Depends on how it is measured • Includes all of “classes” of light – ONLY distinction between X-rays and radio waves is wavelength λ Deducing Temperatures and Deducing Temperatures and Luminosities of Stars Increasing energy Luminosities of Stars ) V s s U t ) s (and other objects… …) ) y h R e (and other objects ( e a g v t I v R i ( a e L a d w s l w a o e e y o m i l r o a v b a r i m R a r c d i r s f i a a X t n M l V i R G U I 10 -15 m 10 3 m 10 -9 m 10 -6 m 10 -4 m 10 -2 m Increasing wavelength Electromagnetic Fields Electromagnetic Fields Sinusoidal Fields Sinusoidal Fields • BOTH the electric field E and the magnetic field B have “sinusoidal” shape Direction of “Travel” ν Frequency ν Wavelength λ λ Frequency Wavelength λ time � Distance between two identical points on wave 1 unit of time (e.g., 1 second) � number of wave cycles per unit time registered at given point in space � inversely proportional to wavelength 1

“Units “ Units” ” of Frequency of Frequency Wavelength and Frequency Wavelength and Frequency λ = v /ν = c /ν (in vacuum) ⎡ ⎤ meters c ⎢ ⎥ ⎡ ⎤ ⎣ ⎦ = cycles second ν � Proportional to Velocity v ⎢ ⎥ ⎡ ⎤ ⎣ ⎦ � Inversely proportional to temporal frequency ν meters second λ ⎢ ⎥ � Example: ⎣ ⎦ cycle � AM radio wave at ν = 1000 kHz = 10 6 Hz ⎡ ⎤ = � λ = c/ ν = 3 × 10 8 m/s / 10 6 Hz = 300 m cycle 1 1 "Hertz" (Hz) ⎢ ⎥ � λ for AM radio is long because frequency is small ⎣ ⎦ second Generating Light Generating Light Light as a Particle: Photons Light as a Particle: Photons � Photons: little “packets” of energy • Light is generated by converting one class � Energy is proportional to frequency of energy to electromagnetic energy E = h ν – Heat – Explosions Energy = (Planck’s constant) × (frequency of photon) h ≈ 6.625 × 10 -34 Joule-seconds = 6.625 × 10 -27 Erg-seconds Planck’ Planck ’s Radiation Law s Radiation Law Converting Heat to Light Converting Heat to Light The Planck Function The Planck Function • Wavelength of MAXIMUM emission λ max • Every opaque object (a human, a planet, a star) radiates a characteristic spectrum of EM radiation is characteristic of temperature T – Spectrum: Distribution of intensity as function of wavelength • Wavelength λ max ↓ as T ↑ – Distribution depends only on object’s temperature T • Blackbody radiation ultraviolet visible infrared radio As T ↑ , λ max ↓ Intensity (W/m 2 ) 0.1 1.0 10 100 1000 10000 λ max http://scienceworld.wolfram.com/physics/PlanckLaw.html 2

Temperature dependence Temperature dependence Sidebar: The Actual Equation Sidebar: The Actual Equation of blackbody radiation of blackbody radiation • As object’s temperature T increases : 2 2 hc 1 ( ) 1. Wavelength of maximum of blackbody spectrum (Planck = B T function) becomes shorter (photons have higher energies) λ hc 5 − 2. Each unit surface area of object emits more energy (more e λ kT 1 photons) at all wavelengths • Derived in Solid State Physics • Complicated!!!! (and you don’t need to know it!) h = Planck’s constant = 6.63 × 10 -34 Joule - seconds k = Boltzmann’s constant = 1.38 × 10 -23 Joules per Kelvin c = velocity of light = 3 × 10 +8 meter - second -1 Planck Curve for T = 7000- -K K Shape of Planck Curve Shape of Planck Curve Planck Curve for T = 7000 http://csep10.phys.utk.edu/guidry/java/planck/planck.html http://csep10.phys.utk.edu/guidry/java/planck/planck.html • This graph is also “normalized” to 1 at maximum • “Normalized” Planck curve for T = 5700K • Maximum intensity occurs at shorter wavelength λ – Maximum Intensity set to 1 • Note that maximum intensity occurs in visible region of – boundary of ultraviolet (UV) and visible spectrum for T = 5700K Two Planck Functions Two Planck Functions Features of Graph of Planck Law Features of Graph of Planck Law Displayed on Logarithmic Scale Displayed on Logarithmic Scale T 1 T 1 < T < T 2 (e.g., T 1 = 5700K, T 2 = 7000K) 2 (e.g., T 1 = 5700K, T 2 = 7000K) • Maximum of curve for higher temperature occurs at SHORTER wavelength λ : – λ max (T = T 1 ) > λ max (T = T 2 ) if T 1 < T 2 • Curve for higher temperature is higher at ALL WAVELENGTHS λ ⇒ More light emitted at all λ if T is larger – Not apparent from normalized curves, must http://csep10.phys.utk.edu/guidry/java/planck/planck.html • Graphs for T = 5700K and 7000K displayed on examine “unnormalized” curves, usually on logarithmic scale same logarithmic scale without normalizing – Note that curve for T = 7000K is “higher” and its peak is farther “to the left” 3

Wavelength of Maximum Emission Wavelength of Maximum Emission Colors of Stars Colors of Stars Wien’ ’s s Displacement Law Displacement Law Wien • Star “Color” is related to temperature – If star’s temperature is T = 5000K, the wavelength • Obtained by evaluating derivative of Planck of the maximum of the spectrum is: Law over temperature T × − × − 3 2 . 898 10 3 [ ] 2.898 10 λ = ≅ µ = λ = m 0 . 579 m 579 nm meters [ ] max 5000 max T K Human vision range (in the visible region of the spectrum, green) 400 nm = 0.4 µ m ≤ λ ≤ 700 nm = 0.7 µ m (1 µ m = 10 -6 m) Colors of Stars Colors of Stars Blackbody Curve for T=3000K Blackbody Curve for T=3000K • If T << 5000 K (say, 2000 K), the wavelength of the maximum of the spectrum is: − × 3 2 . 898 10 λ = ≅ µ ≅ m 0 . 966 m 966 nm max 3000 (in the “near infrared” region of the spectrum) • The visible light from this star appears “reddish” • In visible region, more light at long λ – Why? ⇒ Visible light from star with T=3000K appears “reddish” Colors of Stars Colors of Stars Colors of Stars Colors of Stars • Color of star indicates its temperature • If T << 5000 K (say, 2000 K), the wavelength of – If star is much cooler than 5,000K, the the maximum of the spectrum is: maximum of its spectrum is in the infrared and the star looks “reddish” − × 3 2 . 898 10 λ = ≅ µ ≅ m 1 . 449 m 1450 nm • It gives off more red light than blue light max 2000 – If star is much hotter than 15,000K, its spectrum peaks in the UV, and it looks “bluish” (peaks in the “near infrared” region of the spectrum) • It gives off more blue light than red light 4

Planck Curves for Planck Curves for Betelguese and and Rigel Rigel in Orion in Orion Betelguese Rigel Rigel and Betelgeuse and Betelgeuse Betelgeuse: 3,000 K (a red supergiant ) RIgel Betelgeuse Rigel: 30,000 K (a blue supergiant ) Plotted on Log-Log Scale to “compress” range of data Luminosities of stars Luminosities of stars Luminosities of stars Luminosities of stars • Sum of all light emitted over all wavelengths • Stefan-Boltzmann Law is the luminosity = σ 4 L T – A measure of “power” ( watts ) – Measures the intrinsic brightness instead of apparent brightness that we see from Earth L = Power emitted per unit surface area • Hotter stars emit more light at all wavelengths σ = Stefan-Boltzmann Constant through each unit area of its surface ≈ 5.67 × 10 -8 Watts / (m 2 K 4 ) – luminosity is proportional to T 4 ⇒ small increase in • Obtained by integrating Planck’s Law over λ temperature makes a big increase in luminosity • Luminosity is proportional to T 4 ⇒ small increase in temperature produces big increase in luminosity Consider 2 stars with same Consider 2 stars with same What about large & small stars What about large & small stars diameter and different T’ ’s s with same temperature T? diameter and different T with same temperature T? • Surface Area of Sphere ∝ R 2 – R is radius of star • Two stars with same T, different luminosities – the more luminous star must be larger to emit more light 5