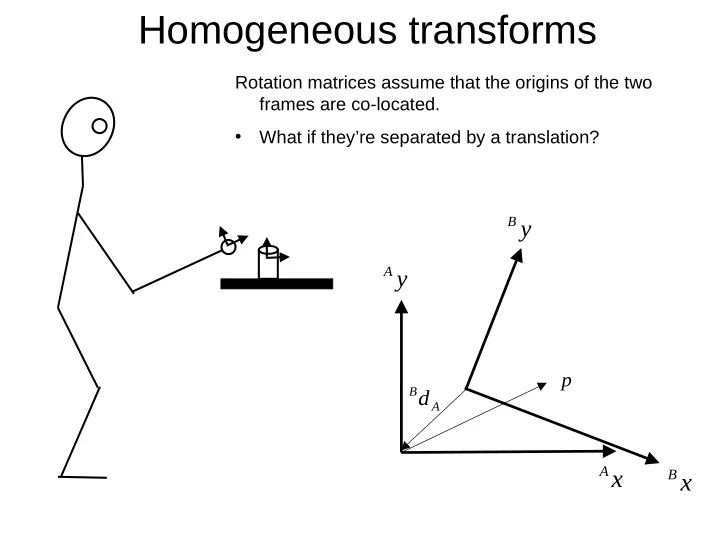
Homogeneous transforms Rotation matrices assume that the origins of - PowerPoint PPT Presentation

Homogeneous transforms Rotation matrices assume that the origins of the two frames are co-located. • What if they’re separated by a translation? B y A y p B d A A x B x

Homogeneous transform B ˆ y A ˆ y (same point, two reference frames) B p A d B A p A ˆ B ˆ x x A A B A = + p R p d B B

Homogeneous transform B y A A B A = + p R p d A y B B     A A B R d p p     = B B a d     b 0 1 1     A x B   A x r r r d   11 12 13 x     A B B  r r r d  p p     A = 21 22 23 y = T       B A r r r d 1 1       31 32 33 z   0 0 0 1   always one always zeros

Example 1: homogeneous transforms B x B y B z l A y θ A x A z B T What’s ? A

Example 1: homogeneous transforms A y B T What’s ? B B y x A θ θ − θ  cos( ) sin( ) 0  A x   A , A R = θ θ sin( ) cos( ) 0 z B z   B   0 0 1   − l    B B R d     B = A A T B B = x d A 0     B A y 0 1     0 B z   l θ θ − cos( ) sin( ) 0 l     − θ θ sin( ) cos( ) 0 0   A y B = T A   0 0 1 0   θ   0 0 0 1   A x A z

Example 2: homogeneous transforms y x z ( ) b   θ − θ θ + c 0 s l 2 c π b b 4   ( ) θ θ θ + s 0 c l 2 s π   a = T b 4 l   − 0 1 0 0    0 0 0 1    l y z This arm rotates about the axis. a a θ x a z a a T What’s ? b

Example 3: homogeneous transforms A ˆ y c ˆ c ˆ y x l c ˆ z φ θ A ˆ x A ˆ z   − − c 0 s c s 0 c c s c s       θ θ φ φ θ φ φ θ θ     a = a b = = R R R 0 1 0 s c 0  s c 0      φ φ φ φ c b c       − − s 0 c 0 0 1 s c s s c       θ θ θ φ θ φ θ

Example 3: homogeneous transforms A ˆ y c ˆ c ˆ y x l c ˆ z φ θ A ˆ x A ˆ z − l   −  −   c c s c s l lc c     θ φ φ θ θ   θ φ    c = d 0 a a c =− = − = d R d s c 0 0 ls         c φ φ φ         0 − − s c s s c 0 ls c         θ φ θ φ θ θ φ − c c s c s lc c   θ φ φ θ θ θ φ     a a s c 0 ls R d     φ φ φ a c = = T     c − − s c s s c ls c 0 1     θ φ θ φ θ θ φ   0 0 0 1  

Inverse of the Homogeneous transform Can also derive it from the forward Homogeneous transform: B = B A + B p R p d A A ( ) T A B B B = − p R p d A A   B p − 1   A B = p T   A 1     T T B B B − R R d −   1 B = where A A A T   A 0 1  

Inverse of the Homogeneous transform B ˆ y A ˆ y (same point, two reference frames) B p A d B A p A ˆ B ˆ x x ( ) B B A B A B A A = − = − p R p R d R p d A A B A B

Example 1: homogeneous transform inverse B x B y B z l θ θ −  cos( ) sin( ) 0 l    − θ θ sin( ) cos( ) 0 0   B = T A   A y 0 0 1 0     0 0 0 1   θ A x A T What’s ? B A z

Example 1: homogeneous transform inverse θ − θ cos( ) sin( ) 0     T T B B B − R R d   − 1   B = T A A A A R = θ θ sin( ) cos( ) 0     B A   0 1   0 0 1   − θ − θ − θ l  cos( ) sin( ) 0 l l cos( )              B A B = − = θ θ = θ d A 0 R d sin( ) cos( ) 0 0 l sin( )         B A         0 0 0 1 0 0         θ − θ θ  cos( ) sin( ) 0 l cos( )    θ θ θ sin( ) cos( ) 0 l sin( )   − 1 B A = = T T   A B 0 0 1 0     0 0 0 1  

Example 2: homogeneous transform inverse y x z ( ) b   θ − θ θ + c 0 s l 2 c π b b 4   ( ) θ θ θ + s 0 c l 2 s π   a = T b 4 l   − 0 1 0 0    0 0 0 1    b T What’s ? a l y ( ) a   θ θ − + c s 0 l 2 c c s s θ θ π π θ θ + θ +   4 4 − 0 0 1 0   x b = ( ) T a   a − θ θ − s c 0 l 2 s c c s z θ π θ π  θ + θ +  4 4 a 0 0 0 1    

Forward Kinematics • Where is the end effector w.r.t. the “base” frame?

Composition of homogeneous transforms 3 x Base to eff transform 3 y l 3 l 0 0 1 2 T = T T T q 2 3 2 3 1 2 3 x 1 x 1 y q 2 Transform associated w/ link 3 2 y 0 y Transform associated w/ link 2 q 1 0 x l Transform associated w/ link 1 1 0 z

Forward kinematics: composition of homogeneous transforms 3 x 0 0 1 2 T = T T T 3 1 2 3 −  c s 0 l c  3 y 1 1 1 1   s c 0 l s   l 1 1 1 1 0 = T 3   1 0 0 1 0 l q   2 3 2   x 1 x 0 0 0 1   1 y q −  c s 0 l c  2 2 2 2 2   s c 0 l s   2 2 2 2 1 = T 2 y   0 2 y 0 0 1 0     0 0 0 1   q 1 0 x l 1 0 z

Forward kinematics: composition of homogeneous transforms 3 x 0 0 1 2 T = T T T 3 1 2 3 3 y − c s 0 l c   3 3 3 3   l s c 0 l s   3 3 3 3 3 2 = T   l q 3 0 0 1 0 2 3 2 x   1 x   1 0 0 0 1 y   q 2 2 y 0 y q 1 0 x l 1 0 z

Remember those double-angle formulas… ( ) ( ) ( ) ( ) ( ) θ ± φ = θ φ ± θ φ sin sin cos cos sin ( ) ( ) ( ) ( ) ( ) θ ± φ = θ φ  θ φ cos cos cos sin sin

Forward kinematics: composition of homogeneous transforms 0 0 1 2 T = T T T 3 1 2 3 − − − c s 0 l c c s 0 l c c s 0 l c       1 1 1 1 2 2 2 2 3 3 3 3       s c 0 l s s c 0 l s s c 0 l s       1 1 1 1 2 2 2 2 3 3 3 3 0 = T       3 0 0 1 0 0 0 1 0 0 0 1 0             0 0 0 1 0 0 0 1 0 0 0 1       − + + c s 0 l c l c l c   123 123 1 1 2 12 3 123   + + s c 0 l s l s l s   123 123 1 1 2 12 3 123 0 = T   3 0 0 1 0     0 0 0 1  

DH parameters • There are a large number of ways that homogeneous transforms can encode the kinematics of a manipulator • We will sacrifice some of this flexibility for a more systematic approach: DH (Denavit-Hartenberg) parameters. • DH parameters is a standard for describing a series of transforms for arbitrary mechanisms. 3 3 x z 3 x 3 y l l 3 3 2 x l q 2 l 3 2 q x 1 x 2 3 1 1 y z 2 z q 2 q 2 1 2 x y 0 y 0 y q 1 q 0 x 1 l 0 1 z l 0 1 z 0 x

Forward kinematics: DH parameters These four DH parameters, ( ) α θ a d i i i i represent the following homogeneous matrix: − c s 0 0 1 0 0 0 1 0 0 a 1 0 0 0         θ θ i         i i − s c 0 0 0 1 0 0 0 1 0 0 0 c s 0         θ θ α α = T i i i i         0 0 1 0 0 0 1 d 0 0 1 0 0 s c 0         α α i i i         0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1         a d Then, translate by along x axis First, translate by along z axis i i α θ and rotate by about x axis and rotate by about z axis i i