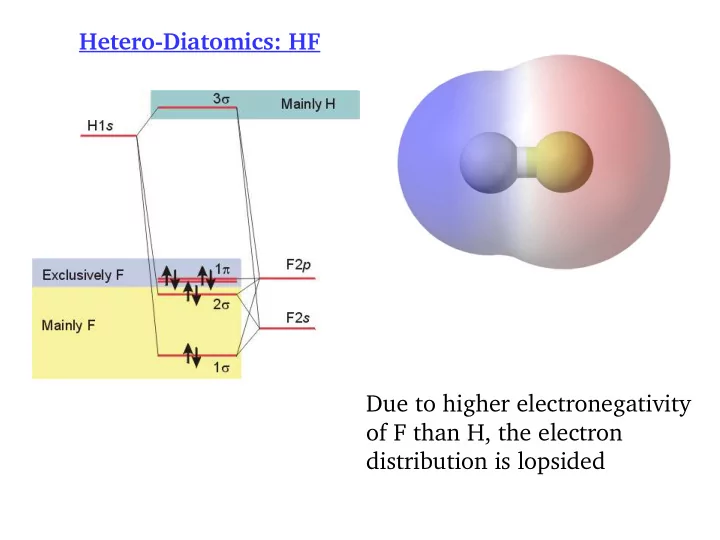
Hetero-Diatomics: HF Due to higher electronegativity of F than H, - PowerPoint PPT Presentation

Hetero-Diatomics: HF Due to higher electronegativity of F than H, the electron distribution is lopsided

Hetero-Diatomics: HCl For Cl 3p states close in energy to the 1s of H

Hetero-Diatomics: HBr For Cl 4p states close (higher) in energy to the 1s of H

Hetero-Diatomics: CO

Hybridization Linear combination of atomic orbitals within an atom leading to more effective bonding 2pz 2px 2py 2px 2py α 2s- β 2pz α 2s+ β 2pz 2s The coefficients α and β depend on field strength Hybridization is close to VBT approach. Use of experimental information All hybridized orbitals are equivalent and are ortho-normal to each other

s+p (sp)Hybridization 2 equivalent hybrid orbitals of the same energy and s and p orbital of the Same atom! shape (directions different) Not same as S (overlap) 1   ψ = ψ + ψ   2 s p 2 1   ψ = ψ − ψ   1 s p 2 Linear geometry with Hybridized atom at the center Contribution from s =0.5; contribution from p =0.5 Have to normalize each hybridized orbital

s+p (sp)Hybridization

s+p (sp)Hybridization The other p-orbitals are available for π bonding

Molecular orbitals of BeH2

Molecular orbitals of BeH2 ( ) ϕ = ψ − ψ − ψ u * Be H H c c A B pz σ 4 2 3 1 s 1 s ( ) ϕ = ψ − ψ + ψ H H g * Be c c A B s σ 2 2 1 1 s 1 s ( ) ϕ = ψ + ψ − ψ u Be H H c c A B pz σ 3 2 4 1 s 1 s ( ) ϕ = ψ + ψ + ψ g Be H H c c A B s σ 1 2 2 1 s 1 s

Molecular orbitals & Hybridization in BeH2 ( ) ϕ = ψ + ψ − ψ H H u Be c c A B pz σ 3 2 4 1 s 1 s ϕ + ϕ ϕ − ϕ g u g u ( ) σ σ σ σ ϕ = ψ + ψ + ψ H H g Be c c A B s σ 1 2 2 1 s 1 s

s+2p (sp2)Hybridization px and py can be combined with s to get three 3 equivalent hybrids at 120o to each other y y y 30o 30o 30o x x x 30o 30o 30o − + cos(60) cos(30) s p p + s p x y x − − cos(60) cos(30) s p p x y

s+2p (sp2)Hybridization 1 2 ψ = ψ + × ψ + ψ 0 1 s px py 3 3 1 1 1 ψ = ψ + ψ − ψ 2 s px py 3 2 6 1 1 1 ψ = ψ − ψ − ψ 3 s px py 3 2 6 The other p-orbital are available for π bonding

s+2p (sp2)Hybridization

s+3p (sp3)Hybridization 1 1 1 1 ψ = ψ + ψ + ψ + ψ 1 s px py pz 2 2 2 2 1 1 1 1 ψ = ψ − ψ − ψ + ψ 2 s px py pz 2 2 2 2 1 1 1 1 ψ = ψ + ψ − ψ − ψ 3 s px py pz 2 2 2 2 1 1 1 1 ψ = ψ − ψ + ψ − ψ 4 s px py pz 2 2 2 2 1 3 ψ = ψ + × ψ + × ψ + ψ 0 0 1 s px py pz 2 2 How to calculate the coefficients? 1 2 1 ψ = ψ + ψ + × ψ − ψ 0 2 s px py pz Use orthogonality of hybrid orbitals 2 3 2 3 and normalization conditions 1 1 1 1 ψ = ψ − ψ + ψ − ψ 3 s px py pz There is no unique solution 2 6 2 2 3 1 1 1 1 ψ = ψ − ψ − ψ − ψ 4 s px py pz 2 6 2 2 3

s+3p (sp3)Hybridization No other p-orbital is available for π bonding

Asymmetrical Hybridization: Water Molecule Electronic Configuration of ‘O’ atom: 1s22s22pz22px12py1 φ = + ψ = + + 1 2 ( ) 2 2 2 c s c p O a s a p a p 1 1 2 1 1 2 3 H xO x y A ψ = + + φ = + ( ) 2 2 2 1 2 O a s a p a p c s c p 2 4 5 6 2 3 4 x y H yO B 104.5o ψ = × + × + × ( ) 0.45 2 0.71 2 0.55 2 O s p p 1 x y ψ = × − × + × ( ) 0.45 2 0.71 2 0.55 2 O s p p 2 x y

Asymmetrical Hybridization: Water Molecule Electronic Configuration of ‘O’ atom: 1s22s22pz22px12py1 ψ = × + × + × ( ) 0.45 2 0.71 2 0.55 2 O s p p 1 x y Form bonds with ψ = × − × + × ( ) 0.45 2 0.71 2 0.55 2 O s p p two Hydrogen atoms 2 x y ψ = × − × ( ) 0.77 2 0.63 2 O s p 3 y ψ = Two lone pair electrons ( ) 2 O p 4 z

Asymmetrical Hybridization: Water Molecule Electronic Configuration of ‘O’ atom: 1s22s22pz22px12py1 ψ = × + × + × ( ) 0.45 2 0.71 2 0.55 2 O s p p 1 x y Form bonds with ψ = × − × + × ( ) 0.45 2 0.71 2 0.55 2 O s p p two Hydrogen atoms 2 x y ψ = × − × ( ) 0.77 2 0.63 2 O s p 3 y ψ = Two lone pair electrons ( ) 2 O p 4 z NOT Equivalent!

Asymmetrical Hybridization: Water Molecule Electronic Configuration of ‘O’ atom: 1s22s22pz22px12py1 ψ = × + × + × ( ) 0.45 2 0.71 2 0.55 2 O s p p Form bonds with 1 x y two Hydrogen atoms ψ = × − × + × ( ) 0.45 2 0.71 2 0.55 2 O s p p 2 x y ψ = × − × ( ) 0.77 2 0.63 2 O s p 3 y Two lone pair electrons ψ = ( ) 2 O p 4 z NOT Equivalent! 104.5o ψ = × − × + × ( ) 0.55 2 0.45 2 0.71 2 O s p p 3 y z ψ = × − × − × ( ) 0.55 2 0.45 2 0.71 2 O s p p 4 y z

Asymmetrical Hybridization: Water Molecule ψ = × + × + × ( ) 0.45 2 0.71 2 0.55 2 O s p p Form bonds with 1 x y ψ = × − × + × ( ) 0.45 2 0.71 2 0.55 2 O s p p two Hydrogen atoms 2 x y ψ = × − × + × ( ) 0.55 2 0.45 2 0.71 2 O s p p 3 y z Lone pair electrons ψ = × − × − × ( ) 0.55 2 0.45 2 0.71 2 O s p p 4 y z Lone pair electrons have more ‘ s ’ character than the bonding orbitals

Asymmetrical Hybridization: Water Molecule ψ = × + × + × ( ) 0.45 2 0.71 2 0.55 2 O s p p 1 x y Bond pairs ψ = × − × + × ( ) 0.45 2 0.71 2 0.55 2 O s p p 2 x y ψ = × − × + × ( ) 0.55 2 0.45 2 0.71 2 O s p p 3 y z Lone pairs ψ = × − × − × ( ) 0.55 2 0.45 2 0.71 2 O s p p 4 y z 0.55 0.55 0.71 0.71 θ =104.47 -1 (0.55/0.71) θ '=tan =37.76 -1.0 -0.5 0.0 0.5 1.0

s-p3-d2 & s-p3-d Hybridization Sp3d2 Octahedral Sp3d Trignoal bipyramidal

Hybridization and Geometry

Do Orbitals Really Exist? Tomographic image of HOMO of N2 Nature; Volume 342; Year 2004; 867-871