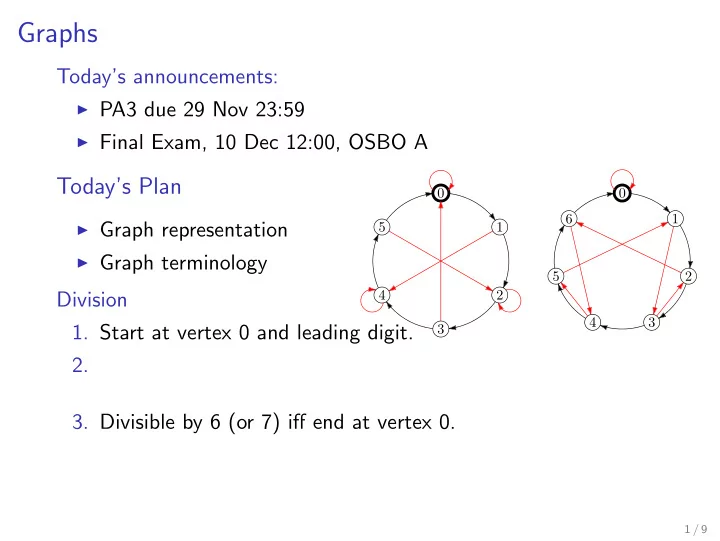
Graphs Todays announcements: PA3 due 29 Nov 23:59 Final Exam, 10 - PowerPoint PPT Presentation

Graphs Today’s announcements: ◮ PA3 due 29 Nov 23:59 ◮ Final Exam, 10 Dec 12:00, OSBO A Today’s Plan 0 0 6 1 ◮ Graph representation 5 1 ◮ Graph terminology 5 2 Division 4 2 4 3 1. Start at vertex 0 and leading digit. 3 2. 3. Divisible by 6 (or 7) iff end at vertex 0. 1 / 9

MYTH Greek gods Graph of greek mythological figures CHAOS t i e s d e i d i a l U S m o r E R E B p r i E R O S N Y X G A E A P O N T U S S N M E E S I C E R M O R O S H N A A T S O A E A T H E R T U R A H E M E R N U S A N S T I T H E A I T A P E T U O N S H Y P E R I O Y S N E C O M N E M N E A N U S T E T Y H S T E H M I S C O E U S E U R Y P H O E B E L N E E B I A C R E U S D I O N E S E R H E A C O R N O S I O S E H L N P R O O S E E R U S M E H T E E U S T H A U M A S E R S E D P O R I S L E T O M E T I S P A L L A S E R S I S T Y X I N C A H U S M L E I A H D A E S P O S E D I O N H E R A Z E U S H E S T I A S E P L E I A G O N E E L E O D C T R A S T Y S & N X R C E y m p C I h s P A H E D E M E T E R P A S I S R E S P E I A N S O L Y M P T W E L V E K A T H E O N - S E S D O D E M U C H A R O N C L Y M N E A R O I N P E R S P E H O N E G A L A T E L I O P E A P C A L R O T O I T E C L I O A G A H E B E A R E S A T H E N A A P H R O D H L A I A V E A M A N A I T P H I T R I T E E U R R I I S S D I K B I A O A R T E M I N I K E A P O L L A T E I O A T H R A U S L A S S T I U S O E A G R T H E U S A C R I S I A G E N O R E T L P E H Y C R E E N A S S A A R E U S M A T Y N D B R O S T I R O T N I A E L D E A U O D R A M A P H E U S P H I A O R Y T O E Y R T H E A P H O E N X I E U H E S P E R O P A R O M U L U S R E M U S D S R I A I G O E D E M A L C E M N E N S & D A N E A U M A H D O I M E D S E H R A M O N I A C A S T O R A U S M E N E L L E N S H E H R E A C E L E P R S E U S M L E E D R Y O E P H E R M S E M N I O S S E O N E H E R M I S S Y M A E T H I S D I O N Y S U P A N A R A I D N E A C I S L A T R A M Y S LEGEND OF THE MYTH FAMILY IN THE MYTH FATHER MOTHER ZEUS Zeus CHILDREN D E M E M I S E E T R H E R A L E O T T H M A A I D I O E N S E M L E E COLORS IN THE MYTH PRIMORDIAL DEITIES TITANS SEA GODS AND NYMPHS DODEKATHEON, THE TWELVE OLYMPIANS OTHER GODS P E R S P E H O N D K I E E H E B E A R L L O A R E T M I S MUSES E S H E R M E S A T H E N A P A H R O I D T E D I O N Y S U S A P O E U R O P GODS OF THE UNDERWORLD A A D N A E S Y N E L A C E M E N E L E D A M N E M O ANIMALS AND HYBRIDS HUMANS AND DEMIGODS circles in the myth 196 M - 8690 K { Google results } M N I O S L I O P E 8690 K - 2740 K P R E S E U S H E R A C H T A L I A C L I O C A L L E S H E E L N U R A N I A 2740 K - 1080 K 1080 K - 2410 2 / 9 J. KLAWITTER & T . MCHEDLIDZE

Graph definition A graph is a pair of sets: G = ( V , E ). ◮ V is a set of vertices: { v 1 , v 2 , . . . , v n } . ◮ E is a set of edges: { e 1 , e 2 , . . . , e m } where each e i is a pair of vertices: e i ∈ V × V . A C V = { A , B , C } B E = { ( A , B ) , ( B , A ) , ( C , B ) } If each edge is an ordered pair (i.e. ( A , B ) � = ( B , A )) then the graph is directed otherwise undirected . 3 / 9

Graph Applications Storing things that are graphs by nature ◮ Road networks ◮ Airline flights ◮ Relationships between people, things ◮ Room connections in Hunt the Wumpus Compilers ◮ call graph - which functions call which others ◮ control flow graph - which fragments of code can follow which others ◮ dependency graphs - which variables depend on which others Others ◮ circuits, class hierarchies, meshes, networks of computers, ... 4 / 9

Graph vocabulary Vertices adjacent to v : N ( v ) = { u | ( u , v ) ∈ E } b a c Edges incident to v : I ( v ) = { ( u , v ) | u ∈ N ( v ) } 8 9 e d g f 6 7 Degree of v : deg( v ) = | I ( v ) | o n m 4 5 l Path: Sequence of vertices connected by edges j k 2 3 i Cycle: Path with same start and end vertex h 0 1 q p Simple graph: No self-loops or multi-edges 5 / 9

Graph vocabulary Subgraph of G = ( V , E ): ( V ′ ⊆ V , E ′ ⊆ E ) and if ( u , v ) ∈ E ′ then u , v ∈ V ′ b a c 8 9 e d Complete graph: Maximum number of edges g f 6 7 o Connected graph: Path between every pair of n m vertices 4 5 l j k 2 3 Connected component: Maximal connected i subgraph h 0 1 q p Acyclic graph: no cycles Spanning tree of G ( V , E ): Acyclic, connected graph with vertex set V 6 / 9

Graph Vocabulary b 1. List the edges incident to vertex b : a c 2. What is the degree of vertex d ? 8 9 e 3. List the vertices adjacent to vertex i : d 4. Give a path from 0 to 7: g f 6 7 o 5. Give a path from k to h : n m 4 5 6. Vertices in the largest complete subgraph in G : l 7. How many connected components are in G ? j k 2 3 8. How many edges in a spanning forest? i h 9. How many simple paths connect 0 and 9? 0 1 q p 10. Can you draw G with no edge crossings? 7 / 9

Number of edges How many edges in a simple connected graph on n vertices? Minimum Maximum 1. If n = 1 or 2, minimally connected has edges. 2. IH: minimally connected on n − 1 vertices has edges. 3. Minimally connected graphs are acyclic. 4. If deg( v ) ≥ 2 for all v ∈ V then graph has cycle. 5. So minimally connected graph contains v with deg( v ) = 1. 6. Remove this v (and one incident edge). 7. Remaining graph is min. conn. and has edges (by IH). 8. Original n vertex graph has edges. How many edges in a non-simple, non-connected graph on n vertices? Minimum Maximum 8 / 9

Handshaking Theorem: If G = ( V , E ) is an undirected graph, then � deg( v ) = 2 | E | v ∈ V Corollary An undirected graph has an even number of vertices of odd degree. 9 / 9